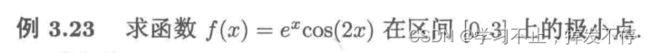Python在高等数学和线性代数中的应用

Python数学实验与建模学习

目录

1. SymPy工具库

1.1 符号运算基础

1.2 用SymPy做符号函数画图

 2. 高等数学的符号解

2.1 极限

2.2 导数 

2.3 级数求和 

2.4 泰勒展开 

2.5 不定积分和定积分 

2.6 代数方程 

2.7 微分方程 

3. 高等数学问题的数值解

3.1 一重积分

3.1.1 梯形计算

3.1.2 辛普森计算

3.2 多重积分

3.3 非线性方程数值解

3.3.1 二分法求根

3.3.2 牛顿迭代法求根

3.3.3 scipy工具库求解

 3.4 极值点的数值解

3.4.1 一元函数

3.4.2 多元函数

4. 线性代数的符号解和数值解

4.1 线性方程组

4.2 齐次线性方程组 nullspace

4.3 非齐次线性方程

4.4 特征值与特征向量

4.5 可逆矩阵与对角阵

---

1. SymPy工具库

1.1 符号运算基础

使用SymPy库进行符号计算，首先要建立符号变量及符号表达式。符号变量可以通过库中的symbols()创建。创建多个变量时以空格分隔。也可以将m0：3传入符号函数，生成如m0,m1,m2的符号序列，定义符号变量。

在符号计算中，可以使用evalf()或者n()的方法来获得任何对象的浮点近似值。subs()方法代入值示例如下：

from sympy import *
x,y,z=symbols('x  y  z')
m0,m1,m2,m3=symbols('m0:4')  #创建多个符号变量
x=sin(1)
print("x=",x); 
print("x=",x.evalf())
print("x=",x.n(16))  #显示小数点后16位数字
print("pi的两种显示格式:{},{}".format(pi,pi.evalf(3)))  #这里不能使用n()函数
expr1=y*sin(y**2)  #创建第一个符号表达式
expr2=y**2+sin(y)*cos(y)+sin(z)  #创建第二个符号表达式
print("expr1=",expr1)
print("y=5时，expr1=",expr1.subs(y,5))  #代入一个符号变量的值
print("y=2,z=3时，expr2=",expr2.subs({y:2,z:3}))  #代入y=2,z=3
print("y=2,z=3时，expr2=",expr2.subs({y:2,z:3}).n())  #以浮点数显示计算结果

together和apart方法使用示例如下：

from sympy import *
x1,x2,x3,x4=symbols('m1:5'); x=symbols('x')
print(x1/x2+x3/x4)
print(together(x1/x2+x3/x4))#展开
print((2*x**2+3*x+4)/(x+1))
print(simplify((2*x**2+3*x+4)/(x+1)))  #化简没有效果
print(apart((2*x**2+3*x+4)/(x+1)))

 1.2 用SymPy做符号函数画图

from sympy.plotting import plot
from sympy.abc import x , pi
from sympy.functions import sin,cos

plot((2*sin(x),(x,-6,6)),(cos(x + pi/4),(x,-5,5)))

 

from sympy.plotting import plot3d
from sympy.abc import x , pi
from sympy.functions import sin,sqrt

plot3d(sin(sqrt(x**2 + y**2)),(x,-10,10),(y,-10,10),xlabel = '$x$',ylabel = '$y$')

 

from sympy import plot_implicit as pt,Eq
from sympy.abc import x,y
pt(Eq((x-1)**2 + (y-2)**3,4),(x,-6,6),(y,-4,4),xlabel = '$x$',ylabel = '$y$')

2. 高等数学的符号解

2.1 极限

求极限用limit()

from sympy import *
x = symbols('x')
print(limit(sin(x)/x,x,0))#求出1
print(limit((1 + 1/x)**x,x,oo))#求出e

2.2 导数 

 

 求导数用diff()

from sympy import *
x,y = symbols('x y')
z = sin(x) + x**2 * exp(y)
#二阶偏导数
print(diff(z,x,2))#求出2*exp(y) - sin(x)
#一阶偏导数
print(diff(z,y))#求出x**2*exp(y)

2.3 级数求和 

factor可以把计算结果因式分解，级数求和用summation

from sympy import*
k,n=symbols ('k n')
print(summation(k**2, (k, 1,n)))#n**3/3 + n**2/2 + n/6
print(factor(summation(k**2, (k, 1,n))))#n*(n + 1)*(2*n + 1)/6
print(summation(1/k**2,(k,1,oo)))#pi**2/6

2.4 泰勒展开 

 

"""级数展开：series(函数表达式, x0, n）,使用.removeO()去除皮亚诺余项，remove后面的o大写"""
from sympy import*
from sympy.plotting import*
x=symbols('x'); 
y=sin(x)
for k in range(3,8,2): 
    print(y.series(x,0,k))
plot(y,series(y, x, 0, 3).removeO(),series(y, x, 0, 5).removeO(),series(y, x, 0, 7).removeO(),(x,0,2),xlabel = '$x$',ylabel = '$y$')

2.5 不定积分和定积分 

不定积分用integrate 

from sympy import integrate,symbols,pi,oo,sin
x=symbols ('x')
print(integrate(sin(2*x),(x,0,pi)))#0
print(integrate(sin(x)/x,(x,0,oo)))#pi/2

2.6 代数方程 

 

求方程使用solve

from sympy import*
x,y=symbols('x y')
print(solve(x**3-1,x))
print(solve((x-2)**2*(x-1)**3,x))
print(roots((x-2)**2*(x-1)**3,x))#roots得到根重数的情况

 

from sympy import*
x,y=symbols('x y')
print(solve([x**2 + y**2 -1,x - y],[x,y]))#[(-sqrt(2)/2, -sqrt(2)/2), (sqrt(2)/2, sqrt(2)/2)]

from sympy import *
x=symbols('x'); y=2*x**3-5*x**2+x
x0=solve(diff(y,x),x)   #求驻点
print("驻点的精确解为",x0)
print("驻点的浮点数表示为：",[x0[i].n() for i in range(len(x0))])  #列表中的符号数无法整体转换为浮点数
y0=[y.subs(x,0),y.subs(x,1),y.subs(x,x0[0]).n()] #代入区间端点和一个驻点的值
print("三个点的函数值分别为:",y0)

2.7 微分方程 

sympy库提供desolve求常微分方程的符号解，在声明时可以使用Function()函数。

from sympy import *
x=symbols('x'); 
y=symbols('y',cls=Function)#y = Function('y')
eq1=diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)
eq2=diff(y(x),x,2)-5*diff(y(x),x)+6*y(x)-x*exp(2*x)
print("齐次方程的解为：",dsolve(eq1,y(x)))
print("非齐次方程的解为：",dsolve(eq2,y(x)))

from sympy import *
x = symbols('x')
y = Function('y')
eq1 = diff(y(x),x,2) - 5*diff(y(x),x) + 6*y(x)
eq2 = diff(y(x),x,x) - 5*diff(y(x),x) + 6*y(x) - x*exp(2*x)
print(dsolve(eq1,y(x),ics={y(0):1,diff(y(x),x).subs(x,0):0}))
print(dsolve(eq2,y(x),ics={y(0):1,y(2):0}))

3. 高等数学问题的数值解

大多数实际问题无法用符号解，只能求数值解，即近似值。

3.1 一重积分

一重积分可以用梯形公式、辛普森公式或者sympy库的quad直接求解

3.1.1 梯形计算

def trapezoid(f,n,a,b):    #定义梯形公式的函数
    xi=np.linspace(a,b,n); h=(b-a)/(n-1)
    return h*(np.sum(f(xi))-(f(a)+f(b))/2)

3.1.2 辛普森计算

def simpson(f,n,a,b):     #定义辛普森公式的函数
    xi, h=np.linspace(a,b,2*n+1), (b-a)/(2.0*n)
    xe=[f(xi[i]) for i in range(len(xi)) if i%2==0]
    xo=[f(xi[i]) for i in range(len(xi)) if i%2!=0]
    return h*(2*np.sum(xe)+4*np.sum(xo)-f(a)-f(b))/3.0

 3.2 多重积分

多重积分使用dblquad和tplquad直接求解数值解。

import numpy as np
from scipy.integrate import dblquad

f1=lambda y, x: x*y**2  #第一个被积函数
print("I1：",dblquad(f1, 0, 2, 0, 1))

f2=lambda y, x: np.exp(-x**2/2)*np.sin(x**2+y)
bd=lambda x: np.sqrt(1-x**2)
print("I2:",dblquad(f2, -1, 1, lambda x: -bd(x), bd))

import numpy as np
from scipy.integrate import tplquad
f=lambda z, y, x: z*np.sqrt(x**2+y**2+1)
ybd=lambda x: np.sqrt(2*x-x**2)
print("I=",tplquad(f, 0, 2, lambda x: -ybd(x),ybd, 0, 6))

 【注】必须按照积分次序来书写匿名函数的自变量顺序

3.3 非线性方程数值解

3.3.1 二分法求根

def binary_search(f, eps, a, b):  #二分法函数
    c=(a+b)/2
    while np.abs(f(c))>eps:
        if f(a)*f(c)<0: b=c
        else: a=c
        c=(a+b)/2
    return c

3.3.2 牛顿迭代法求根

def newton_iter(f, eps, x0, dx=1E-8):  #牛顿迭代法函数
    def diff(f, dx=dx):   #求数值导数函数
        return lambda x: (f(x+dx)-f(x-dx))/(2*dx)
    df=diff(f,dx)
    x1=x0-f(x0)/df(x0)
    while np.abs(x1-x0)>=eps:
        x1, x0=x1-f(x1)/df(x1), x1
    return x1

3.3.3 scipy工具库求解

import numpy as np
from scipy.optimize import fsolve

def binary_search(f, eps, a, b):  #二分法函数
    c=(a+b)/2
    while np.abs(f(c))>eps:
        if f(a)*f(c)<0: b=c
        else: a=c
        c=(a+b)/2
    return c

def newton_iter(f, eps, x0, dx=1E-8):  #牛顿迭代法函数
    def diff(f, dx=dx):   #求数值导数函数
        return lambda x: (f(x+dx)-f(x-dx))/(2*dx)
    df=diff(f,dx)
    x1=x0-f(x0)/df(x0)
    while np.abs(x1-x0)>=eps:
        x1, x0=x1-f(x1)/df(x1), x1
    return x1

f=lambda x: x**3+1.1*x**2+0.9*x-1.4
print("二分法求得的根为：", binary_search(f,1E-6,0,1))
print("牛顿迭代法求得的根为：",newton_iter(f,1E-6,0))
print("直接调用SciPy求得的根为：",fsolve(f,0))

 

from numpy import sin
from scipy.optimize import fsolve
f=lambda x: [5*x[1]+3, 4*x[0]**2-2*sin(x[1]*x[2]), x[1]*x[2]-1.5]
print("result=",fsolve(f, [1.0, 1.0, 1.0]))


#方法二
from numpy import sin
from scipy.optimize import fsolve
def Pfun(x):
    x1,x2,x3=x.tolist()  #x转换成列表
    return 5*x2+3, 4*x1**2-2*sin(x2*x3), x2*x3-1.5
print("result=",fsolve(Pfun, [1.0, 1.0, 1.0]))

 3.4 极值点的数值解

3.4.1 一元函数

（1）在区间上求解极小点用fminbound

from numpy import exp,cos
from scipy.optimize import fminbound
f=lambda x: exp(x)*cos(2*x)
x0=fminbound(f,0,3)
print("极小点为：{}，极小值为：{}".format(x0,f(x0)))

（2）求在某个点附近的极小值点用fmin

from numpy import exp,cos
from scipy.optimize import fmin
f=lambda x: exp(x)*cos(2*x)
x0=fmin(f,0)
print("极小点为：{}，极小值为：{}".format(x0,f(x0)))

3.4.2 多元函数

多元函数求解极小值点用minimize

from scipy.optimize import minimize
f=lambda x: 100*(x[1]-x[0]**2)**2+(1-x[0])**2; 
x0=minimize(f,[2.0, 2.0])
print("极小点为：{}，极小值为：{}".format(x0.x,x0.fun))

4. 线性代数的符号解和数值解

 4.1 线性方程组

import sympy as sp
A = sp.Matrix([[2,1,-5,1],[1,-3,0,-6],[0,2,-1,2],[1,4,-7,6]])
B = sp.Matrix([8,6,-2,2])
B.transpose()
print(A.rank())#秩
print(A.inv()*B)#惟一解

4.2 齐次线性方程组 nullspace

import sympy as sp
A=sp.Matrix([[1, -5, 2, -3], [5, 3, 6, -1], [2, 4, 2, 1]])
print(A.nullspace())#基础解系

4.3 非齐次线性方程

import sympy as sp
A=sp.Matrix([[1, 1, -3, -1],[3, -1, -3, 4], [1, 5, -9, -8]])
b=sp.Matrix([1, 4, 0]); 
b.transpose()
C=A.row_join(b)  #构造增广矩阵
print("增广阵的行最简形为：\n",C.rref())

4.4 特征值与特征向量

 eigenvals ()求特征值，eigenvects ()求特征向量

4.5 可逆矩阵与对角阵

使用diagonalize()求解，is_diagonalizable ()用来判断矩阵是否可以对角化