算法练习-分割等和子集（思路+流程图+代码）

难度参考

        难度：困难

        分类：动态规划

        难度与分类由我所参与的培训课程提供，但需 要注意的是，难度与分类仅供参考。且所在课程未提供测试平台，故实现代码主要为自行测试的那种，以下内容均为个人笔记，旨在督促自己认真学习。

题目

        给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。注意：每个数组中的元素不会超过100数组的大小不会超过200

        示例1:输入：[1，5，11，5]

        输出：true

        解释：数组可以分割成[1，5，5]和[11]。

        示例2:

        输入：[1，2，3，5]

        输出：false

        解释：数组不能分割成两个元素和相等的子集。

        提示：1 <= nums.length <= 2008 1 <= nums[i] <= 100

思路

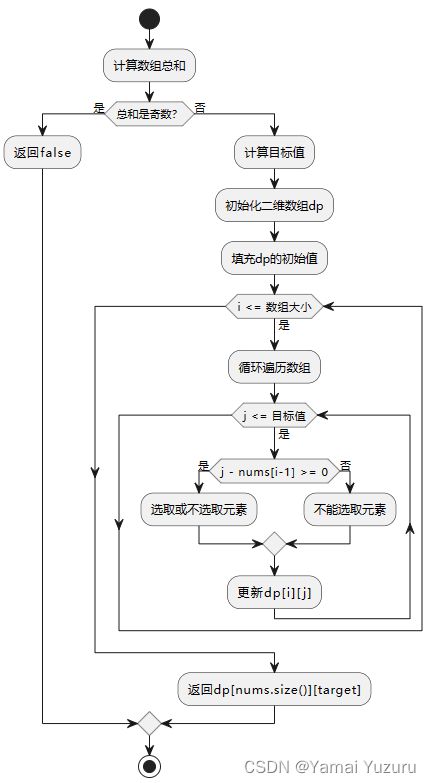
        1. 计算总和并判断：

        首先计算给定数组的所有元素之和。如果总和是奇数，那么不可能将数组分割成两个和相等的子集，因为两个相等的数加起来一定是偶数。如果总和是偶数，那么我们的目标是找到一个子集，其和为总和的一半。

        2. 动态规划数组的定义：

        定义一个二维数组`dp`，其中`dp[i][j]`表示从数组的前i个元素中选取一些，是否能够使它们的和等于j。由此，我们的目标转换为判断`dp[n][sum/2]`是否为真，其中n是数组的长度。

        3. 初始化：

        dp[i][0]为真，因为不选取任何元素时，任何前i个元素的和都可以为0。dp[0][j]（除了`dp[0][0]`）为假，因为没有元素可以组成非零的j。

        4. 状态转移方：

        对于每个元素`nums[i]`和每个目标和j，我们有两种选择：不选取nums[i]，这时dp[i][j] = dp[i-1][j]；选取nums[i]，这时dp[i][j] = dp[i-1][j-nums[i]]。因此，dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]。

        5. 结果：

        查看dp[n][sum/2]的值，如果为真，说明可以分割成两个和相等的子集。

示例

        假设nums = [1, 5, 11, 5]，我们需要填充到dp[4][11]。

        初始化

        - sum = 22
        - target = sum / 2 = 11
        - 初始化dp表，dp[i][0] = true，其他为false。

        Step 1: i = 1, nums[i-1] = 1

        更新dp[1][j]，其中j = 1时，dp[1][1] = true。

dp = [
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, false, false, false, false, false, false, false],
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, false, false, false, false, false, false, false, false, false, false, false]
]

        Step 2: i = 2, nums[i-1] = 5

        我们可以更新dp[2][1], dp[2][5]为true。

dp = [
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, true,  false, false, false, false, false, false],
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, false, false, false, false, false, false, false, false, false, false, false]
]

        Step 3: i = 3, nums[i-1] = 11

        更新dp[3][1], dp[3][5], dp[3][11]为true。由于11正好是nums[i-1]，所以dp[3][11] = true。

dp = [
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, true,  false, false, false, false, false, false],
[true, true,  false, false, false, true,  false, false, false, false, true, false],
[true, false, false, false, false, false, false, false, false, false, false, false]
]

        Step 4: i = 4, nums[i-1] = 5

        最后一行考虑所有数字。我们更新dp[4][j]。由于nums[3] = 5，我们可以更新dp[4][6], dp[4][10], dp[4][11]等。

        最终状态（部分更新示例）：

dp = [
[true, false, false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, false, false, false, false, false, false, false],
[true, true,  false, false, false, true,  false, false, false, false, false, false],
[true, true,  false, false, false, true,  false, false, false, false, true, false],
[true, true,  false, false, false, true,  true,  false, false, false, true, true]
]

        注意：由于空间限制，上面的dp表没有展示所有中间步骤的更新。在实际操作中，你会发现dp[i][j]的更新依赖于前一行的结果，以及当前行之前的结果（如果j >= nums[i-1]）。

        结果

        最终，我们关注的是dp[4][11]的值，它是true。这意味着可以将数组[1, 5, 11, 5]分割成两个和为11的子集，例如[1, 5, 5]和[11]。因此，canPartition函数返回true。

梳理

                实际上，"分割等和子集"问题不是一个经典的0-1背包问题的变种。

        针对"分割等和子集"问题，我们可以使用以下递推公式来求解：

        假设给定的数组为nums，数组的元素和为sum。我们想在数组中找到一个子集，使得这个子集的和等于sum / 2。那么，我们需要考虑以下两种情况：

1. 不选择当前元素nums[i]，即dp[i][j] = dp[i-1][j]。
2. 选择当前元素nums[i]，即dp[i][j] = dp[i-1][j-nums[i]]。

        其中，dp[i][j]表示从数组nums的[0, i-1]下标范围内选取若干个元素，使得它们的和等于j。那么，我们可以得到递推公式：

dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]]

        其中，dp[i][j]表示从前i个元素中，是否存在一个子集的和等于j。如果dp[i-1][j]为true，则表示前i-1个元素中存在一个子集的和等于j，那么不选择当前元素nums[i]也可以满足条件，所以dp[i][j]为true。如果dp[i-1][j-nums[i]]为true，则表示前i-1个元素中存在一个子集的和等于j-nums[i]，那么选择当前元素nums[i]后，该子集加上nums[i]的和等于j，也可以满足条件，所以dp[i][j]为true。

        这样，我们可以使用动态规划的方式从前往后填充dp表格，直到填充完整个表格。最终，dp[n][sum/2]的值表示是否存在一个子集的和等于原数组和的一半，如果为true，则表示可以分割成两个和相等的子集；如果为false，则表示无法分割成两个和相等的子集。

代码

#include 
#include  // 用于计算数组和
using namespace std;

bool canPartition(vector& nums) {
    int sum = accumulate(nums.begin(), nums.end(), 0); // 计算数组总和
    if (sum % 2 != 0) return false; // 如果总和是奇数，则不能分割成两个和相等的子集
    int target = sum / 2;
    vector> dp(nums.size() + 1, vector(target + 1, false));
    // 初始化
    for (int i = 0; i <= nums.size(); ++i) {
        dp[i][0] = true;
    }
    // 动态规划填表
    for (int i = 1; i <= nums.size(); ++i) {
        for (int j = 1; j <= target; ++j) {
            if (j - nums[i-1] >= 0) {
                // 选取这个元素或不选取这个元素
                dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
            } else {
                // 不能选取这个元素
                dp[i][j] = dp[i-1][j];
            }
        }
    }
    return dp[nums.size()][target];
}

• 时间复杂度： O(n * sum)。

• 空间复杂度： O(nums.size() * target)。

打卡