【吴恩达·机器学习】第二章：多变量线性回归模型（选择学习率、特征缩放、特征工程、多项式回归）

• 博主简介：努力学习的22级计算机科学与技术本科生一枚
• 博主主页： @Yaoyao2024
• 每日一言: 勇敢的人，不是不落泪的人，而是愿意含着泪继续奔跑的人。
  ——《朗读者》
  

0、声明

本系列博客文章是博主本人根据吴恩达老师2022年的机器学习课程所学而写，主要包括老师的核心讲义和自己的理解。在上完课后对课程内容进行回顾和整合，从而加深自己对知识的理解，也方便自己以及后续的同学们复习和回顾。

• 课程地址2022吴恩达机器学习Deeplearning.ai课程
• 课程资料和代码（jupyter notebook)2022-Machine-Learning-Specialization

由于课程使用英文授课，所以博客中的表达也会用到英文，会用到中文辅助理解。

Machine learning specialization课程共分为三部分

• 第一部分：Supervised Machine Learning: Regression and Classification
• 第二部分：Advanced Learning Algorithms（Neural networks、Decision Trees)
• 第三部分：Unsupervised Learning: Recommenders, Reinforcement Learning

最后，感谢吴恩达老师Andrew Ng的无私奉献，和视频搬运同学以及课程资料整合同学的无私付出。Cheers!

前言

 在前一章中我们学习了单变量线性回归算法.多变量线性回归的整体思想和单变量的是一致的。主要不同在于 输入变量（也成为“特征;feature)是多个，于是会引入 向量化;vectorization将输入变量进行向量化，加快运行速度和简化书写。这一章中当然也是有梯度下降算法来进行模型训练，主要思想已经在前一章中详细讲到，这里只是看看多变量的梯度下降实现与单变量的不同之处、如何判断梯度下降正确运行。关于学习率，前一章中主要介绍了学习率，以及学习率的大小设置不同从而对梯度下降的影响；这一章将详细讲解一下如何设置学习率，从而能更好地运行梯度下降。此外，由于多变量线性回归模型的"multiple features"的特点，会给出一些基于这个模型的一些建议：特征缩放、特征工程、多项式回归。

‍♀️接下来让我们开始吧！

1、多变量线性回归

如下图所示，多变量线性回归问题的主要不同点就在于：多特征（多个输入变量）。

且我们将多个输入变量x向量化为一个向量x，简化书写（还有加快运行速度，我们下面介绍）

把输入变量进行向量化之后。回归模型和单变量回归模型几乎一样。

1.1：向量化（vectorization）

• 向量的定义.
  在这门课中的向量，都是在数组中有序排列的数字。数组中元素的数量通常称为维度.一个向量中的单个元素会有下标，在编程中(如我们经常使用的Numpy）下标是0~n-1；在数学和本门课中，下标是1~n，
  

• 向量化的好处

  • ✅make your code shorter
  • ✅make it run much more efficiently

• 对比：从下图可以看出，使用向量化后的代码比没有使用向量化的代码更简洁。其实背后的运行效率也更高。
  

• 向量化的实现
  可以看到，对于连加操作。向量化使用numpy进行向量点乘的方法，是通过把向量从一块连续的存储空间取出， 并行运算点乘结果，再相加。而不是把元素从连续的空间取出一个相加，再取出一个。
  
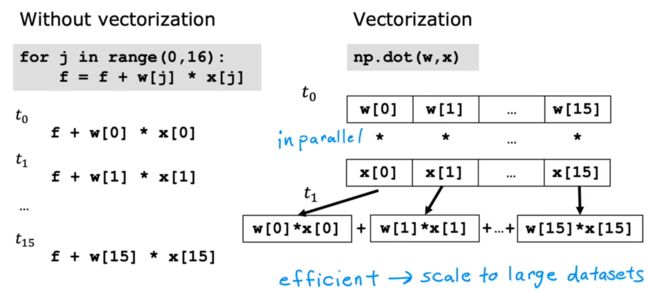
  也如下图所示，向量化提升计算效率的地方就是在各个向量计算过程中。下图举例在梯度下降过程中进行向量的并行计算，效率比循环高得多
  

1.2：梯度下降（判断是否收敛）

• 对比单变量.

判断梯度下降是否正确进行有如下图两种方式

• ✅ 学习曲线（learning curve)
  当梯度下降正确进行时，随着横轴迭代次数（参数更新次数）的增加，代价函数此时的值会逐渐下降；并且达到一定迭代次数后，代价函数值将趋于平缓。
• ✅ 自动收敛测试（automatic convergence test)
  设置一个ε，当代价函数下降小于ε时，就可以认为达到收敛。

一般还是倾向于用学习曲线进行判断，因为找到一个合适的ε比较困难。

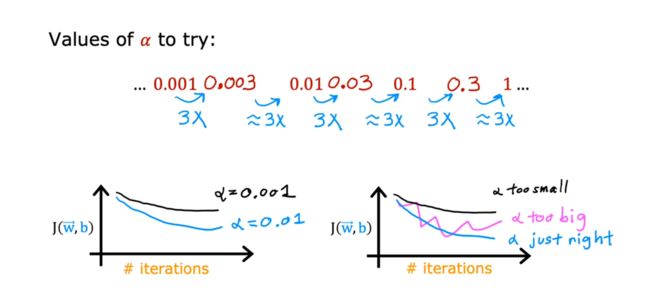
1.3：学习率的设置

首先需要明白： 最终得目标是让学习曲线快速收敛

也没有什么固定的技巧。就是从小的开始尝试，一边增加学习率，一边观察学习曲线。知道学习曲线能达到理想的状态。

2、实用技巧

2.1：特征缩放(feature scaling)

我们先从下面一个例子入手，分析为什么需要进行特征缩放。

下图可以看到，x1和x2不是一个数量级,在进行梯度下降算法时，在w和b不确定时，计算代价函数很容易会远超于合理值。

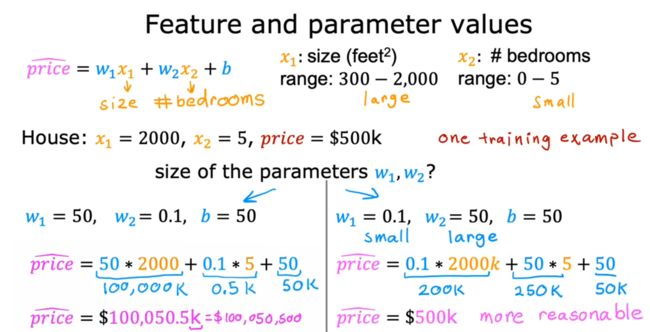
此时梯度下降过程如下图所示：

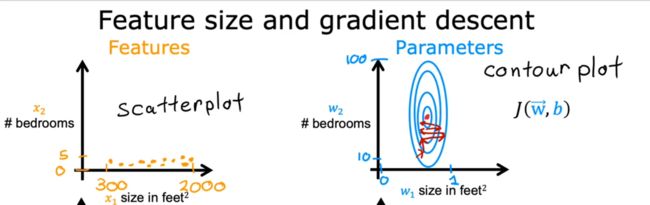
可以看到，梯度下降过程十分缓慢。

解决这一问题的关键就是：特征缩放。即：将特征的数量级都缩放到一个数量级上，这样可以使得梯度下降更高效的运行。

feature scaling: rescale the different features, so they all take on comparable range of values, values can speed up gradient descent significantly.

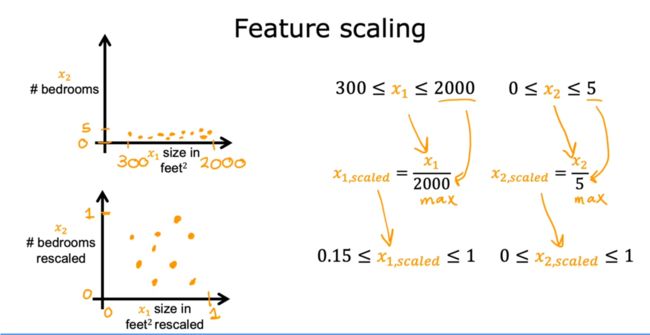
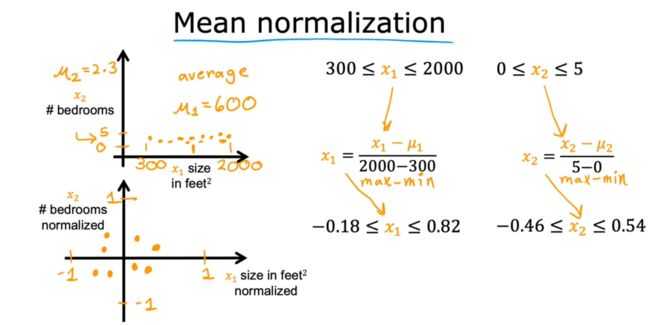
具体进行特征缩放的实现方法有以下几种

• 除最大值
  

• Mean normalization
  

• Z-score normalization
  

✅总结：特征应在一个数量级（如不在，则进行特征缩放），这样可以时梯度下降运行得更快！

2.2：特征工程（feature engineering)

即：利用现有特征设计新的特征。

对于机器学习来说，需要自己设计特征，所以选择和输入良好的特征是使算法良好运行的关键步骤。

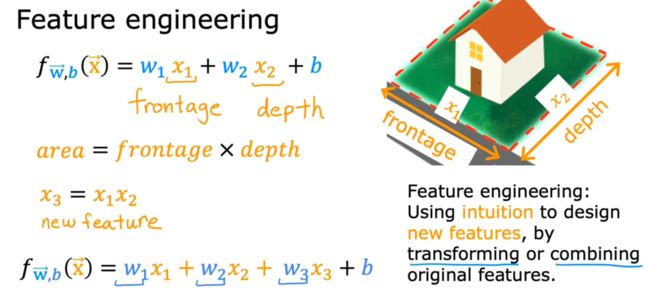
2.3：多项式回归

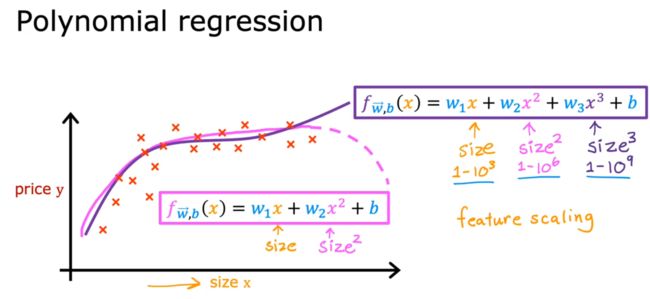
使用了特征工程，我们不仅可以拟合线性的函数，还可以拟合非线性，从而使模型更好的运行。

所以可以认为：线性模型+特征工程 = 多项式回归。

Tips:在运用多项式回归时，注意特征缩放

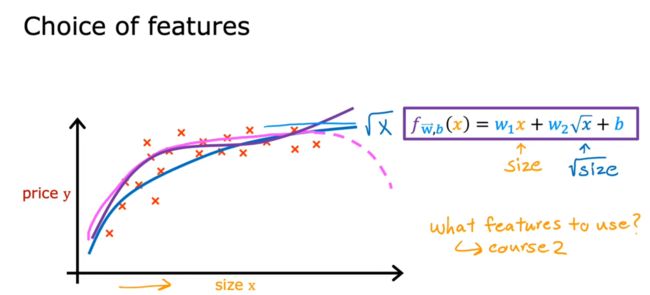
从下图可以看到，特征的选择不只有一种。通过后面章节中学习对模型进行评价的方法，我们可以知道如何选择合适的特征。

---

下期预告：逻辑回归模型、正则化