【算法 - 二叉树】“一套逻辑”搞定二叉树 - 2！

上一篇文章我们通过几道有关二叉树类型判断的题目，体会到了“二叉树递归”的套路。我们再来回顾一下（还没看过上篇文章的赶快 点我 查看哦！）

1. 分析当前结点需要哪些二叉树的信息才能完成条件判断，整合成一个 结构体;

2. 分别 递归调用 左右子树寻找该信息；

3. 得到左右子树的信息后，思考怎样对该 信息加工 判断。

本篇文章我们继续 使用套路 解决二叉树的一些题目！

完全二叉树

判断一棵二叉树是否为 完全二叉树。

public static class Info {
    public boolean isFull;
    public boolean isCBT;
    public int height;

    public Info(boolean full, boolean cbt, int h) {
        isFull = full;
        isCBT = cbt;
        height = h;
    }
}

public static boolean isCBT(Node head) {
    if (head == null) {
        return true;
    }
    return process(head).isCBT;
}


public static Info process(Node h) {
    if (h == null) {
        return new Info(true, true, 0);
    }
    Info leftInfo = process(h.left);
    Info rightInfo = process(h.right);

    int height = Math.max(leftInfo.height, rightInfo.height) + 1;
    boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
    boolean isCBT = false;

    if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
        isCBT = true;
    } else if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
        isCBT = true;
    } else if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
        isCBT = true;
    } else if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) {
        isCBT = true;
    }
    return new Info(isFull, isCBT, height);
}

思路

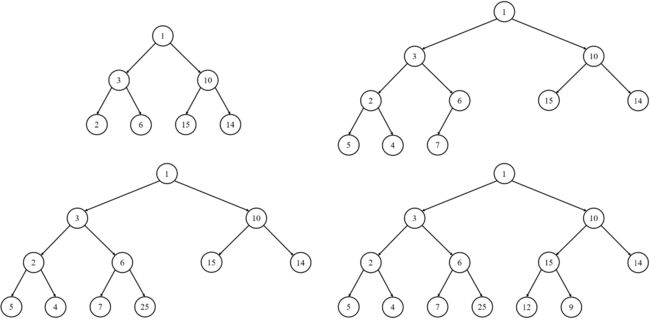
若一棵树为完全二叉树，则可能出现的情况有：

1. 左右子树均为满二叉树，且左子树高度 == 右子树高度

2. 左子树是完全二叉树，右子树是满二叉树，且左子树高度 = 右子树高度 + 1

3. 左右子树均为满二叉树，且左子树高度 = 右子树高度 + 1

4. 左子树是满二叉树，右子树是完全二叉树，左树高度 == 右树高度

因此，需要的信息就包括三个：

1.是否是满二叉树

2.是否是完全二叉树

3.树高

代码解释

首先定义结构体，包含布尔类型的 isFull 、布尔类型的 isCBT 和整型 height 三个信息。

Info process(Node h) 函数进行主要判断：

• base case 是 h 为空时，返回 (true,true,0) 。空树既是 完全二叉树，也是 满二叉树 且高度为 0 ；

分别递归调用左右子树并记录信息。

• height 高度信息设置为左右子树的 最大值 + 当前结点的 1 高度。
• 满二叉树 要求严格，必须左右子树均为满二叉树且高度相同。
• 在判断是否为 完全二叉树 时，只需根据思路分析中的四种情况一一列举即可。

最终返回isFull、isCBT 和 height三个信息。主函数传入根结点，返回根结点的isCBT值即可：process(head).isCBT。

力扣194. 最近公共祖先

对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）

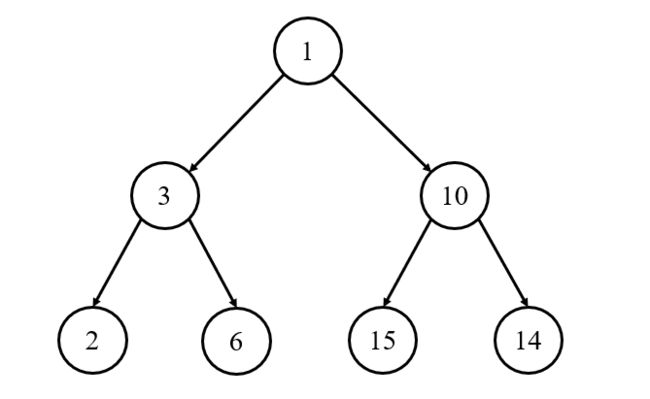
例如：3 和 15 的最低公共祖先为 1。

public static class Info {
    public boolean findA;
    public boolean findB;
    public Node ans;

    public Info(boolean fA, boolean fB, Node an) {
        findA = fA;
        findB = fB;
        ans = an;
    }
}

public static Node lowestAncestor(Node head, Node a, Node b) {
    return process(head, a, b).ans;
}

public static Info process(Node h, Node a, Node b) {
    if (h == null) {
        return new Info(false, false, null);
    }
    Info leftInfo = process(h.left, a, b);
    Info rightInfo = process(h.right, a, b);

    boolean findA = (h == a) || leftInfo.findA || rightInfo.findA;
    boolean findB = (h == b) || leftInfo.findB || rightInfo.findB;

    Node ans = null;
    if (leftInfo.ans != null) {            // 左树已经出现答案了
        ans = leftInfo.ans;
    } else if (rightInfo.ans != null) {    // 右树已经出现答案了
        ans = rightInfo.ans;
    } else {
        if (findA && findB) {
            ans = h;
        }
    }
    return new Info(findA, findB, ans);
}

思路

对于任意一个结点h来说，左右两个子树中是否存在要寻找的结点 A，B。可以分为两种情况考虑：

与结点 h 有关时（h为最近公共祖先）

1. 左右子树中分别找到了一个（一个在左，一个在右）；

2. h == a, 左 或 右子树中找到了 b

3. h == b, 左 或 右子树中找到了 a

与结点 h 无关时（h不是最近公共祖先）

1. 左右子树中并没有分别找到 a 和 b；

2. a 和 b 在 h 的 左子树 中已经 汇合 了；

3. a 和 b 在 h 的 右子树 中已经 汇合 了；

因此，需要的信息就包括三个：

1.是否找到了 a

2.是否找到了 b

3.汇合的结点

代码解释

首先定义结构体，包含布尔类型的findA、findB和Node类型的ans三个信息。

Info process(Node h) 函数进行主要判断：

• base case 是 h 为空时，返回 (false,false,null) 。表示没有找到A、B，也没有公共祖先；

分别递归调用左右子树并记录信息。

• 只要其中一个子树找到了 A 或者 该结点就是 A ，即找到了 A（B也同理）。
• 1）如果左或右子树出现了公共结点，那答案就是该公共结点；
• 2）如果左右子树都没出现公共结点，并且左右子树都分别找到了A，B，说明该结点就是AB最近的公共结点。

最终返回findA、findB 和 ans三个信息。主函数传入根结点，返回根结点的ans值即可：process(head).ans。

---

相信通过上篇文章和本文的学习，小伙伴们对于 二叉树的递归套路 已经非常熟悉了。可以通过下面这道力扣题目再练习一下哦！

543.二叉树的直径

给你一棵二叉树的根节点，返回该树的直径。

二叉树的 直径 是指树中 任意两个节点 之间 最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

---

二叉树递归套路大总结

1. 分析当前结点需要哪些 左右子树 的信息才能完成条件判断，整合成一个 结构体;

2. 分别 递归调用 左右子树寻找该信息；

3. 得到左右子树的信息后，思考怎样对该 信息加工 判断。

代码模板：

public static class Info {
    public boolean ？;
    public Node ？;
    public int ？;

    public Info(boolean ？, Node ？, int ?) {
        ？ = ？;
        ？ = ？;
        ？ = ？;
    }
}

public static Node f(Node head, ...) {
    return process(head, ...).？;
}

public static Info process(Node h,...) {
    if (h == null) {
        return new Info(...);
    }
    Info leftInfo = process(h,...);
    Info rightInfo = process(h,...);

    boolean ？ = ...;
    Node ？ = ...;
    int ？= ...;
    
    return new Info(..., ..., ...);
}

有了这套模板，二叉树有关的 dp 问题思考起来是不是就非常容易啦！

你学会了么？

~ 点赞 ~ 关注 ~ 不迷路 ~！！！