【数据结构题目讲解】洛谷P4219 大融合

P4219 大融合

$\mathrm{Description}$

给定 $1$ 棵 $n$ 个节点的树，树的边是在操作中加入的，接下来有 $m$ 次操作：

• 将 $x$ 与 $y$ 之间连一条边
• 查询 $x$ 与 $y$ 之间这条边有多少条经过该边的简单路径

$\mathrm{Solution}$

对于加边的操作，是很难在线操作的，所以可以考虑离线下，现将这棵树建出来。

对于有多少条经过 $(x,y)$ 的简单路径就等同于若 $y$ 为 $x$ 的父节点，则为 $S{z}_x\times (S{z}_{roo{t}_y}-S{z}_y)$。其中 $S{z}_i$ 表示 $i$ 子树的大小，$roo{t}_i$ 表示当前 $i$ 的根节点。

所以，问题转化为了如何快速求解 $Sz$ 以及 $root$。

对于 $Sz$，观察当 $1$ 条边加入之后，哪些点会发生变化，

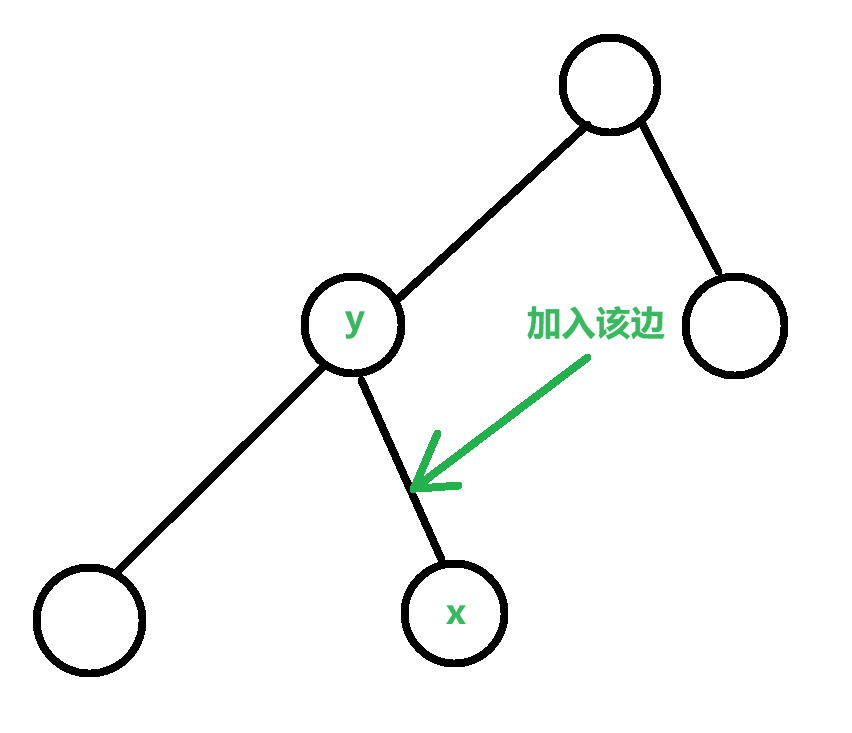
比如说，加入边 $(x,y)$，令 $y$ 为 $x$ 的父节点。则当加入 $y$ 之后变化的应该是哪些点呢？

首先，$y$ 节点的 $Sz$ 肯定要加上 $S{z}_x$，还有别的点吗？$y$ 到 $roo{t}_y$ 其实都应该加上 $S{z}_x$

这样就可以维护出 $Sz$

那么，$root$ 怎么维护呢？这个直接用并查集即可，并查集的根节点就是当前所在树的根节点。对于加入边 $(x,y)$，则令 $roo{t}_{\text{find}(x)}=\text{find}(y)$，其中 $y$ 为 $x$ 的父节点。

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 1e5 + 10;

int N, Q;
struct Node
{
	char Op;
	int x, y;
};
std::vector<Node> Qry;
std::vector<int> G[SIZE], DFS_Order;
int Depth[SIZE], Fa[SIZE][32], Vis[SIZE], P[SIZE], Sz[SIZE], Pos[SIZE];

int Find(int x)
{
	if (x != P[x]) P[x] = Find(P[x]);
	return P[x];
}

void DFS(int u, int fa)
{
	DFS_Order.push_back(u), Pos[u] = DFS_Order.size() - 1;
	Sz[u] = 1;
	for (auto v : G[u])
	{
		if (v == fa) continue;
		DFS(v, u);
		Sz[u] += Sz[v];
	}
}

void BFS(int root)
{
    memset(Depth, 0x3f, sizeof Depth);
    queue<int> q;
    q.push(root);
    Depth[0] = 0, Depth[root] = 1;

    while (q.size())
    {
        int t = q.front();
        q.pop();

        if (Vis[t]) continue;
        Vis[t] = 1;

        for (auto j : G[t])
            if (Depth[j] > Depth[t] + 1)
            {
                Depth[j] = Depth[t] + 1;
                q.push(j);
                Fa[j][0] = t;
                for (int k = 1; k <= 22; k ++)
                    Fa[j][k] = Fa[Fa[j][k - 1]][k - 1];
            }
    }
}

int LCA(int a, int b)
{
	if (Depth[a] < Depth[b]) swap(a, b);
    for (int k = 22; k >= 0; k --)
        if (Depth[Fa[a][k]] >= Depth[b])
            a = Fa[a][k];

    if (a == b) return a;

    for (int k = 22; k >= 0; k --)
        if (Fa[a][k] != Fa[b][k])
            a = Fa[a][k], b = Fa[b][k];

    return Fa[a][0];
}

struct Segment
{
	int l, r;
	int Sum;
}Tree[SIZE << 2];

void Pushup(int u) { Tree[u].Sum = Tree[u << 1].Sum + Tree[u << 1 | 1].Sum; }

void Build(int u, int l, int r)
{
	if (l == r)
	{
		Tree[u] = {l, r};
		return;
	}

	Tree[u] = {l, r};
	int mid = l + r >> 1;
	Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
	Pushup(u);
}

void Modify(int u, int x, int d)
{
	if (Tree[u].l == Tree[u].r)
	{
		Tree[u].Sum += d;
		return;
	}

	int mid = Tree[u].l + Tree[u].r >> 1;
	if (mid >= x) Modify(u << 1, x, d);
	else Modify(u << 1 | 1, x, d);
	Pushup(u);
}

int Query(int u, int l, int r)
{
	if (Tree[u].l >= l && Tree[u].r <= r)
		return Tree[u].Sum;

	int mid = Tree[u].l + Tree[u].r >> 1, Result = 0;
	if (mid >= l) Result += Query(u << 1, l, r);
	if (mid < r) Result += Query(u << 1 | 1, l, r);
	return Result;
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> Q;

	for (int i = 1; i <= N; i ++)
		P[i] = i;

	char Op;
	int x, y;
	for (int i = 1; i <= Q; i ++)
	{
		cin >> Op >> x >> y, Qry.push_back({Op, x, y});
		if (Op == 'A') G[x].push_back(y), G[y].push_back(x);
	}

	DFS_Order.push_back(0);
	for (int i = 1; i <= N; i ++)
		if (!Vis[i])
			BFS(i), DFS(i, -1);

	Build(1, 1, N);

	for (int i = 1; i <= N; i ++)
	{
		Modify(1, Pos[i], 1);
		if (Pos[Fa[i][0]] != 0) Modify(1, Pos[Fa[i][0]], -1);
	}

	for (auto v : Qry)
	{
		int x = v.x, y = v.y;
		if (Fa[x][0] != y) swap(x, y);
		if (v.Op == 'A')
		{
			int V = Query(1, Pos[x], Pos[x] + Sz[x] - 1);
			Modify(1, Pos[y], V);
			if (Fa[Find(y)][0] != 0) Modify(1, Pos[Fa[Find(y)][0]], -V);
			P[Find(x)] = Find(y);
		}
		else
		{
			int Vy = Query(1, Pos[Find(y)], Pos[Find(y)] + Sz[Find(y)] - 1) - Query(1, Pos[x], Pos[x] + Sz[x] - 1);
			int Vx = Query(1, Pos[x], Pos[x] + Sz[x] - 1);
			cout << Vy * Vx << endl;
		}
	}

	return 0;
}