MC, MCMC, Gibbs採样 原理&实现(in R)
本文用讲一下指定分布的随机抽样方法:MC(Monte Carlo), MC(Markov Chain), MCMC(Markov Chain Monte Carlo)的基本原理,并用R语言实现了几个样例:
1. Markov Chain (马尔科夫链)
2. Random Walk(随机游走)
3. MCMC详细方法:
3.1 M-H法
3.2 Gibbs採样
PS:本篇blog为ese机器学习短期班參考资料(20140516课程),课上讲详述。
以下三节分别就前面几点简要介绍基本概念,并附上代码。这里的概念我会用最最naive的话去概括,详细内容就看我最下方推荐的链接吧(*^__^*)
0. MC(Monte Carlo)
生成指定分布的随机数的抽样。
1. Markov Chain (马尔科夫链)
如果 f(t) 是一个时间序列,Markov Chain是如果f(t+1)仅仅与f(t)有关的随机过程。
Implement in R:
#author: rachel @ ZJU #email: [email protected] N = 10000 signal = vector(length = N) signal[1] = 0 for (i in 2:N) { # random select one offset (from [-1,1]) to signal[i-1] signal[i] = signal[i-1] + sample(c(-1,1),1) } plot( signal,type = 'l',col = 'red')
2. Random Walk(随机游走)
如布朗运动,仅仅是上面Markov Chain的二维拓展版:
Implement in R:
#author: rachel @ ZJU #email: [email protected] N = 100 x = vector(length = N) y = vector(length = N) x[1] = 0 y[1] = 0 for (i in 2:N) { x[i] = x[i-1] + rnorm(1) y[i] = y[i-1] + rnorm(1) } plot(x,y,type = 'l', col='red')
3. MCMC详细方法:
MCMC方法最早由Metropolis(1954)给出,后来Metropolis的算法由Hastings改进,合称为M-H算法。M-H算法是MCMC的基础方法。由M-H算法演化出了很多新的抽样方法,包含眼下在MCMC中最经常使用的Gibbs抽样也能够看做M-H算法的一个特例[2]。
概括起来,MCMC基于这种理论,在满足【平衡方程】(detailed balance equation)条件下,MCMC能够通过非常长的状态转移到达稳态。
3.1 M-H法
1. 构造目标分布,初始化x0
2. 在第n步,从q(y|x_n) 生成新状态y
3. 以一定概率((pi(y) * P(x_n|y)) / (pi(x) * P(y|x_n)))接受y <PS: 看看上面的平衡方程,这个概率表示什么呢?參考这里和[1]>
implementation in R:
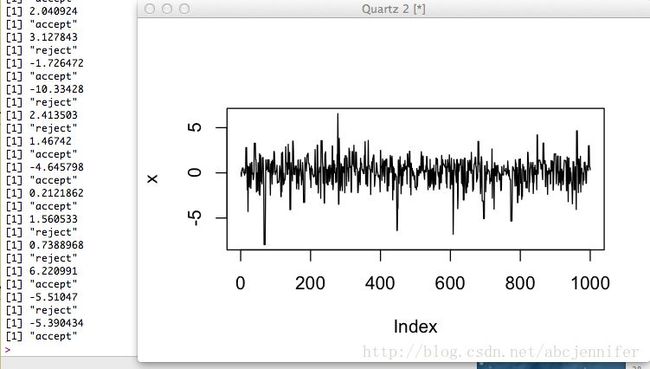
#author: rachel @ ZJU #email: [email protected] N = 10000 x = vector(length = N) x[1] = 0 # uniform variable: u u = runif(N) m_sd = 5 freedom = 5 for (i in 2:N) { y = rnorm(1,mean = x[i-1],sd = m_sd) print(y) y = rt(1,df = freedom) p_accept = dnorm(x[i-1],mean = y,sd = abs(2*y+1)) / dnorm(y, mean = x[i-1],sd = abs(2*x[i-1]+1)) #print (p_accept) if ((u[i] <= p_accept)) { x[i] = y print("accept") } else { x[i] = x[i-1] print("reject") } } plot(x,type = 'l') dev.new() hist(x)
3.2 Gibbs採样
那么在Gibbs採样中对其迭代採样的过程,实现例如以下:
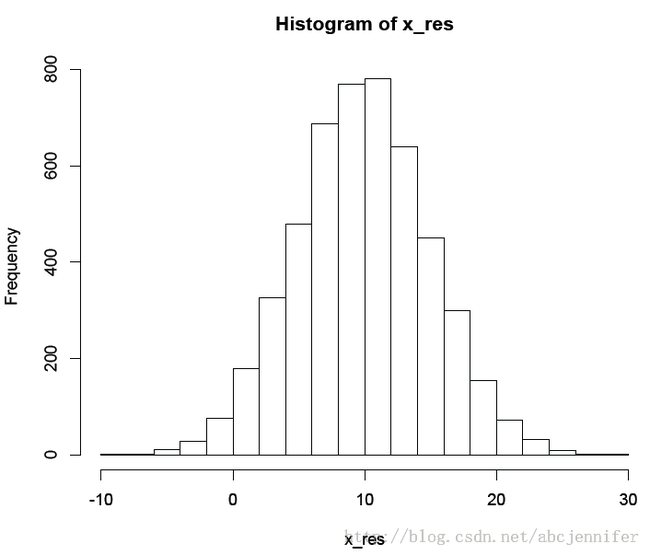
#author: rachel @ ZJU #email: [email protected] #define Gauss Posterior Distribution p_ygivenx <- function(x,m1,m2,s1,s2) { return (rnorm(1,m2+rho*s2/s1*(x-m1),sqrt(1-rho^2)*s2 )) } p_xgiveny <- function(y,m1,m2,s1,s2) { return (rnorm(1,m1+rho*s1/s2*(y-m2),sqrt(1-rho^2)*s1 )) } N = 5000 K = 20 #iteration in each sampling x_res = vector(length = N) y_res = vector(length = N) m1 = 10; m2 = -5; s1 = 5; s2 = 2 rho = 0.5 y = m2 for (i in 1:N) { x = p_xgiveny(y, m1,m2,s1,s2) y = p_ygivenx(x, m1,m2,s1,s2) # print(x) x_res[i] = x; y_res[i] = y; } hist(x_res,freq = 1) dev.new() plot(x_res,y_res) library(MASS) valid_range = seq(from = N/2, to = N, by = 1) MVN.kdensity <- kde2d(x_res[valid_range], y_res[valid_range], h = 10) #预计核密度 plot(x_res[valid_range], y_res[valid_range], col = "blue", xlab = "x", ylab = "y") contour(MVN.kdensity, add = TRUE)#二元正态分布等高线图 #real distribution # real = mvrnorm(N,c(m1,m2),diag(c(s1,s2))) # dev.new() # plot(real[1:N,1],real[1:N,2])
x分布图:
(x,y)分布图:
Reference:
1. http://www2.isye.gatech.edu/~brani/isyebayes/bank/handout10.pdf
2. http://site.douban.com/182577/widget/notes/10567181/note/292072927/
3. book: http://statweb.stanford.edu/~owen/mc/
4. Classic: http://cis.temple.edu/~latecki/Courses/RobotFall07/PapersFall07/andrieu03introduction.pdf
欢迎參与讨论并关注本博客和微博Rachel____Zhang, 兴许内容继续更新哦~