Codeforce 222 div1

A

假设只有一个连通块,任选一个点入队,按bfs/dfs序删除即可.

trick: 要考虑有多个连通块的情况,不一定无解.

 1 #define rep(i,n) for(int i=0 ; i<(n) ; i++)
 2 #define mid ((l+r)>>1)
 3 #define ls ((rt<<1))
 4 #define rs ((rt<<1)+1)
 5 #define maxn 510
 6 char g[maxn][maxn];
 7 bool vis[maxn][maxn];
 8 int n,m,k;
 9 struct node{
10     int r,c;
11 };queue<node> q;
12 struct src{
13     int size;
14     vector<node> ord;
15 };vector<src> p;
16 
17 int dr[] = {1,-1,0,0};
18 int dc[] = {0,0,1,-1};
19 
20 src bfs(int r,int c) {
21     src t;
22     t.ord.clear();
23     q.push((node){r,c});
24     vis[r][c]=true;
25     while (!q.empty()) {
26         node cur = q.front(),nxt; q.pop();
27         t.ord.push_back(cur);
28         rep (i,4) {
29             nxt.r = cur.r+dr[i];
30             nxt.c = cur.c+dc[i];
31             if (nxt.r<0||nxt.r>=n) continue;
32             if (nxt.c<0||nxt.c>=m) continue;
33             if (g[nxt.r][nxt.c]!='.') continue;
34             if (!vis[nxt.r][nxt.c]) {
35                 vis[nxt.r][nxt.c]=true;
36                 q.push(nxt);
37             }
38         }
39     }
40     t.size = t.ord.size();
41     return t;
42 }
43 
44 bool cmp(src a, src b) {
45     return a.size < b.size;
46 }
47 
48 void del(src t) {
49     for (int i=(int)t.ord.size()-1 ; i>=0 && k; i-- ) {
50         node cur = t.ord[i];
51         g[cur.r][cur.c] = 'X';
52         k--;
53     }
54 }
55 
56 int main() {
57 //    freopen("test","r",stdin);
58     scanf("%d%d%d",&n,&m,&k);
59     rep (i,n) scanf("%s",g[i]);
60     rep (i,n) rep (j,m) {
61         if (g[i][j]=='.' && !vis[i][j]) {
62             p.push_back(bfs(i,j));
63         }
64     }
65     sort(p.begin(),p.end(),cmp);
66     rep (i,(int)p.size()) {
67         if (!k) break;
68         del(p[i]);
69     }
70     rep (i,n) printf("%s\n",g[i]);
71     return 0;
72 }

View Code

 

B

 二分答案,然后对于给定的答案t,当然是让能力足够的student解决尽量多的问题,然后问题就转化为:

　　对于给定的ai,找到bj>=ai中c最小的元素

排序后用堆即可.

 1 #define rep(i,n) for(int i=0 ; i<(n) ; i++ )
 2 #define ls ((rt)<<1)
 3 #define rs (((rt)<<1)+1)
 4 #define mid ((l+r)>>1)
 5 #define maxn 100010
 6 #define INF 1000000100
 7 struct node{
 8     int b,c,id;
 9     bool operator < (const node &x) const{
10         return c>x.c;
11     }
12 };node stu[maxn];
13 int a[maxn],n,m,s,rcd[maxn],idx[maxn];
14 
15 priority_queue<node> q;
16 
17 bool cmp(node x,node y) {
18     return x.b>y.b;
19 }
20 
21 bool cmpa(int x,int y) {
22     return a[x]<a[y];
23 }
24 
25 void input() {
26     scanf("%d%d%d",&n,&m,&s);
27     rep (i,m) scanf("%d",a+i);
28     rep (i,n) scanf("%d",&stu[i].b);
29     rep (i,n) scanf("%d",&stu[i].c);
30     rep (i,n) stu[i].id = i+1;
31     rep (i,m) idx[i]=i;
32     stu[n] = (node){INF,INF,n};
33     sort(stu,stu+n+1,cmp);
34     sort(idx,idx+m,cmpa);
35 }
36 
37 int check(int t) {
38     while (!q.empty()) q.pop();
39     int cnts=0;
40     for (int i=m-1,j=0 ; i>=0 ; i-- ) {
41         while (j<=n && stu[j].b>=a[idx[i]]) {
42             q.push(stu[j++]);
43         }
44         node cur = q.top(); q.pop();
45         cnts += cur.c;
46         if (cnts>s) return 0;
47         rep (j,t) {
48             if (i-j>=0) rcd[idx[i-j]] = cur.id;
49             else return 1;
50         }
51         i -= (t-1);
52     }
53     return 1;
54 }
55 
56 int binsearch(int l,int r) {
57     while (true) {
58         if (l+1>=r) {
59             if (check(l)) return l;
60             if (check(r)) return r;
61             return -1;
62         }
63         if (check(mid)) r=mid;
64         else l=mid+1;
65     }
66 }
67 
68 int main(){
69 //    freopen("test.txt","r",stdin);
70     input();
71     int ans = binsearch(1,m);
72     if (ans==-1) printf("NO\n");
73     else {
74         printf("YES\n");
75         rep (i,m) printf("%d%c",rcd[i],i==m-1?'\n':' ');
76     }
77     return 0;
78 }

View Code

 

C

很容易地想到一个贪心做法:

　　将同一个队的连续选择一起考虑,那么可以先进行p操作,再进行b操作;

　　p操作当然选可选中体力最大的,b操作可以限制下一轮选择时对方体力增长,因此应当禁止体力最大的;

但这个做法是错误的因为下一轮对方可能没有p操作,最后轮到自己来选的时候发现体力大的被选走了...

正确的做法应该是在b操作的时候进行决策,好在m不大决策结果可以用mask表示.

所有操作都应该是针对前m大,所以mask表示前m大里面能选的集合即可.

 1 #define rep(i,n) for(int i=0 ; i<(n) ; i++ )
 2 #define ls ((rt)<<1)
 3 #define rs (((rt)<<1)+1)
 4 #define mid ((l+r)>>1)
 5 #define maxn 110
 6 #define mask (1<<20)
 7 #define INF 1000000000
 8 int dp[22][mask];
 9 int s[maxn],n,m;
10 struct node{
11     char c[2];
12     int id;
13 };node o[maxn];
14 
15 int dfs(int pos,int msk) {
16 
17     if (dp[pos][msk]!=INF) return dp[pos][msk];
18     if (pos==min(n,m)) return dp[pos][msk] = 0;
19 
20     if (o[pos].id==1) {
21         if (o[pos].c[0]=='p') {
22             rep (i,m) {
23                 if (!(msk&(1<<i))) {
24                     dp[pos][msk] = dfs(pos+1,msk|(1<<i)) + s[i];
25                     break;
26                 }
27             }
28         } else {
29             int tmp = -INF;
30             rep (i,m) {
31                 if (!(msk&(1<<i)))
32                     tmp = max(tmp,dfs(pos+1,msk|(1<<i)));
33             }
34             dp[pos][msk] = tmp;
35         }
36     } else {
37         if (o[pos].c[0]=='p') {
38             rep (i,m) {
39                 if (!(msk&(1<<i))) {
40                     dp[pos][msk] = dfs(pos+1,msk|(1<<i)) - s[i];
41                     break;
42                 }
43             }
44         } else {
45             int tmp = INF;
46             rep (i,m) {
47                 if (!(msk&(1<<i))) {
48                     tmp = min(tmp,dfs(pos+1,msk|(1<<i)));
49                 }
50             }
51             dp[pos][msk] = tmp;
52         }
53     }
54 //    printf("dp[%d][%d]=%d\n",pos,msk,dp[pos][msk]);
55     return dp[pos][msk];
56 }
57 
58 bool cmp(int x,int y) {return x>y;}
59 
60 int main(){
61 //    freopen("test.txt","r",stdin);
62     scanf("%d",&n);
63     rep (i,n) scanf("%d",s+i);
64     scanf("%d",&m);
65     rep (i,m) {
66         scanf("%s%d",o[i].c,&o[i].id);
67     }
68     sort(s,s+n,cmp);
69 //    rep (i,n) printf("%d ",s[i]); printf("\n");
70     rep (i,min(n,m)) rep (j,(1<<m)) dp[i][j]=INF;
71     printf("%d\n",dfs(0,0));
72     return 0;
73 }

View Code

 

D

问题可以描述为,求一个最大的集合所有元素满足:

　　max{l₀,l₁..} <= v₀,v₁,v₂... <= min{r₀,r₁}

因此,可以枚举l,它必定是某个3元组的l,并且是集合中最大的l,然后我们求出让答案最大的r:

　　(1)  max{ (l,l) , (l,l+1) , (l,l+2) ... }

现在l已经确定,只考虑所有li<=l的3元组:

　　(2)  每加入一个(li,vi,ri) , 它可以让 r属于[vi,ri] 的 询问增加1.

(1)是区间最值问题,(2)是成段更新问题,可以利用线段树实现.

接下来要考虑怎样枚举l,我们不希望每次枚举l都把3元组重新插入一次,这样复杂度太高.

可以先把所有3元组按l排序,按l单调增的顺序处理时,当考虑li的时候,之前插入的大部分还会被插入,部分应当被删除

现在考虑当l增加后,应当被删除的3元组:

　　(3) 所有v < li 的3元组都要删除.

可以发现,被某3元组被删除后,就没有机会再被插入了,另外(3)可以用对于v的小顶堆维护.

  1 typedef long long llong;
  2 #define rep(i,n) for(int i=0 ; i<(n) ; i++)
  3 #define mid ((l+r)>>1)
  4 #define ls ((rt<<1))
  5 #define rs ((rt<<1)+1)
  6 #define maxn 300010
  7 int big[maxn<<2],lz[maxn<<2],n;
  8 struct node{
  9     int l,v,r,id;
 10     bool operator < (const node& x) const {
 11         return v>x.v;
 12     }
 13 };node worker[maxn/3];
 14 priority_queue<node> q;
 15 
 16 bool cmp(node x,node y) {
 17     return x.l<y.l;
 18 }
 19 
 20 void input() {
 21     scanf("%d",&n);
 22     rep (i,n) {
 23         scanf("%d%d%d",&worker[i].l,&worker[i].v,&worker[i].r);
 24         worker[i].id = i+1;
 25     }
 26     sort(worker,worker+n,cmp);
 27 }
 28 
 29 void pushdown(int rt) {
 30     if (lz[rt]) {
 31         big[ls] += lz[rt];
 32         big[rs] += lz[rt];
 33         lz[ls] += lz[rt];
 34         lz[rs] += lz[rt];
 35         lz[rt] = 0;
 36     }
 37 }
 38 
 39 void pushup(int rt) {
 40     big[rt] = max(big[ls],big[rs]);
 41 }
 42 
 43 void add(int var,int L,int R,int l,int r,int rt) {
 44     if (L<=l && r<=R) {
 45         big[rt] += var;
 46         lz[rt] += var;
 47         return;
 48     }
 49     pushdown(rt);
 50     if (L<=mid) add(var,L,R,l,mid,ls);
 51     if (R>mid) add(var,L,R,mid+1,r,rs);
 52     pushup(rt);
 53 }
 54 
 55 int query(int L,int R,int l,int r,int rt) {
 56     int resl=0,resr=0;
 57     if (L<=l && r<=R) return big[rt];
 58     pushdown(rt);
 59     if (L<=mid) resl = query(L,R,l,mid,ls);
 60     if (R>mid) resr = query(L,R,mid+1,r,rs);
 61     pushup(rt);
 62     return max(resl,resr);
 63 }
 64 
 65 vector<int> rcd;
 66 void solv() {
 67     int ans=0,lft;
 68     rep (i,n) {
 69 //        printf("id:%d l:%d v:%d r:%d\n",worker[i].id,worker[i].l,worker[i].v,worker[i].r);
 70     }
 71     rep (i,n) {
 72         while (!q.empty()) {
 73             node tmp = q.top();
 74             if (tmp.v<worker[i].l) {
 75 //                printf("del:\nid:%d l:%d v:%d r:%d\n",tmp.id,tmp.l,tmp.v,tmp.r);
 76                 add(-1,tmp.v,tmp.r,0,maxn-1,1);
 77                 q.pop();
 78             } else break;
 79         }
 80         q.push(worker[i]);
 81 //        printf("add:\nid:%d l:%d v:%d r:%d\n",worker[i].id,worker[i].l,worker[i].v,worker[i].r);
 82         add(1,worker[i].v,worker[i].r,0,maxn-1,1);
 83         int tmp = query(worker[i].l,maxn-1,0,maxn-1,1);
 84 //        printf("cur ans: %d\n",tmp);
 85         if (tmp>ans) {
 86             ans = tmp;
 87             lft = i;
 88         }
 89     }
 90 
 91     while (!q.empty()) {
 92         node tmp = q.top(); q.pop();
 93         add(-1,tmp.v,tmp.r,0,maxn-1,1);
 94     }
 95 //    printf("\n\n");
 96 //    printf("lft:%d\n",lft);
 97     rep (i,lft+1) {
 98         while (!q.empty()) {
 99             node tmp = q.top();
100             if (tmp.v<worker[i].l) {
101     //            printf("del:\nid:%d l:%d v:%d r:%d\n",tmp.id,tmp.l,tmp.v,tmp.r);
102                 add(-1,tmp.v,tmp.r,0,maxn-1,1);
103                 q.pop();
104             } else break;
105         }
106         q.push(worker[i]);
107     //    printf("add:\nid:%d l:%d v:%d r:%d\n",worker[i].id,worker[i].l,worker[i].v,worker[i].r);
108         add(1,worker[i].v,worker[i].r,0,maxn-1,1);
109     }
110     for (int i=worker[lft].l ; i<maxn ; i++ ) {
111         int tmp = query(i,i,0,maxn-1,1);
112     //    printf("cur ans: %d\n",tmp);
113         if (tmp==ans) {
114             int L = worker[lft].l;
115             int R = i;
116     //        printf("L:%d R:%d\n",L,R);
117             while (!q.empty()) {
118                 node cur = q.top(); q.pop();
119     //            printf("id:%d l:%d v:%d r:%d\n",cur.id,cur.l,cur.v,cur.r);
120     //            printf("%d %d %d %d\n",L<=cur.v,cur.v<=R,cur.l<=L,cur.r>=R);
121                 if (L<=cur.v && cur.v<=R && cur.l<=L && cur.r>=R) {
122                     rcd.push_back(cur.id);
123                 }
124             }
125             return;
126         }
127     }
128 }
129 
130 int main() {
131 //    freopen("test","r",stdin);
132     input();
133     solv();
134     printf("%d\n",rcd.size());
135     rep (i,(int)rcd.size())
136         printf("%d%c",rcd[i],i==(int)rcd.size()-1?'\n':' ');
137     return 0;
138 }

View Code

 

E

 简单地说就是用一堆斜率上升的线段来表示 函数f(x):x时间能获得的最大收益,答案就是f(s).

 问题是如何维护表示f(x)的线段:

　　(1) 维护它的凸性:  

　　　　明显不会成为最优决策的building可以最先排除(先满足v单调,再满足c也单调);

　　　　每次买入新的building后,考虑它会比哪些更优,然后删除无用的;

　　　　这里有很多单调性,总之就是某个building被删除之后,绝对不会再成为最优决策了,所以可以这样维护;

　　(2) 对于新的building,找到最优决策;

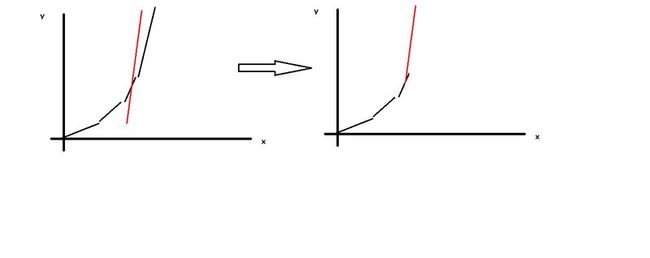
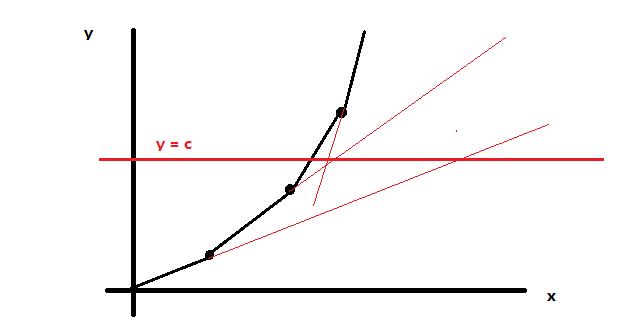
 因为(1)的作用,f(x)的形状是一个凸壳,做图可以发现,当新building与f(x)的交点t 小于某些顶点时, 该顶点以后的线段都可以删去,得到新的凸壳

 对于(2),想象一条直线 y=build.c 与f(x)相交 , 那么最优决策一定是f(x)所有直线方程中,交点最靠前的一条,如果从第一条开始枚举的话,时间t是单调减的,直到找到最优决策.

 又因为c保证了单调增,所以最优决策之前的线段都没有用了.

　　(1),(2)可以用双端队列维护.

 1 #define rep(i,n) for(int i=0 ; i<(n) ; i++ )
 2 #define ls ((rt)<<1)
 3 #define rs (((rt)<<1)+1)
 4 #define mid ((l+r)>>1)
 5 #define maxn 2000200
 6 #define INF 100000000000000000
 7 llong s;
 8 struct node{
 9     llong c,v;
10 };node build[maxn];
11 struct line{
12     llong v,d,t,X,Y;
13     llong f(llong x) {
14         if( (x-t)>=(INF+d)/v+1 ) return INF;
15         else return (x-t)*v+d;
16     }
17     llong x(llong y) {
18         return (y-d+v-1)/v+t;
19     }
20 };line seg[maxn];
21 
22 node use[maxn];
23 int n,tot,front,tail;
24 
25 bool cmp(node x,node y) {
26     return x.v<y.v;
27 }
28 
29 void input() {
30     scanf("%d%I64d",&n,&s);
31     build[0] = (node){0,1};
32     rep (i,n) {
33         scanf("%I64d%I64d",&build[i+1].v,&build[i+1].c);
34     }
35     build[n+1] = (node){s,INF};
36 }
37 
38 void pretreat() {
39     sort(build,build+n+2,cmp);
40     rep (i,n+2) {
41         if (i-1>=0 && build[i].v==build[i-1].v) continue;
42         while (tot && use[tot-1].c>=build[i].c) tot--;
43         use[tot++] = build[i];
44     }
45 }
46 
47 double findcross(line a,line b) {
48     double va,vb,ta,tb,da,db,x;
49     va = a.v;    vb = b.v;
50     ta = a.t;    tb = b.t;
51     da = a.d;    db = b.d;
52     x = (va*ta-vb*tb+db-da)/(va-vb);
53     return x;
54 }
55 
56 llong solv() {
57     seg[tail++] = (line){1,0,0,0,0};
58     rep (i,tot) {
59         while (tail-front>1 && seg[front].x(use[i].c) >= seg[front+1].x(use[i].c)) front++;
60         llong t = seg[front].x(use[i].c);
61         if (i==tot-1) return t;
62         line tmp = (line){use[i].v,seg[front].f(t)-use[i].c,t};
63         while (tail-front>1) {
64             if (findcross(seg[tail-2],seg[tail-1])>findcross(seg[tail-1],tmp)) tail--;
65             else break;
66         }
67         seg[tail++] = tmp;
68     }
69     return INF;
70 }
71 
72 int main(){
73 //    freopen("test.txt","r",stdin);
74     input();
75     pretreat();
76     llong ans = solv();
77     printf("%I64d\n",ans);
78     return 0;
79 }

View Code

 

　　(未知的bug,E题代码wa 13了....)