单源最短路径—Bellman-Ford和Dijkstra算法
Bellman-Ford算法：通过对边进行松弛操作来渐近地降低从源结点s到每个结点v的最短路径的估计值v.d，直到该估计值与实际的最短路径权重相同时为止。该算法主要是基于下面的定理：
设G=(V,E)是一带权重的源结点为s的有向图，其权重函数为W，假设图G中不包含从源结点s可到达的权重为负值的环路，在对图中的每条边执行|V|-1次松弛之后，对于所有从源结点s可到达的结点v，都有
。
证明：s可到达结点v并且图中没有权重为负值的环路，所以总能找到一条路径p=(v0,v1,...,vk)是从s到v结点的最短路径，这里v0=s，vk=v。因为最短路径都是简单路径，p最多包含|V|-1条边，即k<=|V|-1。由于v0=s，所以
，当对所有的边进行第1次松弛后，必有
，依次类推，进行第k次松弛后，必有
，最后可得进行|V|-1次松弛后有
下面证明为什么当
，对边
松弛后，有：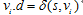
。
由于s->...->vi-1->vi是一条最短路径，在对边松弛后，
有：
(这个是松弛的定义)。
又由于
，所以：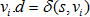
。
Bellman-Ford算法的实现是对图中的每条边进行|V|-1次松弛。
Dijkstra算法：将图中的结点分为两类，一类是结点集合S，从源结点s到集合中每个结点之间的最短路径已经被找到。另一类集合是V-S。算法重复地从集合V-S中选择最短路径估计最小的结点u，然后将u加入到集合S，然后对所有从u出发的边进行松弛。在进行|V|次重复操作后，其中每条边经历过一次松弛，对于所有的结点v，都有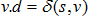
。关键点是证明：该算法在每次选择结点u来加入到集合S时，有
。证明过程省略，可以参考《算法导论》的证明过程。
下面给两种算法的出程序：在Dijkstra算法中，通过结点的颜色color来区分结点是属于S集合还是V-S集合，黑色时是S集合中，白色时是V-S集合中
Minpath.h
#pragma once
#include<iostream>
#include<string>
#include<vector>
using namespace std;
template<typename Comparable>
struct Edge;
template<typename Comparable>
struct Node
{
Comparable element;//结点的元素
vector<Edge<Comparable>*>Side;//该结点所在的边
Node<Comparable>* T; //最短路径中该结点的父亲
int dis; //距离
string color; //在Dijkstra算法中用于标记该结点是否被选中
Node(Comparable e,Node<Comparable>* f,int d,string c)
{
element=e;
T=f;
dis=d;
color=c;
}
};
template<typename Comparable>
struct Edge
{
Node<Comparable>* N1; //边的两端结点，N1是N2结点的父结点
Node<Comparable>* N2;
string color;
int weight;
Edge(Node<Comparable>* n1,Node<Comparable>* n2,int w):N1(n1),N2(n2),weight(w){}
};
template<typename Comparable>
class graph
{
public:
void insert(Comparable *a,int *matrix,int *w,int n);//a:图中个结点的元素；matrix:邻接矩阵
void Bellman(Comparable x);
void Dijkstra(Comparable x);
void MinPath(Comparable x);
private:
vector<Node<Comparable>*> root;
vector<Edge<Comparable>*> side;
Node<Comparable>* find(Comparable x);
Node<Comparable>* find();
void relax(Edge<Comparable>* edge); //松弛
void MinPath(Node<Comparable>* s);
};
Minpath.cpp
#include "stdafx.h"
#include"Minpath.h"
#include<iostream>
#include<string>
#include<vector>
using namespace std;
template<typename Comparable>
void graph<Comparable>::insert(Comparable *a,int *matrix,int *w,int n)
{
for(int i=0;i<n;i++)
{
Node<Comparable>* node=new Node<Comparable>(a[i],NULL,10000,"WHITE");
root.push_back(node);
}
Node<Comparable>* node=NULL;
Node<Comparable>* temp=NULL;
int k=0;
for(int i=0;i<n;i++)
{
node=root[i];
for(int j=0;j<n;j++)
{
if(matrix[n*i+j]!=0)
{
temp=root[j];
Edge<Comparable>* edge=new Edge<Comparable>(node,temp,w[k]);
k=k+1;
side.push_back(edge);
node->Side.push_back(edge);
}
}
}
}
//找出元素是x的结点
template<typename Comparable>
Node<Comparable>* graph<Comparable>::find(Comparable x)
{
int n=root.size();
Node<Comparable>* temp=NULL;
for(int i=0;i<n;i++)
{
if(root[i]->element==x)
temp=root[i];
}
return temp;
}
//边的松弛
template<typename Comparable>
void graph<Comparable>::relax(Edge<Comparable>* edge)
{
if(edge->N2->dis>edge->N1->dis+edge->weight)
{
edge->N2->dis=edge->N1->dis+edge->weight;
edge->N2->T=edge->N1;
}
}
//Bellman-Ford算法:对图中的边进行|v|-1次的松弛
template<typename Comparable>
void graph<Comparable>::Bellman(Comparable x)
{
Node<Comparable>* s=find(x);
bool flag=true;
if(s==NULL)
return;
int n=root.size();
int en=side.size();
Edge<Comparable>* edge=NULL;
s->dis=0; //选择s为源结点，并初始化其距离为0
//对图中的每个边进行|V|-1次的松弛
for(int i=0;i<n-1;i++)
{
for(int j=0;j<en;j++)
{
edge=side[j];
relax(edge); //松弛
}
}
for(int i=0;i<en;i++)
{
edge=side[i];
if(edge->N2->dis>edge->N1->dis+edge->weight)
flag=false;
}
if(flag==false)
cout<<"图中包含权重为负值的环路"<<endl;
else
{
s->T=NULL;
}
}
//Dijkstra算法
template<typename Comparable>
void graph<Comparable>::Dijkstra(Comparable x)
{
Node<Comparable>* s=find(x);
Node<Comparable>* source=s;
if(s==NULL)
return;
Edge<Comparable>* edge=NULL;
Node<Comparable>* temp=new Node<Comparable>(s->element,NULL,10000,"WHITE");
Node<Comparable>* t=temp;
int n=root.size();
s->dis=0;
s->color="BLACK"; //初始化源结点
for(int i=0;i<n;i++)
{
int en=s->Side.size();
for(int j=0;j<en;j++) //对s结点的所有的边进行一次松弛
{
edge=s->Side[j];
relax(edge);
}
s=find();
s->color="BLACK";
}
source->T=NULL;
}
template<typename Comparable>
Node<Comparable>* graph<Comparable>::find()
{
Node<Comparable>* s=new Node<Comparable>(root[0]->element,NULL,10000,"WHITE");
int n=root.size();
for(int i=0;i<n;i++)
{
if((root[i]->color=="WHITE")&&(root[i]->dis<s->dis))
s=root[i];
}
return s;
}
//找出某结点的最短路径并输出
template<typename Comparable>
void graph<Comparable>::MinPath(Comparable x)
{
Node<Comparable>* s=find(x);
cout<<"最短路径为："<<endl;
MinPath(s->T);
cout<<"("<<s->element<<","<<s->dis<<")"<<endl;
}
template<typename Comparable>
void graph<Comparable>::MinPath(Node<Comparable>* s)
{
if(s!=NULL)
{
MinPath(s->T);
cout<<"("<<s->element<<","<<s->dis<<")"<<"—>";
}
else
return;
}
Algorithm-graph3.cpp
// Algorithm-graph3.cpp : 定义控制台应用程序的入口点。
//主要是图中的最短路径问题：Bellman-Ford算法和Dijkstra算法
#include "stdafx.h"
#include"Minpath.h"
#include"Minpath.cpp"
#include<iostream>
#include<string>
#include<vector>
using namespace std;
#include<iostream>
int _tmain(int argc, _TCHAR* argv[])
{
graph<string> g;
////Bellman-Ford算法
/* int n=5;
int matrix[25]={0,1,0,0,1,
0,0,1,1,1,
0,1,0,0,0,
1,0,1,0,0,
0,0,1,1,0};
string a[5]={"s","t","x","z","y"};
int w[10]={6,7,5,-4,8,-2,2,7,-3,9};*/
//Dijkstra算法
int n=5;
int matrix[25]={0,1,0,0,1,
0,0,1,0,1,
0,0,0,1,0,
1,0,1,0,0,
0,1,1,1,0};
string a[5]={"s","t","x","z","y"};
int w[10]={10,5,1,2,4,7,6,3,9,2};
g.insert(a,matrix,w,n);
// g.Bellman("s");
g.Dijkstra("s"); //选择结点元素为s的作为源结点
g.MinPath("x"); //输出结点元素是x的最短路径
return 0;
}