A Knight's Journey(dfs)

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 25950		Accepted: 8853

Description

Background 
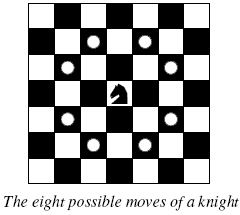
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3

1 1

2 3

4 3

Sample Output

Scenario #1:

A1



Scenario #2:

impossible



Scenario #3:

A1B3C1A2B4C2A3B1C3A4B2C4

题意：给出p和q,p代表行数（1，2,3....）,q代表列数（A,B,C....）,要求输出骑士从任意一点出发经过所有点的路径，必须按字典序输出；路径不存在输出impossible；

思路：与dfs模板不同的是路径按字典序输出，所以dfs的顺序就不是随意的了，必须按dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}}的顺序；
     而且起点必须是A1,这样得出的路径字典序才最小；

 1 #include<iostream>

 2 #include<stdio.h>

 3 #include<string.h>

 4 using namespace std;

 5 

 6 struct node

 7 {

 8     int row;

 9     int col;

10 }way[30];//记录所走路径的行和列

11 

12 int p,q;

13 bool vis['Z'+1][27];

14 int dir[8][2] = {{-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,1},{-1,2},{1,2}};

15 

16 bool DFS(struct node* way,int i,int j,int step)

17 {

18     vis[i][j]=true;

19     way[step].row=i;

20     way[step].col=j;

21     if(step==way[0].row)

22         return true;

23 

24     for(int k=0; k<8; k++)//向八个方向走

25     {

26         int ii = i+dir[k][0];

27         int jj = j+dir[k][1];

28         if(!vis[ii][jj] && ii>=1 && ii<=p && jj>=1 && jj<=q)

29             if(DFS(way,ii,jj,step+1))

30                 return true;

31     }

32 

33     vis[i][j]=false;

34     return false;

35 }

36 

37 int main()

38 {

39     int test;

40     scanf("%d",&test);

41     for(int t = 1; t <= test; t++)

42     {

43         memset(vis,false,sizeof(vis));

44         scanf("%d %d",&p,&q);

45        

46         way[0].row =p*q;

47 

48         if(DFS(way,1,1,1))

49         {

50             cout<<"Scenario #"<<t<<':'<<endl;

51 

52             for(int k=1; k<=way[0].row; k++)

53                 cout<<(char)(way[k].col-1+'A')<<way[k].row;

54             cout<<endl<<endl;

55 

56         }

57 

58         else

59         {

60             cout<<"Scenario #"<<t<<':'<<endl;

61             cout<<"impossible"<<endl<<endl;

62         }

63     }

64     return 0;

65 }

View Code