有向图强连通分量

部分转自

[有向图强连通分量]

有向图中，如果一个子图内任意两点都可达这这个子图为强连通子图

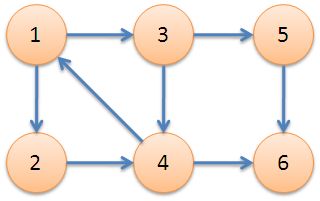
如图所示{1, 2，3，4}，{5}，{6} 为一个强连通子图

求连通分量

1.用Kosaraju算法（PS：个人感觉Kosaraju算法比较好理解，但是适用范围不如Tarjan算法广）

如果在原图中点 i 可达 点 j

如果图逆向之后，i 依然可以达到 j ，这么可以认为 i 和 j 在同一个强连通分量里

具体算法是

1.先对图进行一次DFS进行标号确定逆向图进行搜索的次序，越接近图的尾部（搜索树的叶子），顶点标号越小

2.逆向搜索从标号最大的进行搜索，再次进行DFS，把每次DFS可达的点进行相同的标记，那么标记相同的点就在一个强连通子图中。

 

int n; //结点个数

vector<int>graph[MAXN]; //用邻接表表示图

vector<int>rgraph[MAXN]; //图的反向

vector<int>vs;  //用来记录进行逆向图搜索的次序

bool vis[MAXN]; //标记是否访问

int cmp[MAXN]; //记录联通图



void add_edge(int v,int u){ //向图中加边

    graph[v].push_back(u);  //正向图

    rgraph[u].push_back(v); // 逆向图

    return;

}

void dfs(int v){ //进行正向图的第一次搜索

    vis[v] = 1;

    int s = graph[v].size();

    for(int i = 0;i < s;i++){

        int u = graph[v][i];

        if(!vis[u]){

            dfs(u);

        }

    }

    vs.push_back(v); //确定次序

}

void rdfs(int v,int k){  //第二次对逆向图搜索

    vis[v] = 1;

    cmp[v] = k; //记录可达的点

    int s = rgraph[v].size();

    for(int i = 0;i < s;i++){

        int u = rgraph[v][i];

        if(!vis[u]){

            rdfs(u,k);

        }

    }

}

int scc(){

    memset(vis,0,sizeof(vis)); //初始化

    vs.clear();

    for(int i = 0;i < n;i++){

        if(!vis[i]){

            dfs(i);

        }

    }

    memset(vis,0,sizeof(vis));

    int k = 0;

    int s = vs.size(); //从最大的标号搜素

    for(int i = s-1;i > -1;i--){

        if(!vis[ vs[i] ]){

            rdfs(vs[i],k++);

        }

    }

    return k; //连通分量个数

}

 

2. Tarjan算法 （之前的链接已经很棒了）

只写一下个人理解

搬图……！！！！

DFN 为 搜索次序，LOW[u] 是 u 可达的点中 最小的 DFN 值 当 DFN[u] == LOW[u]（意味着它通过某条路回到了曾走过的点，说明这两点任意可达） 时 以u 为根的搜索子树上所有节点是一个强连通分量

所以如图 点 6 是一个强连通分量

而这张图 点 4 可达 点 1 所以 LOW[4] = 1 ，而 点3 是点 4 的父节点 所以 LOW[3] = LOW[4] = 1; LOW[1] = DFN[1]

所以目前{1，3，4}在一个强连通图中，下一阶段就是进行 1 → 2的搜索 点 2 也在该连通子图中

代码（抄的维基）

const int MAXN = 100000 + 10; //最大结点的个数

int STACK[MAXN]; //用来记录一次搜索中，把搜索过的元素入栈

int top; //栈顶指针

bool InStack[MAXN];//用来标记元素是否在栈中

int DFN[MAXN];  //搜索次序

int LOW[MAXN];  //该节点所能到达的最小次序

int Index; //次序编号

int componentnumber; //连通分量个数

vector<int>edge[MAXN]; //图邻接表

vector<int>component[MAXN]; //每个连通分量中所包含的点

int incomponent[MAXN]; //在一个强连通子图中的标记是一样的

int n;

void Tarjan(int i){ //算法

    int j; 

    DFN[i] = LOW[i] = Index++; //首先默认本身为一个强连通分量

    STACK[++top] = i; // i 点被搜索过入栈

    InStack[i] = 1; //入栈元素标记

    int s = edge[i].size();

    for(int e = 0;e < s;e++){

        j = edge[i][e];

        if(DFN[j] == -1){ //如果没有被搜索过

            Tarjan(j); //进行搜索

            LOW[i] = min(LOW[i],LOW[j]); //LOW[i] 对其可达的最小编号进行更新

        }

        else if(InStack[j]){ //如果已经搜索过

            LOW[i] = min(LOW[i],DFN[j]); //对LOW[i]进行更新

        }

    }

    if(DFN[i] == LOW[i]){ //如果最后 i 点通过某条路又回到了自身，说明走过的路是一个强连通子图

        componentnumber++; //连通分量的个数加1

        do{

            j = STACK[top--];  //栈中是访问的点

            InStack[j] = 0;//清零

            component[componentnumber].push_back(j); //记录

            incomponent[j] = componentnumber; //记录

        }

        while(j != i);

    }

    return;

}

void solve(){

    memset(STACK,-1,sizeof(STACK)); //初始化

    memset(InStack,0,sizeof(InStack));

    memset(DFN,-1,sizeof(DFN));

    memset(LOW,-1,sizeof(LOW));

    ans = -1;

    top = 0;

    Index = 0;

    componentnumber = 0;

    for(int i = 0;i <= n;i++){

        component[i].clear();

    }

    for(int i = 0;i < n;i++){

        if(DFN[i] == -1){

            Tarjan(i);

        }

    }

    return;

}

 

题目链接：http://poj.org/problem?id=2186

#include <iostream>

#include <cstdio>

#include <cstring>

#include <cstdlib>

#include <cmath>

#include <string>

#include <queue>

#include <stack>

#include <algorithm>

#include <map>

#include <set>



const int MAXN = 10000 + 10;

const int MOD = 10000007;

const int INF = 0x7fffffff;

const double Pi = acos(-1.0);

const double ESP = 10e-8;



using namespace std;

int n;

vector<int>graph[MAXN];

vector<int>rgraph[MAXN];

vector<int>vs;

bool vis[MAXN];

int cmp[MAXN];

void add_edge(int v,int u){

    graph[v].push_back(u);

    rgraph[u].push_back(v);

    return;

}

void dfs(int v){

    vis[v] = 1;

    int s = graph[v].size();

    for(int i = 0;i < s;i++){

        int u = graph[v][i];

        if(!vis[u]){

            dfs(u);

        }

    }

    vs.push_back(v);

}

void rdfs(int v,int k){

    vis[v] = 1;

    cmp[v] = k;

    int s = rgraph[v].size();

    for(int i = 0;i < s;i++){

        int u = rgraph[v][i];

        if(!vis[u]){

            rdfs(u,k);

        }

    }

}

int scc(){

    memset(vis,0,sizeof(vis));

    vs.clear();

    for(int i = 0;i < n;i++){

        if(!vis[i]){

            dfs(i);

        }

    }

    memset(vis,0,sizeof(vis));

    int k = 0;

    int s = vs.size();

    for(int i = s-1;i > -1;i--){

        if(!vis[ vs[i] ]){

            rdfs(vs[i],k++);

        }

    }

    return k;

}

void solve(int m){

    for(int i = 0;i <= n;i++){

        graph[i].clear();

        rgraph[i].clear();

    }

    while(m--){

        int a,b;

        scanf("%d%d",&a,&b);

        add_edge(a-1,b-1);

    }

    int x = scc();

    int num = 0;

    int u = 0;

    for(int i = 0;i < n;i++){

        if(cmp[i] == x-1){

            u = i;

            num++;

        }

    }

    memset(vis,0,sizeof(vis));

    rdfs(u,0);

    for(int i = 0;i < n;i++){

        if(!vis[i]){

            num = 0;

            break;

        }

    }

    printf("%d\n",num);

}

int main(){

//    freopen("input.txt","r",stdin);

    int m;

    while(~scanf("%d%d",&n,&m)){

        solve(m);

    }

    return 0;

}

View Code