HDU 3507 Print Article（单调队列）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3507

题意：给出一个数列C，一个数字M，将数列分成若干段，每段的代价为（设这段的数字为k个）：

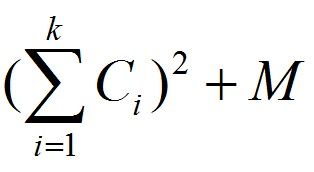
求一种分法使得总代价最小？

思路:dp[i]=min(dp[j]+sqr(sum[i]-sum[j])+M)。对于两个j1,j2，设j1<j2，若j2比j1优，那么可得：(dp[j1]+sqr(sum[j1]))-(dp[j2]+sqr(sum[j2]))>=sum[i]*2*(sum[j1]-sum[j2])。令dy(j1,j2)=(dp[j1]+sqr(sum[j1]))-(dp[j2]+sqr(sum[j2])),dx(j1,j2)=2*(sum[j1]-sum[j2])，每次令j1=Q[head],j2=Q[head+1],比较dy(j1,j2)和sum[i]*dx(j1,j2)可判定head的优还是head+1的优。队尾的三个x,y,z，若dy(x,y)*dx(y,z)>=dy(y,z)*dx(x,y)，则y可以删去。

#include <iostream>

#include <stdio.h>

#include <string.h>

#include <algorithm>

#include <cmath>

#include <vector>

#include <queue>

#include <set>

#include <stack>

#include <string>

#include <map>





#define max(x,y) ((x)>(y)?(x):(y))

#define min(x,y) ((x)<(y)?(x):(y))

#define abs(x) ((x)>=0?(x):-(x))

#define i64 long long

#define u32 unsigned int

#define u64 unsigned long long

#define clr(x,y) memset(x,y,sizeof(x))

#define CLR(x) x.clear()

#define ph(x) push(x)

#define pb(x) push_back(x)

#define Len(x) x.length()

#define SZ(x) x.size()

#define PI acos(-1.0)

#define sqr(x) ((x)*(x))

#define MP(x,y) make_pair(x,y)

#define EPS 1e-9



#define FOR0(i,x) for(i=0;i<x;i++)

#define FOR1(i,x) for(i=1;i<=x;i++)

#define FOR(i,a,b) for(i=a;i<=b;i++)

#define FORL0(i,a) for(i=a;i>=0;i--)

#define FORL1(i,a) for(i=a;i>=1;i--)

#define FORL(i,a,b)for(i=a;i>=b;i--)





#define rush() int CC;for(scanf("%d",&CC);CC--;)

#define Rush(n)  while(scanf("%d",&n)!=-1)

using namespace std;





void RD(int &x){scanf("%d",&x);}

void RD(u32 &x){scanf("%u",&x);}

void RD(i64 &x){scanf("%I64d",&x);}

void RD(double &x){scanf("%lf",&x);}

void RD(int &x,int &y){scanf("%d%d",&x,&y);}

void RD(u32 &x,u32 &y){scanf("%u%u",&x,&y);}

void RD(double &x,double &y){scanf("%lf%lf",&x,&y);}

void RD(int &x,int &y,int &z){scanf("%d%d%d",&x,&y,&z);}

void RD(int &x,int &y,int &z,int &t){scanf("%d%d%d%d",&x,&y,&z,&t);}

void RD(u32 &x,u32 &y,u32 &z){scanf("%u%u%u",&x,&y,&z);}

void RD(double &x,double &y,double &z){scanf("%lf%lf%lf",&x,&y,&z);}

void RD(char &x){x=getchar();}

void RD(char *s){scanf("%s",s);}

void RD(string &s){cin>>s;}





void PR(int x) {printf("%d\n",x);}

void PR(int x,int y) {printf("%d %d\n",x,y);}

void PR(int x,int y,int z) {printf("%d %d %d\n",x,y,z);}

void PR(i64 x) {printf("%lld\n",x);}

void PR(u32 x) {printf("%u\n",x);}

void PR(double x) {printf("%.5lf\n",x);}

void PR(char x) {printf("%c\n",x);}

void PR(char *x) {printf("%s\n",x);}

void PR(string x) {cout<<x<<endl;}





const int INF=1000000000;

const int N=500005;



int n,m,Q[N],head,tail;

i64 sum[N],dp[N],a[N];



i64 dy(int j1,int j2)

{

	return (dp[j1]+sum[j1]*sum[j1])-(dp[j2]+sum[j2]*sum[j2]);

}



i64 dx(int j1,int j2)

{

	return 2*(sum[j1]-sum[j2]);

}



void DP()

{

	int i,j,x,y,z;



	head=tail=0;

	FOR1(i,n)

	{

		while(head<tail&&dy(Q[head],Q[head+1])>=sum[i]*dx(Q[head],Q[head+1])) head++;

		j=Q[head];

		dp[i]=dp[j]+sqr(sum[i]-sum[j])+m;

		z=i;

        while(head<tail)

        {

            x=Q[tail-1];

            y=Q[tail];

            if(dy(x,y)*dx(y,z)>=dy(y,z)*dx(x,y)) tail--;

            else break;

        }

        Q[++tail]=z;

	}

	PR(dp[n]);

}



int main()

{

    Rush(n)

    {

        RD(m);

        int i;

        FOR1(i,n) RD(a[i]),sum[i]=sum[i-1]+a[i];

        DP();

    }

	return 0;

}