ZOJ 3256 Tour in the Castle(插头DP-按行递推—矩阵)

题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3540

题意：给出一个n*m的方格。从左上角走到左下角每个格子只能走一次。有多少种？

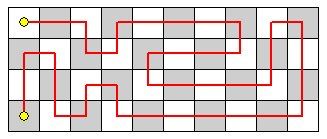
思路：首先，按行递推，得到一个矩阵，表示两个状态是否可以连接。那么最关键的判断两行是否可连接。上一行的一个状态，枚举当前行的插头的状态,就是有无插头，2^n，然后根据上一行的插头的连通性判断当前行插头的连通性。

#include <iostream>

#include <cstdio>

#include <string.h>

#include <algorithm>

#include <cmath>

#include <vector>

#include <queue>

#include <set>

#include <stack>

#include <string>

#include <map>





#define max(x,y) ((x)>(y)?(x):(y))

#define min(x,y) ((x)<(y)?(x):(y))

#define abs(x) ((x)>=0?(x):-(x))

#define i64 long long

#define u32 unsigned int

#define u64 unsigned long long

#define clr(x,y) memset(x,y,sizeof(x))

#define CLR(x) x.clear()

#define ph(x) push(x)

#define pb(x) push_back(x)

#define Len(x) x.length()

#define SZ(x) x.size()

#define PI acos(-1.0)

#define sqr(x) ((x)*(x))



#define FOR0(i,x) for(i=0;i<x;i++)

#define FOR1(i,x) for(i=1;i<=x;i++)

#define FOR(i,a,b) for(i=a;i<=b;i++)

#define FORL0(i,a) for(i=a;i>=0;i--)

#define FORL1(i,a) for(i=a;i>=1;i--)

#define FORL(i,a,b)for(i=a;i>=b;i--)





#define rush() int C; for(scanf("%d",&C);C--;)

#define Rush(n)  while(scanf("%d",&n)!=-1)

using namespace std;





void RD(int &x){scanf("%d",&x);}

void RD(i64 &x){scanf("%lld",&x);}

void RD(u32 &x){scanf("%u",&x);}

void RD(double &x){scanf("%lf",&x);}

void RD(int &x,int &y){scanf("%d%d",&x,&y);}

void RD(u32 &x,u32 &y){scanf("%u%u",&x,&y);}

void RD(double &x,double &y){scanf("%lf%lf",&x,&y);}

void RD(int &x,int &y,int &z){scanf("%d%d%d",&x,&y,&z);}

void RD(u32 &x,u32 &y,u32 &z){scanf("%u%u%u",&x,&y,&z);}

void RD(double &x,double &y,double &z){scanf("%lf%lf%lf",&x,&y,&z);}

void RD(char &x){x=getchar();}

void RD(char *s){scanf("%s",s);}

void RD(string &s){cin>>s;}



void PR(int x) {printf("%d\n",x);}

void PR(i64 x) {printf("%lld\n",x);}

void PR(u32 x) {printf("%u\n",x);}

void PR(double x) {printf("%.4lf\n",x);}

void PR(char x) {printf("%c\n",x);}

void PR(char *x) {printf("%s\n",x);}

void PR(string x) {cout<<x<<endl;}





const int mod=7777777;

const int INF=1000000000;

const int HASHSIZE=100007;

const int N=1000005;





int n,m,code[15],a[130][130],D;



class Matrix

{

public:

    int a[130][130];



    Matrix operator*(Matrix p)

    {

        int i,j,k;

        i64 temp;

        Matrix ans;

        FOR0(i,D) FOR0(j,D)

        {

            temp=0;

            FOR0(k,D) temp+=(i64)a[i][k]*p.a[k][j];

            ans.a[i][j]=temp%mod;

        }

        return ans;

    }

};



Matrix p,q;





struct node

{

    int e,next[N],head[HASHSIZE],state[N];



    void init()

    {

        clr(head,-1);

        e=0;

    }



    int push(int s)

    {

        int i,x=s%HASHSIZE;

        for(i=head[x];i!=-1;i=next[i])

        {

            if(state[i]==s) return i;

        }

        state[e]=s;

        next[e]=head[x];

        head[x]=e++;

        return e-1;

    }

};





node dp;



void decode(int code[],int m,int st)

{

    int i;

    FORL0(i,m-1) code[i]=st&3,st>>=2;

}



int encode(int code[],int m)

{

    int ans=0,hash[100],i,cnt=1;

    clr(hash,-1);

    hash[0]=0;

    FOR0(i,m)

    {

        if(hash[code[i]]==-1) hash[code[i]]=cnt++;

        code[i]=hash[code[i]];

        ans=(ans<<2)|code[i];

    }

    return ans;

}







int OK(int st1,int st2)

{

    decode(code,n,st1);

    int i,j,k,flag=0,cnt=n,temp;

    FOR0(i,n)

    {

        if(!flag)

        {

            if(!code[i]&&!(st2&(1<<i))) return 0;

            if(code[i]&&(st2&(1<<i))) continue;

            if(code[i]) flag=code[i];

            else flag=-1;

            k=i;

        }

        else

        {

            if(code[i]&&(st2&(1<<i)))return 0;

            if(!code[i]&&!(st2&(1<<i))) continue;

            if(code[i])

            {

                if(code[i]==flag)

                {

                    if(!(st2==0&&i==n-1)) return 0;

                }

                if(flag>0)

                {

                    temp=code[i];

                    FOR0(j,n) if(code[j]==temp) code[j]=code[k];

                    code[i]=code[k]=0;

                }

                else code[k]=code[i],code[i]=0;

            }

            else

            {

                if(flag>0) code[i]=code[k],code[k]=0;

                else code[i]=code[k]=cnt++;

            }

            flag=0;

        }

    }

    if(flag) return 0;

    return 1;

}





void init()

{

    dp.init(); dp.push(0); clr(code,0);

    code[0]=code[n-1]=1; dp.push(encode(code,n));

    clr(a,0);

    int i,j,k;

    FOR1(i,dp.e-1)

    {

        FOR0(j,(1<<n)) if(OK(dp.state[i],j))

        {

            k=dp.push(encode(code,n));

            a[i][k]=1;

        }

    }

    D=dp.e;

}



int main()

{

    Rush(n)

    {

        RD(m); init(); clr(p.a,0);

        int i,j;

        FOR0(i,D) p.a[i][i]=1;

        FOR0(i,D) FOR0(j,D) q.a[i][j]=a[i][j];

        while(m)

        {

            if(m&1) p=p*q;

            q=q*q;

            m>>=1;

        }

        if(p.a[1][0]) PR(p.a[1][0]);

        else puts("Impossible");

    }

    return 0;

}