Chp11: Sorting and Searching

Common Sorting Algo:

Bubble Sort: Runime: O(n2) average and worst case. Memory: O(1).

1 void BubbleSortArray(){ 

2     for(int i=1;i<n;i++)

3         for(int j=0;i<n-i;j++) 

4             if(a[j]>a[j+1]){//比较交换相邻元素  

5                int temp; 

6                temp=a[j]; a[j]=a[j+1]; a[j+1]=temp; 

7     } 

8 } 

Selection Sort: Runtime: O(n2) average and worst case. Memory: O(1).

 1 void SelectSortArray(){ 

 2     int min_index; 

 3     for(int i=0;i<n-1;i++){ 

 4          min_index=i; 

 5          for(int j=i+1;j<n;j++)//每次扫描选择最小项 

 6             if(arr[j]<arr[min_index])  min_index=j; 

 7          if(min_index!=i){//找到最小项交换，即将这一项移到列表中的正确位置 

 8              int temp; 

 9              temp=arr[i]; arr[i]=arr[min_index]; arr[min_index]=temp; 

10         } 

11     } 

12 } 

Merge Sort: Runtime: O(nlogn) average and worst case. Memory: Depends.

 1 void mergeSort(int[] array, int low,int high){

 2     if(low < high){

 3         int middle = (low + high) / 2;

 4         mergeSort(array, low, middle);

 5         mergeSort(array, middle + 1, high);

 6         merge(array, low, middle, high);

 7     }

 8 }

 9 void merge(int[] array, int low, int middle, int high){

10     int[] helper = new int[array.length];

11     for(int i = low; i <= high; i ++)

12         helper[i] = array[i];

13     int helperLeft = low;

14     int helperRight = middle + 1;

15     int current = low;

16     while(helperLeft <= middle && helperRight <= high){

17         if(helper[helperLeft] <= helper[helperRight])

18             array[current ++] = helper[helperLeft ++];

19         else

20             array[current ++] = helper[helperRight ++];

21     }

22     int remaining = middle - helperLeft;

23     for(int i = 0; i <= remaining; i ++)

24         array[current + i] = helper[helperLeft + i];

25 }

Quick Sort: Runtime: O(nlogn) average, O(n2) worse case. Memory: O(nlogn).

In quick sort, we pick a random element and partition the array, such that all numbers that are less than the partitioning element come before all elements that are greater than it. The partitioning can be performed efficiently through a series of swaps.

 1 void quickSort(int[] arr, int left, int right){

 2     int index = partition(arr, left, right);

 3     if(left < index - 1) quickSort(arr, left, index - 1);

 4     if(right < index - 1) quickSort(arr, index, right);

 5 }

 6 int partition(int[] arr, int left, int right){

 7     int pivot = arr[(left + right) / 2];

 8     while(left <= right){

 9         while(arr[left] < pivot) left ++;

10         while(arr[right] > pivot) right --;

11         if(left <= right){

12             swap(arr, left, right);

13             left ++;

14             right --;

15         }

16     }

17     return left;

18 }

 1 //pro4 : quick sort

 2     public int adjust_array(int[] input,int low,int high){

 3         //set the pivot to be the first element of the array

 4         int pivot = input[low];

 5         int exchange = 0;

 6         while(low < high){

 7             //from the tail to header,find the item smaller than the pivot 

 8             while(input[high] >= pivot && high > low)

 9                 high --;

10             exchange = input[high];

11             input[high] = input[low];

12             input[low] = exchange;

13             //from the header to tail,find the item larger than the pivot

14             while(input[low] <= pivot && high > low)

15                 low ++;

16             exchange = input[high];

17             input[high] = input[low];

18             input[low] = exchange;

19         }

20         //set the mid to be pivot

21         input[low] = pivot;

22         

23         return low;

24     }

25 

26     public void quick_sort(int[] input, int low, int high){

27         //set the low and high pointer

28         if(low < high){

29             int mid = adjust_array(input,low,high);

30             quick_sort(input, 0, mid - 1);

31             quick_sort(input, mid + 1, high);

32         }

33     }

34     

35     public void pro4(){

36         int[] input = {20,1,2,40,7,90,11};

37         int low = 0;

38         int high = input.length - 1;

39         quick_sort(input,low,high);

40         for(int i = 0; i < input.length; i ++){

41             System.out.println(input[i]);

42         }

43     }

 

Radix Sort: Runtime: O(kn).

It is a sorting algo for intergers that takes advantage of the fact that integers have a finite number of bits.

 1 Void RadixSort(Node L[],length,maxradix)

 2 {

 3     Int m,n,k,lsp;

 4     k=1;m=1;

 5     Int temp[10][length-1];

 6     Empty(temp); //清空临时空间

 7     While(k<maxradix) //遍历所有关键字

 8     {

 9         For(int i=0;i<length;i++) //分配过程

10         {

11             If(L[i]<m)

12             Temp[0][n]=L[i];

13             Else

14             Lsp=(L[i]/m)%10; //确定关键字

15             Temp[lsp][n]=L[i];

16             n++;

17         }

18         CollectElement(L,Temp); //收集

19         n=0;

20         m=m*10;

21         k++;

22     }

23 }

Bucket sort:

Bucket sort, or bin sort, is a sorting algorithm that works by partitioning an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, and is a cousin of radix sort in the most to least significant digit flavour. Bucket sort is a generalization of pigeonhole sort. Since bucket sort is not a comparison sort, the Ω(n log n) lower bound is inapplicable. The computational complexity estimates involve the number of buckets.

Bucket sort works as follows:

1. Set up an array of initially empty "buckets."
2. Scatter: Go over the original array, putting each object in its bucket.
3. Sort each non-empty bucket.
4. Gather: Visit the buckets in order and put all elements back into the original array.

Pseudocode

function bucketSort(array, n) is

  buckets ← new array of n empty lists

  for i = 0 to (length(array)-1) do

    insert array[i] into buckets[msbits(array[i], k)]

  for i = 0 to n - 1 do

    nextSort(buckets[i])

  return the concatenation of buckets[0], ...., buckets[n-1]

Here array is the array to be sorted and n is the number of buckets to use. The function msbits(x,k) returns the k most significant bits of x (floor(x/2^(size(x)-k))); different functions can be used to translate the range of elements in array to n buckets, such as translating the letters A–Z to 0–25 or returning the first character (0–255) for sorting strings. The function nextSort is a sorting function; using bucketSort itself as nextSort produces a relative of radix sort; in particular, the case n = 2 corresponds toquicksort (although potentially with poor pivot choices).

Heap Sort: Runtime:O(nlgn) average and worse case.

 1 //堆排序 

 2 template 

 3 void Sort::HeapSort(T* array, int size) 

 4 { 

 5     int lastP = size / 2; 

 6     //从最后一个有孩子的结点开始建初始堆 

 7     for(int i = lastP - 1; i >= 0; i--) 

 8     { 

 9         HeapAjust(array, i, size); 

10     } 

11     int j = size; 

12     //将堆顶元素和无序区间的最后一个元素交换，再调整堆 

13     while(j > 0) 

14     { 

15         Swap(array, 0, j - 1); 

16         j--; 

17         HeapAjust(array, 0, j); 

18     } 

19 } 

20 //调整堆 

21 template 

22 void Sort::HeapAjust(T *array, int toAjust, int size) 

23 { 

24     int pos = toAjust; 

25     while((pos * 2 + 1) < size) 

26     { 

27         int lChild = pos * 2 + 1; 

28         if(array[lChild] > array[pos]) 

29         { 

30             pos = lChild;//左孩子大 

31         } 

32         int rChild = lChild + 1; 

33         if(rChild < size && array[rChild] > array[pos]) 

34         { 

35             pos = rChild;//右孩子更大 

36         } 

37         if(pos != toAjust) //父结点比其中一个孩子小 

38         { 

39             Swap(array, toAjust, pos); 

40             toAjust = pos; 

41         } 

42         else 

43         { 

44             break; 

45         } 

46     } 

47 }

Insertion Sort: Runtime O(n2).

 1 //插入排序 

 2 template 

 3 void Sort::InsertSort(T* array, int size) 

 4 { 

 5     for(int i = 1; i < size; i++) 

 6     { 

 7         for(int j = i; j > 0; j--) 

 8         { 

 9             if(array[j] < array[j - 1]) 

10             { 

11                 Swap(array, j, j-1); 

12             } 

13         } 

14     } 

15 }

Shell Sort: Runtim: O(nlog2^n) ~ O(n^1.5).

 1 void ShellSortArray() 

 2 { 

 3     for(int incr=3;incr<0;incr--)//增量递减，以增量3，2，1为例 

 4     { 

 5         for(int L=0;L<(n-1)/incr;L++)//重复分成的每个子列表 

 6         { 

 7            for(int i=L+incr;i<n;i+=incr)//对每个子列表应用插入排序 

 8            { 

 9                 int temp=arr[i]; 

10                 int j=i-incr; 

11                 while(j>=0&&arr[j]>temp) 

12                 { 

13                   arr[j+incr]=arr[j]; 

14                   j-=incr; 

15                 } 

16             arr[j+incr]=temp; 

17             } 

18         } 

19     } 

20 } 

 

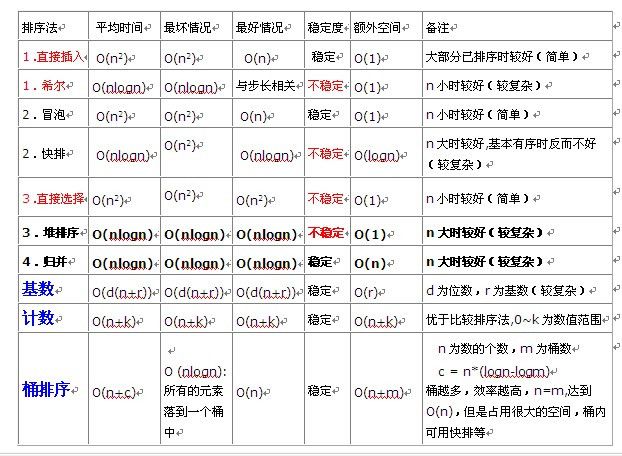
总结：

1.O(n^2)性能分析

平均性能为O(n^2)的有：直接插入排序，选择排序，冒泡排序

在数据规模较小时（9W内），直接插入排序，选择排序差不多。当数据较大时，冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本上是相邻元素进行比较，基本上都是稳定的。

2.O(nlogn)性能分析

平均性能为O(nlogn)的有：快速排序，归并排序，希尔排序，堆排序。其中，快排是最好的， 其次是归并和希尔，堆排序在数据量很大时效果明显。

这四种排序可看作为“先进算法”，其中，快排效率最高，但在待排序列基本有序的情况下，会变成冒泡排序，接近O(n^2).

希尔排序对增量的标准没有较为满意的答案，增量对性能会有影响。

归并排序效率非常不错，在数据规模较大的情况下，比希尔排序和堆排序要好。

多数先进的算法都是因为跳跃式的比较，降低了比较次数，但牺牲了排序的稳定性。

3. 插入排序，冒泡排序，二叉树排序，归并排序都是稳定的

 选择排序，希尔排序，快速排序，堆排序是不稳定的。

四、排序算法选择

1.数据规模较小

  （1）待排序列基本序的情况下，可以选择直接插入排序；

  （2）对稳定性不作要求宜用选择排序，对稳定性有要求宜用插入或冒泡

2.数据规模不是很大

（1）完全可以用内存空间，序列杂乱无序，对稳定性没有要求，快速排序，此时要付出log（N）的额外空间。

 （2）序列本身可能有序，对稳定性有要求，空间允许下，宜用归并排序

3.海量级别的数据，必须按块放在外存上

   （1）对稳定性有求，则可考虑归并排序。

    （2）对稳定性没要求，宜用堆排序

4.序列初始基本有序（正序），宜用直接插入，冒泡，随机快排

外部排序

外部排序指的是大文件的排序，面试的时候，面试官喜欢问，给你一个非常非常大的文件（比如1T），一行一个数（或者一个单词），内存最多只有8G，硬盘足够大，CPU很高级……然后要你给这个文件里面的数据排序。你要怎么办？

这其实就要用到外部排序。就是说要借助外存储器进行多次的内/外存数据的交换，因为内存不足以加载所有的数据，所以只能一部分一部分地加载。

所以外部排序的思想就是：分两个独立的阶段。

首先，可按内存的大小，将外存上含n个记录的文件分成若干长度为 x 的子文件或段，依次读入内存，并利用有效的内部排序方法对它们进行排序，并将排序后得到的有序子文件 重新写入外存，通常称这些有序的子文件为归并段或顺串。然后，对这些归并段进行逐趟归并，使归并段逐渐由小到大，直至得到整个有序文件为止。

因此现在的问题就转化为如何归并两个大文件。这个读者朋友们想一下就明白了。就是把这两个文件按内存的大小，一部分一部分从小到大加载出来并，再写回外存。

Questions:

11.1 Given two sorted arrays, A and B, where A has a large enough buffer at the end to hold B.

Merge a and b, starting from the last element in each!

11.2 Write a method to sort an array of strings so that all the anagrams are next to each other.

Implement comparator for this problem:

 1 public class AnagramComparator implements Comparator<String>{

 2     public String sortChars(String s){

 3         char[] content = s.toCharArray();

 4         Arrays.sort(content);

 5         return new String(content);

 6     }

 7     public int compare(String s1, String s2){

 8         return sortChars(s1).compareTo(sortChars(s2));

 9     }

10 }

 1 public void sort(String[] array){

 2     Hashtable<String, LinkedList<String>> hash = new Hashtable<String, LinkedList<String>>();

 3     for(String s : array){

 4         String key = sortChars(s);

 5         if(!hash.containsKey(key)) hash.put(key, new LinkedList<String>());

 6         LinkedList<String> anagrams = hash.get(key);

 7         anagrams.push(s);

 8     }

 9     int index = 0;

10     for(String key : hash.keySet()){

11         LinkedList<String> list = hash.get(key);

12         for(String t : list){

13             array[index] = t;

14             index ++;

15         }

16     }

17 }

The algorithm above is a modification of bucket sort.

11.3 Given a sorted array of n integers that has been rotated an unknown number of times, write code to find an element in the array. the array is sorted in increasing order at begining.

 If we look a bit deeper, we can see that one half of the array must be ordered normally(in increasing order).We can therefore look at the normally ordered half to determine whether we should search the left or right half.

 

 1 public int search(int[] array, int left, int right, int x){

 2     int mid = (left + right) / 2;

 3     if(x == array[mid]) return mid;

 4     if(left < right) return -1;

 5     //either the left or right half must be normally ordered. find out which side is normally ordered, and then use the normally ordered half to figure out which side to search to find x.

 6     if(array[left] < array[mid]){//left half normally ordered

 7         if(x >= array[left] && x <= array[mid]) return search(array, left, mid - 1, x);

 8         else return search(array, mid + 1, right, x);

 9     }else if(array[mid] < array[left]){//right is normally ordered

10         if(x >= array[mid] && x <= array[right]) return search(array, mid + 1, right, x);

11         else return search(array, left, mid - 1, x);

12     }else if(array[left] == array[mid]){// left half is all repeats

13         if(array[mid] != array[right]) return search(array, mid + 1, right, x);

14         else{// else we have to search both halves

15             int result = search(array, left, mid - 1, x);

16             if(result == -1) return search(array, mid + 1, right, x);

17             else return result;

18         }

19     }

20     return -1;

21 }

 

11.4 Imagine you hace a 20GB file with one string per line. Explain how you would sort the file.

When an interviewer gives a size limit, it should tell you that they don't want you to bring all the data into memory.

So we should only bring part of the data into memory.

We'll divide the file into chunks which are xMB each, where x is the amout of memory we have available. Each chunk is sorted separately and then saved back to the file system.

Once all the chunks are sorted, we then merge the chunks, one by one. At the end, we have a fully sorted file.

 11.8 Imagine you are reading in a stream of integers. Periodically, you wish to be able to look up the rank of a number x(the number of values less than or equal to x). Implement the data structures and algorithms to support these operations.

 1 public class Question{

 2     private static RankNode root = null;

 3     public static void track(int number){

 4         if(root == null) root = new RankNode(number);

 5         else root.insert(number);

 6     }

 7     public static int getRankOfNumber(int number){

 8         return root.getRank(number);

 9     }

10     ...

11 }

12 public class RankNode{

13     public int left_size = 0;

14     public RankNode left, right;

15     public int data = 0;

16     public RankNode(int d){

17         data = d;

18     }

19     public void insert(int d){

20         if(d <= data){

21             if(left != null) left.insert(d);

22             else left = new RankNode(d);

23             left_size ++;

24         }else{

25             if(right != null) right.insert(d);

26             else right = new RankNode(d);

27         }

28     }

29     public int getRank(int d){

30         if(d == data) return left_size;

31         else if(d < data){

32             if(left == null) return -1;

33             else return left.getRank(d);

34         }else{

35             int right_rank = right == null ? -1 : right.getRank(d);

36             if(right_rank == -1) return -1;

37             else return left_size + 1 + right_rank;

38         }

39     }

40 }