【学习笔记】灰色预测 GM(1,1) 模型 —— Matlab

---

前言

通过模型算法，熟练对Matlab的应用。
学习视频链接：
https://www.bilibili.com/video/BV1EK41187QF?p=48&vd_source=67471d3a1b4f517b7a7964093e62f7e6

一、灰色预测模型

灰色系统理论在另一篇博客中已经阐述过了，此处不作赘述。

参考链接：【学习笔记】Matlab和python双语言的学习(灰色关联分析法）

灰色预测

• 所谓灰色预测，就是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。

适用情况

1. 数据是以年份度量的非负数据(如果是月份或者季度数据一般要用时间序列模型)，比如定时求量的题目，即已知一些年份数据，预测下一年的数据，常见有GDP、人口数量、耕地面积、粮食产量等；或者定量求时，已知一些年份数据和某灾变的阈值，预测下次灾变时间。
2. 数据能经过准指数规律的检验(除了前两期外，后面至少90%的期数的光滑比要低于0.5)。
3. 数据的期数较短且和其他数据之间的关联性不强(小于等于10，也不能太短了，比如只有3期数据)，要是数据期数较长，一般用传统的时间序列模型比较合适。

GM (1,1)模型

• $GM:Greymodel$ 灰色模型，
• $(1,1):$ 只含有一个变量的一阶微分方程模型
• 如何用 $GM(1,1)$ 进行灰色预测？
  • 根据原始的离散非负数据列，通过累加等方式削弱随机性、获得有规律的离散数据列
  • 建立相应的微分方程模型，得到离散点处的解
  • 再通过累减求得的原始数据的估计值，从而对原始数据预测

二、示例

• 长江在 1995-2004 年废水排放总量如下，如果不采取保护措施，请对今后水质污染发展趋势做出预测。
  

指数规律检验(原始数据级比检验)

级比检验的定义

• 为了确定原始数据是否可使用灰色预测模型，需要对原始数据进行级比检验
• 要使用灰色预测数据首先应具有准指数规律：
  累加 $r$ 次的序列为：$x^{(r)}=\left(x^{(r)}(1),x^{(r)}(2),...,x^{(r)}(n)\right)$，定义级比 $\sigma (k)=\frac{x^{(r)}(k)}{x^{(r)}(k-1)},k=2,3,...,n$
  对于 $\forall k,\sigma (k)\in [a,b]$，且区间长度 $\delta =b-a<0.5$，则称累加 $r$ 次后的序列具有准指数规律

GM(1,1) 模型的级比检验

• 对于 $GM(1,1)$ 模型中，我们只需要判断累加一次后的序列 $x^{(1)}=\left(x^{(1)}(1),x^{(1)}(2),\dots ,x^{(1)}(n)\right)$ 是否具有准指数规律
• 根据上述公式：序 列 $x^{(1)}$ 的级比 $\sigma (k)=\frac{x^{(1)}(k)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)+x^{(1)}(k-1)}{x^{(1)}(k-1)}=\frac{x^{(0)}(k)}{x^{(1)}(k-1)}+1$
• 定义 $\rho (k)=\frac{x^{(0)}(k)}{x^{(1)}(k-1)}$ 为原始序列 $x^{(0)}$ 的光滑比，注意到 $\rho (k)=\frac{x^{(0)}(k)}{x^{(0)}(1)+x^{(0)}(2)+\cdots +x^{(0)}(k-1)}$，假设$x^{(0)}$ 为非负序列(生活中常见的时间序列几乎都满足非负性)，那么随着 $k$ 增加，最终 $\rho (k)$ 会逐渐接近0，因此要使得具有 $x^{(1)}$ 具有准指数规律，即 $\forall k$，区间长度 $\delta <0.5$，只需要保证 $\rho (k)\in (0,0.5)$ 即可，此时序列 $x^{(1)}$ 的级比 $\sigma (k)\in (1,1.5)$。
• 实际建模中，我们要计算出 $\rho (k)\in (0,0.5)$ 的占比，占比越高越好(一般$\rho (2)$和$\rho (3)$可能不符合，重点关注后面的数据)

模型求解

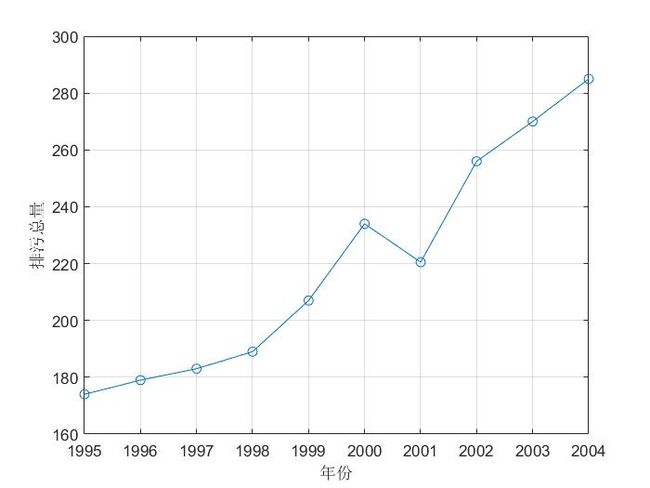
• 观察发现，没有明显规律，数据也比较少， 而且是以年份度量的，可以考虑用灰色预测
• 那看不出规律怎么办，可以制造规律：

设$x^{(0)}=(x^{(0)}(1),x^{(0)}(2),...,x^{(0)}(n))$是最初的非负数据列，我们可以对其累加，得到新的数据列$x^{(1)}$
$$x^{(1)}=\left(x^{(1)}(1),x^{(1)}(2),\dots ,x^{(1)}(n)\right)$$
其中：$x^{(1)}(m)={\sum }_{\mathrm{i}=1}^{\mathrm{m}}{x}^{(0)}(i),m=1,2,...,n$

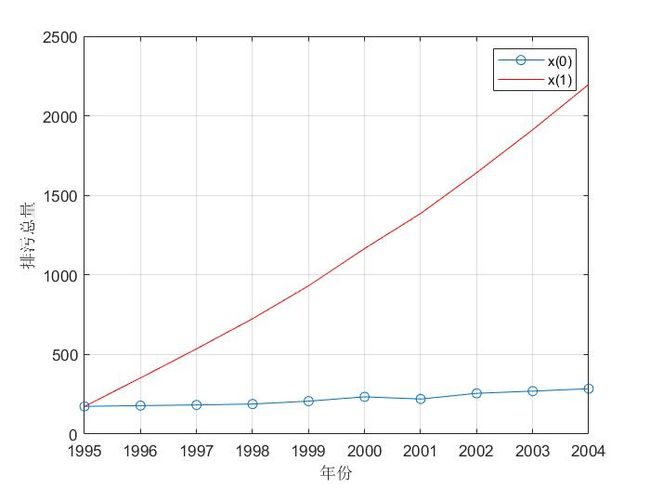
• 观察可知，新序列 $x^{(1)}$ 曲线像一个指数曲线(直线)
• 我们可以用指数曲线的表达式来逼近序列 $x^{(1)}$，相应可以构建一阶常微分方程来求解拟合指数曲线的函数表达式
• 一阶常微分方程
  $$\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}=u$$
  要求出 $x^{(1)}$ 的表达式，就需要解出常微分方程，所以要先知道参数 $a$ 和 $u$。

求解微分方程

• 一阶常微分方程
  $$\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}=u$$
• 已知，我们的数据是离散的，所以 $\frac{d{x}^{(1)}}{dt}$ 等同于 $$\frac{\Delta x^{(1)}}{\Delta t}=\frac{\Delta x^{(1)}}{t-(t-1)}=\Delta x^{(1)}=x^{(1)}(t)-x^{(1)}(t-1)=x^{(0)}(t)$$
  则微分方程变为 $x^{(0)}(t)+a{x}^{(1)}(t)=u$
• 上式为常见的一元线性方程，为了消除数据随机性，定义$z^{(1)}=(z^{(1)}(1),z^{(1)}(2),...,z^{(1)}(n))$
  其中：$z^{(1)}(m)=\delta x^{(1)}(m)+(1-\delta )x^{(1)}(m-1),m=2,3,...,n$ 且$\delta =0.5$，即为前后时刻的均值
• 则微分方程改为 $x^{(0)}(t)=-a{z}^{(1)}(t)+u$
• 我们已知$x^{(0)}(t),z^{(1)}(t)$的数据，结合线性回归的知识，可利用线性回归或者用最小二乘法求解参数
• 把 $\hat{a}$ 和 $\hat{u}$ 代入微分方程 $\frac{d{x}^{(1)}}{dt}+a{x}^{(1)}=u$，并求解可得
  ${\hat{x}}^{(1)}(m+1)=\left[x^{(0)}(1)-\frac{\hat{u}}{\hat{a}}\right]e^{-\hat{a}m}+\frac{\hat{u}}{\hat{a}},m=1,2,...,n-1$
• 由于 $x^{(1)}(m)={\sum }_{\mathrm{i}=1}^{\mathrm{m}}{x}^{(0)}(i),m=1,2,...,n$，所以我们可以得到：
  $${\hat{x}}^{(0)}(m+1)={\hat{x}}^{(1)}(m+1)-{\hat{x}}^{(1)}(m)=\left(1-e^{\hat{a}}\right)\left[x^{(0)}(1)-\frac{\hat{u}}{\hat{a}}\right]e^{-\hat{a}m},m=1,2,...,n-1$$
• 当 $m$ 取 0,1,…,9 时，得到的 ${\hat{x}}^{(0)}$ 为拟合值，大于 9 时，得到的为预测值

模型评价(检验模型对原始数据的拟合程度)

残差检验

• 绝对残差：$ϵ(k)=x^{(0)}(k)-{\hat{x}}^{(0)}(k),k=2,3,...,n$
• 相 对 残 差：${ϵ}_r(k)=\frac{|x^{(0)}(k)-{\hat{x}}^{(0)}(k)|}{x^{(0)}(k)}\times 100\%,k=2,3,...,n$
• 平均相对残差：${\overline{ϵ}}_r=\frac{1}{n-1}{\sum }_{k=2}^n|{ϵ}_r(k)|$
  • 如果${\overline{ϵ}}_r<20\%$，则认为 $GM(1,1)$ 对原数据的拟合达到一般要求
  • 如果${\overline{ϵ}}_r<10\%$，则认为 $GM(1,1)$ 对原数据的拟合效果非常不错

级比偏差检验

首先计算原始数据级比 $\sigma (k)=\frac{x^{(0)}(k)}{x^{(0)}(k-1)}\left(k=2,3,\dots ,n\right)$

再根据预测发展系数 $(-\hat{a})$ 计算级比偏差和平均级比偏差
η ( k ) = ∣ 1 − 1 − 0.5 a ^ 1 + 0.5 a ^ 1 σ ( k ) ∣ ,   η ‾ = ∑ k = 2 n η ( k ) / ( n − 1 ) \eta(k)=\left|1-\frac{1-0.5\hat{a}}{1+0.5\hat{a}}\frac{1}{\sigma(k)}\right|,\:\overline{\eta}=\sum_{k=2}^{n}\eta(k)/(n-1) η(k)= ​1−1+0.5a^1−0.5a^​σ(k)1​ ​,η​=k=2∑n​η(k)/(n−1)
如果 $\bar{\eta }<0.2$，则认为模型对原数据拟合达到一般要求；$\bar{\eta }<0.1$，则认为模型对原数据拟合效果非常不错

三、代码实现----Matlab

级比检验代码

clear;clc
year =[1995:1:2004]';  % 横坐标表示年份，写成列向量的形式
x0 = [174,179,183,189,207,234,220.5,256,270,285]';  %原始数据序列，写成列向量的形式

n = size(x0,1);
x1 = zeros(n,1);
for i = 1:n
    x1(i) = sum(x0(1:i,1));
end

% 级比检验
rho = zeros(n,1);
for i = 2:n
    rho(i) = x0(i) / x1(i-1);
end
figure(2)
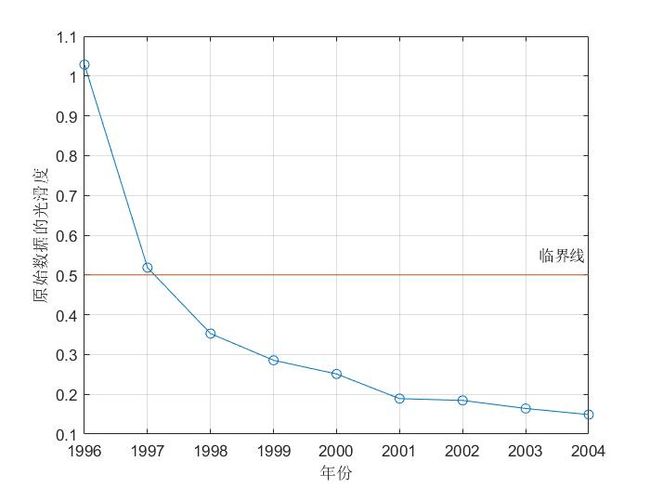
plot(year(2:n,1),rho(2:n,1),'o-',[year(2),year(n)],[0.5,0.5],'-'); grid on;
text(year(end-1)+0.2,0.55,'临界线')   % 在坐标(year(end-1)+0.2,0.55)上添加文本
set(gca,'xtick',year(2:1:end))  % 设置x轴横坐标的间隔为1
xlabel('年份');  ylabel('原始数据的光滑度');  % 给坐标轴加上标签
% 指标1：光滑比小于0.5的数据占比
num1 = sum(rho<0.5)/(n-1)
% 指标2：除去前两个时期外，光滑比小于0.5的数据占比
num2 = sum(rho(3:end)<0.5)/(n-3)

运行结果：

参考标准：指标1一般要大于60%, 指标2要大于90%，所以通过了级比检验。

模型求解代码

function [result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num)
    n = size(x0,1);
    x1 = cumsum(x0);
    z1 = 0.5 * x1(2:end) + 0.5 * x1(1:n-1,1)
    y = x0;
    x = z1;
    [b,bint,r,rint,stats]=regress(y, x);  % 调用一元线性回归函数求解a和u
    a = -b(1);
    u = b(2);
    x0_hat = zeros(n,1);
    x0_hat(1) = x0(1);
    for m = 1: n-1
        x0_hat(m+1) = (1-exp(a))*(x0(1)-u/a)*exp(-a*m);
    end
    result = zeros(predict_num,1);  % 初始化用来保存预测值的向量
    for i = 1: predict_num
        result(i) = (1-exp(a))*(x0(1)-u/a)*exp(-a*(n+i-1)); % 带入公式直接计算
    end
    % 计算绝对残差和相对残差
    absolute_residuals = x0(2:end) - x0_hat(2:end);   % 从第二项开始计算绝对残差，因为第一项是相同的
    relative_residuals = abs(absolute_residuals) ./ x0(2:end);  % 计算相对残差
    % 计算级比和级比偏差
    class_ratio = x0(2:end) ./ x0(1:end-1) ;  % 计算级比
    eta = abs(1-(1-0.5*a)/(1+0.5*a)*(1./class_ratio));  % 计算级比偏差
end

% 函数作用：使用传统的GM(1,1)模型对数据进行预测
%     x0：要预测的原始数据
%     predict_num： 向后预测的期数

% 输出变量
%     result：预测值
%     x0_hat：对原始数据的拟合值
%     relative_residuals： 对模型进行评价时计算得到的相对残差
%     eta： 对模型进行评价时计算得到的级比偏差

调用模型求解代码进行预测

if num1 > 0.6 && num2 > 0.9
    if n > 7    % 将数据分为训练组和试验组(根据原数据量大小n来取，n小于7则取最后两年为试验组，n大于7则取最后三年为试验组)
        test_num = 3;
    else
        test_num = 2;
    end
    train_x0 = x0(1:end-test_num);  % 训练数据
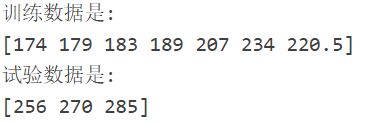
    disp('训练数据是: ')
    disp(mat2str(train_x0'))  % mat2str可以将矩阵或者向量转换为字符串显示
    test_x0 =  x0(end-test_num+1:end); % 试验数据
    disp('试验数据是: ')
    disp(mat2str(test_x0'))
    
    % 使用GM（1，1）模型对训练数据进行训练
    disp('GM(1,1)模型预测')
    result1 = gm11(train_x0, test_num); %预测后test_num期的结果
    % 绘制对试验数据进行预测的图形
    test_year = year(end-test_num+1:end);  % 试验组对应的年份
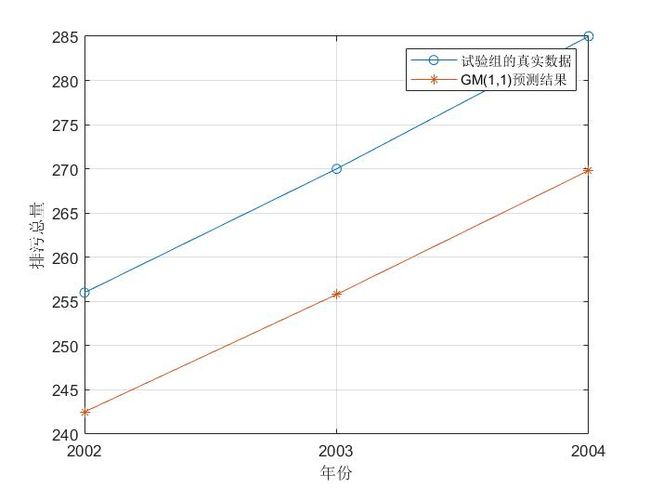
    figure(3)
    plot(test_year,test_x0,'o-',test_year,result1,'*-'); grid on;
    set(gca,'xtick',year(end-test_num+1): 1 :year(end))
    legend('试验组的真实数据','GM(1,1)预测结果') 
    xlabel('年份');  ylabel('排污总量');  % 给坐标轴加上标签
 
    predict_num = input('请输入你要往后面预测的期数： ');
    % 计算使用传统GM模型的结果
    [result, x0_hat, relative_residuals, eta] = gm11(x0, predict_num);
    
    %% 绘制相对残差和级比偏差的图形
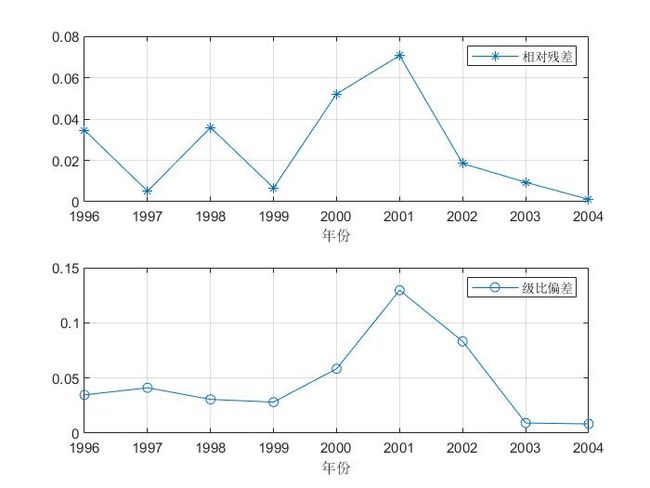
    figure(4)
    subplot(2,1,1)  % 绘制子图（将图分块）
    plot(year(2:end), relative_residuals,'*-'); grid on;   % 原数据中的各时期和相对残差
    legend('相对残差'); xlabel('年份');
    set(gca,'xtick',year(2:1:end))  % 设置x轴横坐标的间隔为1
    subplot(2,1,2)
    plot(year(2:end), eta,'o-'); grid on;   % 原数据中的各时期和级比偏差
    legend('级比偏差'); xlabel('年份');
    set(gca,'xtick',year(2:1:end))
    
    %% 残差检验
    average_relative_residuals = mean(relative_residuals);  % 计算平均相对残差 mean函数用来均值
    disp(strcat('平均相对残差为',num2str(average_relative_residuals)))
    
    %% 级比偏差检验
    average_eta = mean(eta);   % 计算平均级比偏差
    disp(strcat('平均级比偏差为',num2str(average_eta)))
    
    %% 绘制最终的预测效果图
    figure(5) 
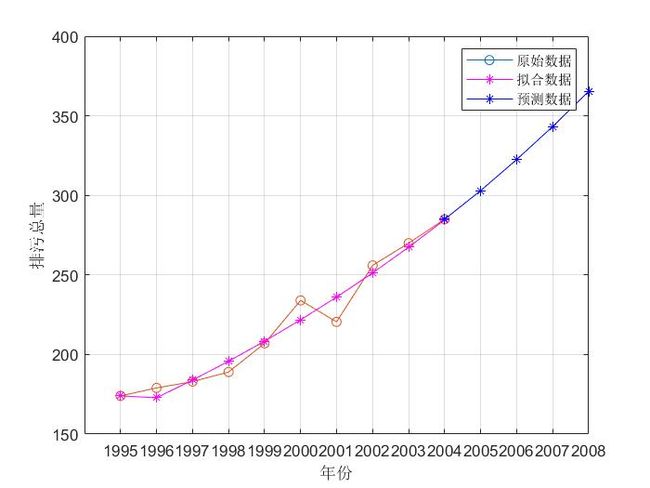
    plot(year,x0,'-o',  year,x0_hat,'-*m',  year(end)+1:year(end)+predict_num,result,'-*b' );   grid on;
    hold on;
    plot([year(end),year(end)+1],[x0(end),result(1)],'-*b')
    legend('原始数据','拟合数据','预测数据')  
    set(gca,'xtick',[year(1):1:year(end)+predict_num])  
    xlabel('年份');  ylabel('排污总量');  
end

运行结果：

可以看出：平均相对残差为：0.025999 ＜ 10 %
级比偏差为 0.047041 ＜ 0.1 拟合效果非常不错