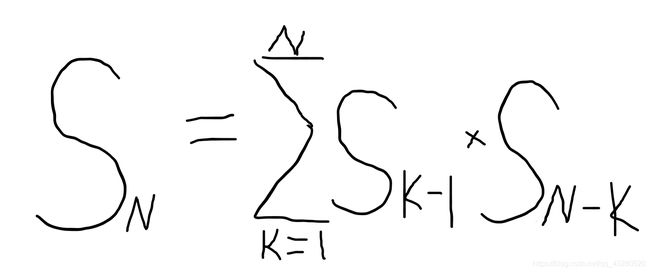贪心+基本数据结构——栈

今日学习情况：

昨天跟bf吵架，导致今天看小说没欲望，听音乐触景伤情，加上一不干正事就会想起她来以至于一直，所以学习时间居然莫名边长了？？虽然不知道学习效率怎么样，但我赶脚还行，和平时没有什么区别的样子。

今天有学习剩下的一点点贪心，贪心一般来说是最简单的算法了，但是这里题目我依然有很多不会！！还有数据结构里面栈的用法，但是栈怎么写我忘记了，大概是用一个数组和一个int类型的名为top的数值作为栈顶标记，每放入一个数值，top+1，要执行出战操作，就top-1，假装数字已经不存在了。

这本书重点讲了他们的用法，对我这种基础不好的人十分的不友善！好就好在以前的ppt我没删哈哈哈哈哈哈

练习赛：虽然早知道第二个题一个数一个数换会超时，可是我不知道到底该怎么优化，就算是字符串整体也只是某一行可以改变而已……哎，不想写题了，看也看不懂，想也想不出来，即使想出来也超时。

他们说暴力做，但是有点改动。

明天补题，我想补一天！！！！啊！！！！！

贪心：

现在大部分同学都可以看到一个题，判断出它是否可以使用贪心，但是仍然有判断错误的时候，如何检验呢？

1.微扰（领项交换）：证明在任意局部最优的微小改变会影响整体结果的最优。

2.范围缩放：对局部最优策略的范围改变都不会造成整体的结果变差。

3.决策包容性：局部最优解策略所包含的可能性包含其他所有策略提供的可能性。

4.反证法。

5.数学归纳法。

贪心就是要多看例题，多看例题就好了，这里就不一一整理例题了（我第一次知道贪心算法原来也这么难！！）。

基本数据结构之栈

为什么要学数据结构？

以前总感觉数据结构学起来好像没有什么用，但是今天读了一些博客才意识到，原来数据结构就是所有数据的基础，只有了解了他们，我们才能更好的管理数据，更重要的是，学习一种将现实问题转换为计算机语言的思想（栈的数据结构不就是相当于将那个栈的入栈出栈的过程，变成一个计算机语言表示出来的过程吗？）

栈的数据结构（最简单的一版）

网上写的都好难，不是结构体就是指针……写代码的时候完全不可能用上好嘛？！所以这个最简单的，就是只是用数组和类指针模拟的栈（只有进出两个操作）。

栈是一种先进后出的线性数据结构，只有一端能够进出元素，我们称可以进出元素的一端为栈顶，另一端为栈底，在添加或者删除元素的时候，我们只能将其插入栈顶（进栈），或者把栈顶元素从栈中取出（出栈）。

栈是实现深度优先搜索的基本结构

代码：

#define n 100
void push(int s[],int top,int x)  //入栈
{
   if (top==n) cout<<"overflow"<

栈基本例题：

（1）Push，Pop，Getmin

题目大意：实现一个栈，支持入栈、出栈、查找最小值的操作（最大值类比）

思路：设置两个栈，一个栈存放数据，实现基础的入栈、出栈操作，但是基础的栈却不能查询栈中的最小值顺便更新最小值。

想法1:用一个小根堆，想要最小值输出堆顶即可。但是维护一个栈+小根堆，空间复杂度太高，pass。

想法2：用一个数据存储最小值，但是一旦出栈，最小值就找不到了，所以pass。

想法3：用一个栈来保存每个状态的最小值，入栈的化，栈值跟前一个状态的最小值比较，出栈就出当前状态最小值，然后就可以直接得到出栈后状态的最小值了——栈顶。

（2）Editor HDOJ4699（内附dalao代码）

题目大意：维护一个整数序列的编译器，有很多操作，比如增加一个数字，光标右移、删除数字、光标左移、光标右移、求光标位置之前某个位置k的最大前缀和。

思路：始终在序列中间进行修改，光标不可能只在最左边或者最右边，如此，我们想到了上一章维护中位数时的对顶堆，每次小根堆的堆顶就是中位数，这个题目也是一直求中间的某个值。

所以我们想到“对顶栈”这样的结构，栈顶就是光标存在的位置，A栈即从序列开始到光标位置，B栈存储从光标位置到末端。

对于I x操作：

①把x插入栈A。

②更新sum[pa]=sum[pa-1]+a[pa]；（pa为栈顶下标，sum[pa]是到pa段的前缀和）

③更新f[pa]=max(f[pa-1],sum[pa])；（f[pa]为前缀和最大值，这个式子为当前位置最大值=前一个状态的最大值与这个状态的前缀和相比较，看看哪个更大）。

对于删除光标前一个数的操作：A的栈顶出栈即可，光标位置改变了，所以此时求前缀和，求出来的就是pa位置的前缀和最大值（已经被存储起来了，就是f[pa]）

对于光标左移的操作：弹出A栈顶，放入B栈。

对于光标右移：

①弹出B的栈顶，插入A中。

②更新sum[pa]=sum[pa-1]+a[pa]；

③更新f[pa]=max(f[pa-1],sum[pa])；

（3）进出栈序列问题

若进栈顺序为1~n，那么可能的出栈顺序有多少种？

方法一：搜索（枚举/递归）o(2^n)

每个状态两个路径：下一个数进栈、当前数出栈

代码：

int stack(int n,int m)//n是准备入栈的个数，m是在栈中的个数
{
    if(n==0) return 1;//如果没有可以入栈的数了，就是达到了结尾，此时方法只有一条
    if(m==0) return (n-1,1);//没有数在栈里面，只能进行入栈操作
    else
        return stack(n-1,m+1)+stack(n,m-1);//入栈路径+出栈路径
}

方法2：递推 o(n^2)

考虑1这个数在出栈序列的位置，若1排在第k位，那么整个序列进出栈的过程为：

1.整数1入栈

2.整数2~k这k+1个数进栈并且出栈（以某种顺序）。

3.整数1出栈（1排在第k位了）

4.整数k+1~n这n-k个数按某种顺序进出栈。

于是整个问题被划分为①前k-1个数进出栈②n-k个数进出栈的问题，而每个子问题又能继续划分下去。得到递推公式：

方法三：动态规划 o(n^2)

对于任意时刻，我们只关心有多少个数尚未入栈，有多少个数在栈中，所以我们可以用f[i][j]来表示有i个数尚未入栈，有j个数在栈里，已经有n-i-j个数出栈，它的数值就是此时的方案总数。

最终状态：f[0][0]=1；（所有数都已经入栈且出栈，方案数只有一个。

需要求起始状态的方案数：f[n][0]。

对于每一步，两种决策依然是某个数进栈、某个数出栈。得动态规划状态方程：

f[i][j]=f[i-1][j+1]+f[i][j-1];

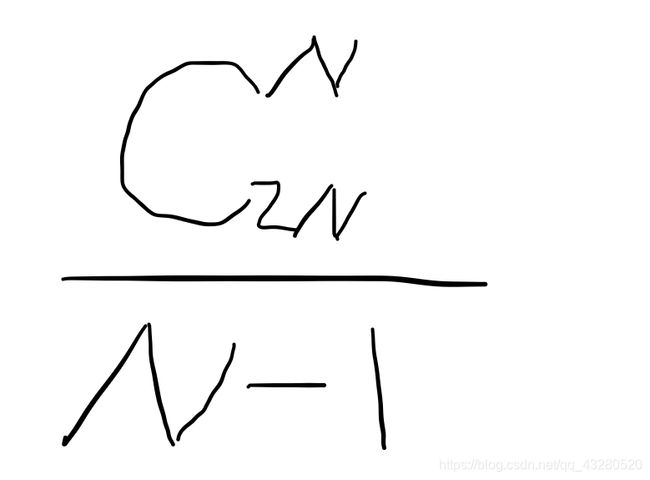
方法四：数学

等于求第n项的Ctalan数，即