数据结构之并查集
找往期文章包括但不限于本期文章中不懂的知识点：
个人主页：我要学编程(ಥ_ಥ)-CSDN博客
所属专栏：数据结构（Java版）
并查集相关概念
并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题（即所谓的并、查）。比如说，我们可以用并查集来判断这两个人是否是亲戚（有没有最近公共祖先）或者两个人是否属于一个阵营等。
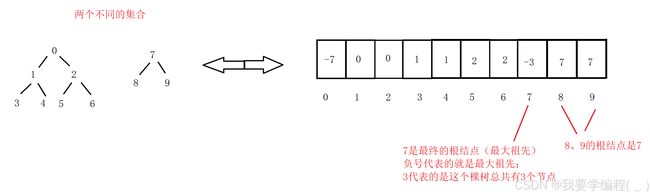
虽然并查集是一种树形结构，但是其底层的实现和堆一样是一个数组。这个数组的大小就代表了我们要处理的集合大小，而这个数组下标对应的值就是这个下标的根结点。如下所示：
通过上述图片我们可以知道一下几个结论：
1、查找元素属于哪个集合沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)；
2、查看两个元素是否属于同一个集合沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在；
3、将两个集合归并成一个集合，即将一个集合的根结点对应的值改为另一个集合的根结点即可；
在改动的时候要注意：
(1)：另一个集合被改的下标为未被改的集合的根结点
(2)：未被改的集合的根结点的值要发生改变：加上另一个集合根结点的值。
4、集合的个数：遍历数组，数组中元素为负数的个数即为集合的个数。
模拟实现并查集
public class UnionFindSet {
public int[] elem;
// 将数组初始化为-1，证明每个元素刚开始都是一个独立的集合
public UnionFindSet() {
elem = new int[10];
Arrays.fill(elem, -1);
}
public UnionFindSet(int n) {
elem = new int[n];
Arrays.fill(elem, -1);
}
// 找到val对应的根结点
public int findRoot(int val) {
// 注意val是数组的下标
// 得判断下标的合法性
if (val < 0) {
throw new IndexOutOfBoundsException("数据下标不合法");
}
// 只有当数组下标对应的值为负数时，才算找到了根节点
while (elem[val] >= 0) {
val = elem[val];
}
return val;
}
// 合并两个元素
public void union(int val1, int val2){
if (val1 < 0 || val2 < 0) {
throw new IndexOutOfBoundsException("数据下标不合法");
}
// 先找到对应的根结点
int index1 = findRoot(val1);
int index2 = findRoot(val2);
// 如果根结点一致，就无需合并了
if (index1 == index2) {
return;
}
// 这种合并方法会导致两棵树的高低不均匀
/* elem[index1] += elem[index2];
elem[index2] = index1;*/
// 开始合并：看哪个树高，就把哪个树作为母树
if (index1 < index2) {
// index1树高
elem[index1] += elem[index2];
elem[index2] = index1;
} else {
// index2树高
elem[index2] += elem[index1];
elem[index1] = index2;
}
}
// 判断两个元素是否在同一个集合中
public boolean isSameSet(int val1, int val2) {
// 看看找到的根结点是否一样
int index1 = findRoot(val1);
int index2 = findRoot(val2);
if (index1 == index2) {
return true;
}
return false;
}
// 求数组中集合的个数
public int getCountSet() {
int count = 0;
for (int x : elem) {
// 如果元素下标对应的值为负树，则说明是一个集合
if (x < 0) {
count++;
}
}
return count;
}
// 打印集合中的全部元素
public void printElem() {
for (int i = 0; i < elem.length; i++) {
System.out.print(i+" ");
}
System.out.println();
}
}
总体实现还是比较简单的。
并查集的应用
547.省份数量
题目：
有
n个城市，其中一些彼此相连，另一些没有相连。如果城市a与城市b直接相连，且城市b与城市c直接相连，那么城市a与城市c间接相连。省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给你一个
n x n的矩阵isConnected，其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连，而isConnected[i][j] = 0表示二者不直接相连。返回矩阵中 省份 的数量。
示例 1：
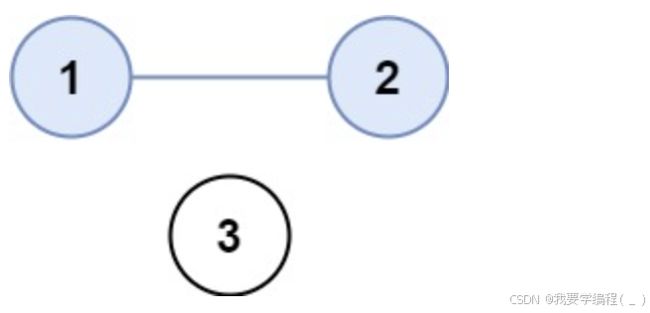输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出：2示例 2：
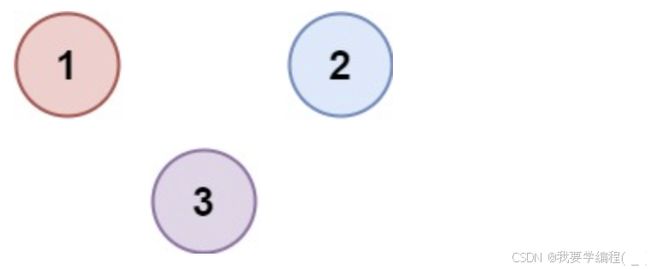输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出：3提示：
1 <= n <= 200n == isConnected.lengthn == isConnected[i].lengthisConnected[i][j]为1或0isConnected[i][i] == 1isConnected[i][j] == isConnected[j][i]
思路：通过阅读题目可知：相邻的城市被称为一组省份，而我们要做的就是把省份的数量统计出来。利用并查集的思想就是：把相邻的城市合并成一个集合，然后再求集合的数量。相邻的城市就是 isConnected[i][j] == 1，因此只需要遍历数组，如果相邻，就合并；最后再看集合的数量。
代码实现：
class Solution {
public int findCircleNum(int[][] isConnected) {
// 因为这个数组并不是按照我们的要求来创建的，因此得发生改变
// 重新创建一个数组
// ufs底层的数组的长度就是城市的个数（因为最终合并的还是城市）
UnionFindSet ufs = new UnionFindSet(isConnected.length);
// 遍历数组将相邻的城市合并成一组省份
for (int i = 0; i < isConnected.length; i++) {
// 根据 提示可知：isConnected[i][j] == isConnected[j][i]
// 即 j = i+1，也是可以的(类似去重了)
for (int j = 0; j < isConnected[i].length; j++) {
if (isConnected[i][j] == 1) {
ufs.union(i, j);
}
}
}
return ufs.getCountSet();
}
}
class UnionFindSet {
public int[] elem;
// 将数组初始化为1，证明每个元素刚开始都是一个独立的集合
public UnionFindSet() {
elem = new int[10];
Arrays.fill(elem, -1);
}
public UnionFindSet(int n) {
elem = new int[n];
Arrays.fill(elem, -1);
}
// 找到val对应的根结点
public int findRoot(int val) {
// 注意val是数组的下标
// 得判断下标的合法性
if (val < 0) {
throw new IndexOutOfBoundsException("数据下标不合法");
}
while (elem[val] >= 0) {
val = elem[val];
}
return val;
}
// 合并两个元素
public void union(int val1, int val2){
if (val1 < 0 || val2 < 0) {
throw new IndexOutOfBoundsException("数据下标不合法");
}
// 先找到对应的根结点
int index1 = findRoot(val1);
int index2 = findRoot(val2);
// 如果根结点一致，就无需合并了
if (index1 == index2) {
return;
}
/* elem[index1] += elem[index2];
elem[index2] = index1;*/
// 开始合并：看哪个树高，就把哪个树作为母树
if (index1 < index2) {
// index1树高
elem[index1] += elem[index2];
elem[index2] = index1;
} else {
// index2树高
elem[index2] += elem[index1];
elem[index1] = index2;
}
}
// 判断两个元素是否在同一个集合中
public boolean isSameSet(int val1, int val2) {
// 看看找到的根结点是否一样
int index1 = findRoot(val1);
int index2 = findRoot(val2);
if (index1 == index2) {
return true;
}
return false;
}
// 求数组中集合的个数
public int getCountSet() {
int count = 0;
for (int x : elem) {
// 如果元素下标对应的值为负树，则说明是一个集合
if (x < 0) {
count++;
}
}
return count;
}
// 打印集合中的全部元素
public void printElem() {
for (int i = 0; i < elem.length; i++) {
System.out.print(i+" ");
}
System.out.println();
}
}上面是其中一种处理方式：创建一个新的同等大小的数组，并实现一个并查集；另外一种方式是：直接创建一个数组，实现部分方法：合并、求根、求集合个数。
代码实现：
class Solution {
public int findCircleNum(int[][] isConnected) {
// 创建一个新的数组
int[] nums = new int[isConnected.length];
Arrays.fill(nums, -1);
for (int i = 0; i < isConnected.length; i++) {
for (int j = 0; j < isConnected[i].length; j++) {
if (isConnected[i][j] == 1) {
union(nums, i, j);
}
}
}
return getCountSet(nums);
}
private int getCountSet(int[] nums) {
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] < 0) {
count++;
}
}
return count;
}
private void union(int[] nums, int i, int j) {
// 合并两个集合
int index1 = findRoot(nums, i);
int index2 = findRoot(nums, j);
// 同一个集合就不做处理
if (index1 == index2) {
return;
}
// 根据母树的高度来处理
if (index1 < index2) {
nums[index1] += nums[index2];
nums[index2] = index1;
} else {
nums[index2] += nums[index1];
nums[index1] = index2;
}
}
private int findRoot(int[] nums, int i) {
// 题目给的数据都是合法的
while (nums[i] >= 0) {
i = nums[i];
}
return i;
}
}990.等式方程的可满足性
题目：
给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程
equations[i]的长度为4，并采用两种不同的形式之一："a==b"或"a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回
true，否则返回false。示例 1：
输入：["a==b","b!=a"] 输出：false 解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。示例 2：
输入：["b==a","a==b"] 输出：true 解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。示例 3：
输入：["a==b","b==c","a==c"] 输出：true示例 4：
输入：["a==b","b!=c","c==a"] 输出：false示例 5：
输入：["c==c","b==d","x!=z"] 输出：true提示：
1 <= equations.length <= 500equations[i].length == 4equations[i][0]和equations[i][3]是小写字母equations[i][1]要么是'='，要么是'!'equations[i][2]是'='
思路：其实就是遍历数组，将等价的方程字母放置一个集合。第二次遍历的时候，如果出现了不在这个集合中的元素，那么就肯定不满足；如果遍历完成之后，没有返回，那么就满足了。这里其实运用的是并查集的思想。
代码实现：
错误代码示例：
class Solution {
// 错误解法：
public boolean equationsPossible(String[] equations) {
Set set = new TreeSet<>();
for (int i = 0; i < equations.length; i++) {
char ch1 = equations[i].charAt(0);
char ch2 = equations[i].charAt(3);
// 属于同一个集合就入
if ((equations[i].charAt(1) == '=') && (ch1 != ch2) ) {
set.add(ch1);
set.add(ch2);
}
}
for (int i = 0; i < equations.length; i++) {
char ch1 = equations[i].charAt(0);
char ch2 = equations[i].charAt(3);
// ！下并存在集合中或者本身相同，就返回false
if (equations[i].charAt(1) == '!') {
if ((set.contains(ch1) && set.contains(ch2)) || (ch1 == ch2) ) {
return false;
}
}
}
return true;
}
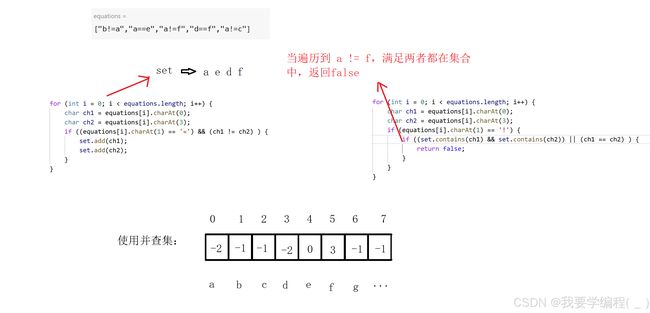
} 上面的代码可以跑过大部分的情况，但是还有一种情况是不行的。如下图所示：
因此，正确的解法是用并查集。
class Solution {
public boolean equationsPossible(String[] equations) {
// 普通的集合行不通，只能用并查集解决
int[] nums = new int[26]; // 26个小写的英文字母
Arrays.fill(nums, -1);
for (int i = 0; i < equations.length; i++) {
char ch1 = equations[i].charAt(0);
char ch2 = equations[i].charAt(3);
if (equations[i].charAt(1) == '=') {
union(nums, ch1-'a', ch2-'a');
}
}
for (int i = 0; i < equations.length; i++) {
char ch1 = equations[i].charAt(0);
char ch2 = equations[i].charAt(3);
if (equations[i].charAt(1) == '!') {
if (isSameSet(nums, ch1-'a', ch2-'a')) {
return false;
}
}
}
return true;
}
private boolean isSameSet(int[] nums, int i, int j) {
return findRoot(nums, i) == findRoot(nums, j);
}
private void union(int[] nums, int i, int j) {
int index1 = findRoot(nums, i);
int index2 = findRoot(nums, j);
if (index1 == index2) {
return;
}
if (index1 < index2) {
nums[index1] += nums[index2];
nums[index2] = index1;
} else {
nums[index2] += nums[index1];
nums[index1] = index2;
}
}
private int findRoot(int[] nums, int i) {
while (nums[i] >= 0) {
i = nums[i];
}
return i;
}好啦！本期 数据结构之并查集 的学习之旅就到此结束啦！我们下一期再一起学习吧！