leetcode112. 路径总和 & leetcode113. 路径总和II，图文并茂，教你完全弄懂DFS，附详细代码

leetcode112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

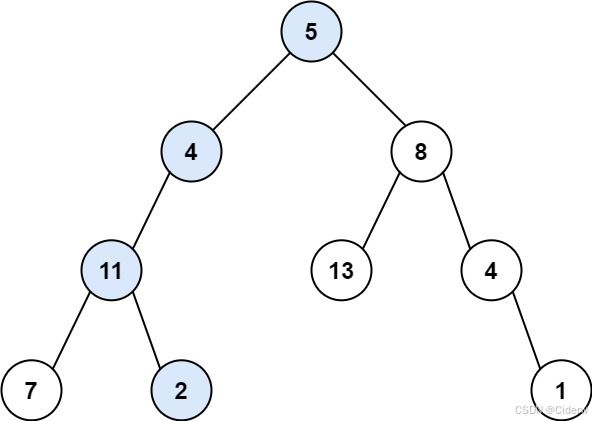
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

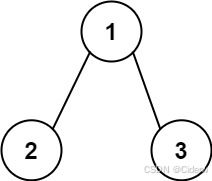
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

算法思路

使用深度优先搜索（DFS）遍历二叉树的每个节点，检查从根节点到每个叶子节点的路径和是否等于 sum。
所谓DFS，就是尽可能走远走深，如下图所示。

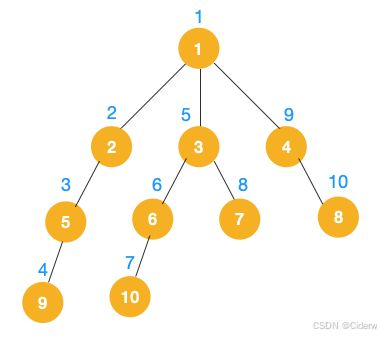
DFS

深度优先搜索（DFS）是一种用于遍历或搜索树结构和图的算法。它遵循以下综述规则：

起始点：从树或图的起始节点开始搜索。

分支探索：沿着树或图的分支尽可能深地搜索，直到到达末端节点（在树中是叶子节点，在图中是没有出边的节点）。
回溯：当到达末端节点后，搜索会回溯到上一个分支点，然后尝试其他未探索的分支。
遍历顺序：DFS没有固定的遍历顺序，它依赖于节点的访问顺序，这通常由算法的实现决定。
栈的使用：DFS通常使用栈数据结构来实现，无论是显式地使用栈还是通过递归调用堆栈隐式地使用。
递归实现：DFS可以通过递归函数实现，递归函数在每次到达末端节点时自动回溯。
应用场景：DFS适用于寻找路径、检测连通性、求解迷宫问题、拓扑排序等场景。
性能：DFS的时间复杂度为O(V+E)，在树中为O(N)，其中V是顶点数，E是边数，在树中N是节点数。
空间复杂度：DFS的空间复杂度主要取决于栈的深度，最坏情况下为O(N)。
非确定性：DFS在搜索过程中可能会遇到多个可能的路径，但它一次只探索一条路径。
全局与局部：在某些实现中，DFS可能需要使用全局变量来存储搜索状态，但这在多线程环境中可能不合适。
剪枝：在搜索过程中，可以根据问题的特性进行剪枝，即在确定某条路径不可能是解的情况下提前终止搜索。
后继节点的选择：在每次递归调用时，可以选择访问左子节点或右子节点，这通常取决于特定的问题和算法实现。
结束条件：搜索结束的条件可以是找到目标、遍历完所有节点或确定不存在解决方案。

具体可以看一下我之前的暴力搜索dfs的例题详细题解

算法步骤

初始化：定义一个全局变量 flag 初始值为 0，表示未找到符合条件的路径。
递归函数 dfs：
参数：当前节点 node 和当前路径的剩余目标和 target。
逻辑：
如果 flag 已经为 1，则直接返回，表示已经找到符合条件的路径。
如果当前节点是叶子节点（即没有左右子节点），则检查当前节点的值是否等于 target。如果是，则将 flag 设置为 1 并返回。
如果当前节点有左子节点，递归调用 dfs 函数，传入左子节点和更新后的 target（即当前目标和减去当前节点的值）。
同理，如果当前节点有右子节点，递归调用 dfs 函数，传入右子节点和更新后的 target。

具体代码

class Solution {
public:
    int flag=0;
    void dfs(TreeNode* node,int target)
    {
        if(flag==1) return;
        if(node->left==NULL && node->right==NULL)
        {
            if(target==node->val)
            {
                flag=1;
                return ;
            }
            return ;
        }
        if(node->left) dfs(node->left,target-node->val);
        if(node->right) dfs(node->right,target-node->val);
    }
    bool hasPathSum(TreeNode* root, int sum) {
        if(root==NULL) return false;
        dfs(root,sum);
        if(flag) return true;
        else return false;
    }
};

leetcode113. 路径总和II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

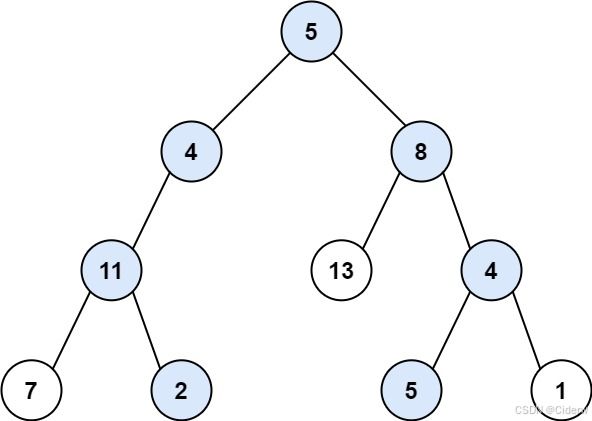
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：
输入：root = [1,2], targetSum = 0
输出：[]

大致思路和路径总和是一样的。但多了一步是将当前节点的值添加到path中，也就是保存了遍历的节点，并在递归调用结束后，将当前节点的值从path中删除，来回溯到上一个节点。

算法思路

基础条件：如果当前节点为空，则直接返回。
添加节点：将当前节点的值添加到path中。
更新目标和：从targetSum中减去当前节点的值。
检查叶子节点：如果当前节点是叶子节点（即没有左右子节点），并且剩余的目标和为0，则将当前路径添加到ret中。
递归搜索：递归调用dfs函数，分别搜索左子树和右子树。
回溯：在递归调用结束后，将当前节点的值从path中移除，以便回溯到上一个节点继续搜索。

具体代码

class Solution {
public:
    vector<vector<int>> ret;
    vector<int> path;

    void dfs(TreeNode* root, int targetSum) {
         if (root->left == nullptr && root->right == nullptr) {
            path.emplace_back(root->val);
            if(targetSum == root->val) 
            {
                ret.emplace_back(path);
            }
            return ;
        }
        path.emplace_back(root->val);
        if(root->left) 
        {
            dfs(root->left, targetSum - root->val);
            path.pop_back();
        }
        if(root->right) 
        {
            dfs(root->right, targetSum - root->val);
            path.pop_back();
        }
    }

    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root==nullptr) return ret;
        dfs(root, targetSum);
        return ret;
    }
};

做完此题，还可以看这类题的终极版。

leetcode437	路径总和III

• 我之后也会给出题解