- AI人工智能深度学习算法:搭建可拓展的深度学习模型架构
AI天才研究院
大数据AI人工智能AI大模型企业级应用开发实战大厂Offer收割机面试题简历程序员读书硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
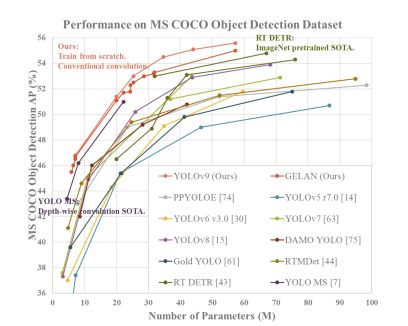
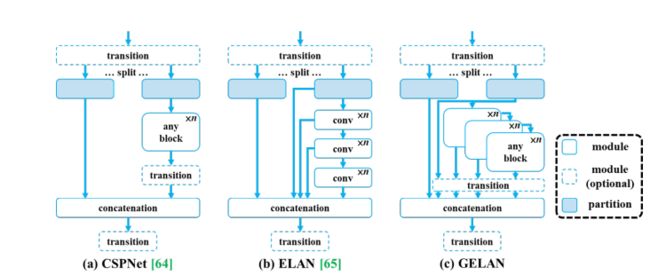
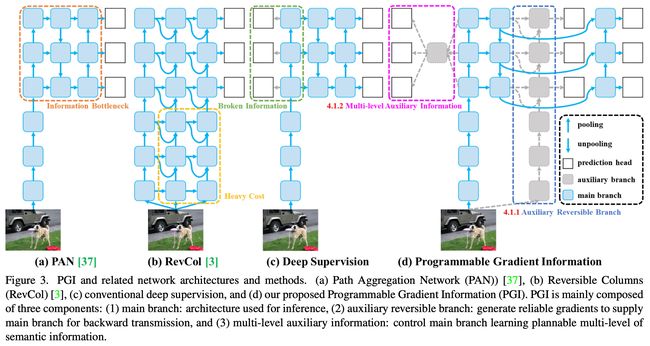
AI人工智能深度学习算法:搭建可拓展的深度学习模型架构作者:禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展,深度学习作为其主要驱动力之一,已经在各个领域取得了显著的成果。然而,随着模型规模的不断扩大,如何高效地搭建、训练和部署深度学习模型,成为一个亟待解决的问题。传统的单机训练方式在计算资源有限的情况
- LeetCode - #195 Swift 实现打印文件中的第十行
网罗开发
Swiftvue.jsleetcodeswift
网罗开发(小红书、快手、视频号同名) 大家好,我是展菲,目前在上市企业从事人工智能项目研发管理工作,平时热衷于分享各种编程领域的软硬技能知识以及前沿技术,包括iOS、前端、HarmonyOS、Java、Python等方向。在移动端开发、鸿蒙开发、物联网、嵌入式、云原生、开源等领域有深厚造诣。图书作者:《ESP32-C3物联网工程开发实战》图书作者:《SwiftUI入门,进阶与实战》超级个体:CO
- # 第一章:认识chatgpt
出门喝奶茶
chatgptchatgpt
chatgpt发展背景详细介绍一、基础理论背景人工智能和自然语言处理的兴起早期理论:20世纪中期,人工智能(AI)初见端倪,目标是模拟人类智能。自然语言处理作为AI的重要分支,致力于让机器理解和生成人类语言。关键里程碑:1980年代的统计方法和2000年代的神经网络技术,使NLP实现了从规则驱动到数据驱动的转变。神经网络与深度学习2010年代,深度学习的兴起极大推动了NLP的发展。基于大规模语料库
- 机器学习&深度学习目录
UQI-LIUWJ
各专栏目录深度学习人工智能1024程序员节
机器学习模型机器学习笔记:Transformer_刘文巾的博客-CSDN博客attention相关机器学习笔记:attention_UQI-LIUWJ的博客-CSDN博客机器学习笔记:ELMOBERT_UQI-LIUWJ的博客-CSDN博客机器学习笔记:ViT(论文AnImageIsWorth16X16Words:TransformersforImageRecognitionatScale)_UQ
- 影视制作的未来:云渲染+虚拟制作+AI生成技术
LhcyyVSO
AIGC云渲染影视动画人工智能3d云渲染渲染农场AIAICG虚拟制作
在计算机技术和人工智能技术飞速发展的2024年,影视制作正在经历一场前所未有的变革。云渲染、虚拟制作和AI生成等新影视制作技术的结合,正在重新定义数字内容的创作流程,为影视产业带来了全新的可能性和机遇。这些前沿技术不仅提高了制作效率,还打开了无限的创作空间,有望引领未来的影视制作走向新的高峰。云渲染:加速创意实现影视的后期特效制作阶段需要大量的计算机参与渲染。传统的渲染过程耗时长且成本高,而云渲染
- 打造你的聊天助手:使用C#、OpenAI和Spectre.Console创建控制台ChatGPT客户端
墨夶
C#学习资料1c#chatgpt开发语言
打造你的聊天助手:使用C#、OpenAI和Spectre.Console创建控制台ChatGPT客户端在这个人工智能飞速发展的时代,ChatGPT以其卓越的对话能力和智能回答在聊天领域引起了革命。你是否想过将这种能力融入到你的控制台应用中,让命令行界面也能拥有智能对话的体验?本文将带你一步步使用C#、OpenAI的API和Spectre.Console库,创建一个功能强大的控制台ChatGPT客户
- 软件测试中的AI-为什么它在软件自动化测试中很重要?
测试界霄霄
软件测试人工智能功能测试自动化测试软件测试程序人生职场和发展
通俗地说,人工智能(AI)是计算机科学的一个领域,它专注于使机器“智能化”。所谓智能,就是使系统能够像人类一样学习和做出决策。因此,人工智能机器将能够学习如何在特定情况下做出反应,然后根据其学习情况在未来场景中做出决策。人工智能(AI)在大多数领域的应用仍处于早期阶段,想要完美运行还需要很长时间。今天的人工智能(AI)技术可以帮助我们完成许多不需要复杂思考的重复性日常任务。接下来,让我们讨论软件测
- 遥感深度学习过程中图像分割的尺寸对模型训练结果的影响
司南锤
深度学习遥感深度学习人工智能
1.计算资源与显存占用大尺寸图像:需要更高的显存和计算资源,可能限制训练时的批大小(batchsize),甚至导致无法训练。解决方案:通常将大图裁剪为小尺寸的补丁(patches),例如256x256或512x512。小尺寸图像:显存占用低,但可能丢失全局上下文信息(如大面积地物分布),影响模型对复杂场景的理解。2.模型感受野与上下文信息小尺寸输入:模型感受野受限,可能无法捕捉大范围地物(如河流、
- 在计算机上本地运行 Deepseek R1
itmanll
linux
DownloadOllamaonLinuxDownloadOllamaonWindowsDownloadOllamaonmacOSDeepseekR1是一个强大的人工智能模型,在科技界掀起了波澜。它是一个开源语言模型,可以与GPT-4等大玩家展开竞争。但更重要的是,与其他一些模型不同,您可以在自己的计算机上本地运行DeepseekR1。linux步骤第1步:下载Ollama并安装curl-fsSL
- #深度学习:从基础到实践
single_ffish
深度学习gpt神经网络生成对抗网络1024程序员节
深度学习是人工智能领域近年来最为火热的技术之一。它通过构建由多个隐藏层组成的神经网络模型,能够从海量数据中自动学习特征和表征,在图像识别、自然语言处理、语音识别等领域取得了突破性进展。本文将全面介绍深度学习的基础知识、主要算法和实践应用,帮助您快速掌握这一前沿技术。1.深度学习的基础1.1人工神经网络深度学习是基于人工神经网络(ArtificialNeuralNetwork,ANN)的一种机器学习
- 【深度学习|地学应用】遥感与深度学习:揭示梦柯冰川奥秘的前沿应用与实践解析
985小水博一枚呀
深度学习地学应用深度学习人工智能
【深度学习|地学应用】遥感与深度学习:揭示梦柯冰川奥秘的前沿应用与实践解析【深度学习|地学应用】遥感与深度学习:揭示梦柯冰川奥秘的前沿应用与实践解析文章目录【深度学习|地学应用】遥感与深度学习:揭示梦柯冰川奥秘的前沿应用与实践解析前言一、使用高分6号遥感影像结合深度学习对梦柯冰川的研究方向1.冰川边界自动化提取2.冰川变化动态监测3.冰川分类与分布特征分析二、梦柯冰川(MunkuGlacier)的
- 机器学习入门——机器学习基本概念
四月是你的
机器学习
@机器学习什么是机器学习机器学习(MachineLearning,ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎简单来说机器学习就是机
- 基于R-CNN深度学习的无人机目标检测系统:数据集、模型和UI界面的完整实现
2025年数学建模美赛
R-CNN检测系统深度学习cnn无人机计算机视觉目标检测人工智能
摘要随着无人机技术的迅猛发展,无人机在军事、农业、环境监测等多个领域的应用日益广泛。无人机目标检测系统的建设成为提升无人机自主飞行和环境感知能力的重要环节。本文将详细介绍如何构建一个基于深度学习的无人机目标检测系统,采用R-CNN(区域卷积神经网络)算法,通过用户界面设计和数据集处理,实现高效的目标检测功能。通过本项目,旨在为无人机目标检测提供一种可行的解决方案,并提高其在复杂环境下的工作效率。目
- 基于Multi-Agent的无人机集群体系自主作战系统设计
龙腾亚太
无人机
源自:系统工程与电子技术作者:张堃,华帅,袁斌林,杜睿怡“人工智能技术与咨询”发布摘要针对无人集群自主作战体系设计中的关键问题,提出基于Multi-Agent的无人集群自主作战系统设计方法。建立无人集群各节点的Agent模型及其推演规则;对于仿真系统模块化和通用化的需求,设计系统互操作式接口和无人集群自主作战的交互关系;开展无人集群系统仿真推演验证。仿真结果表明,所提设计方案不仅能够有效开展并完成
- 用 Neo4j GraphRAG 工具开启你的智能应用之旅
步子哥
AGI通用人工智能neo4j人工智能
在这个人工智能飞速发展的时代,Neo4j带来了一项令人激动的创新——GraphRAG生态系统工具。这组开源工具为开发人员提供了一个全新的途径,以构建基于知识图谱的智能应用,让机器更好地理解和回应我们的查询。接下来,让我们一起探索这些工具如何帮助我们构建更智能、更准确的应用。什么是GraphRAG?GraphRAG是一种结合了检索增强生成(RAG)技术和知识图谱的解决方案。它不仅解决了大型语言模型常
- 探索未来对话的边界:Mixture-of-Agents(MoA)——大型语言模型的集体智慧引擎
潘俭渝Erik
探索未来对话的边界:Mixture-of-Agents(MoA)——大型语言模型的集体智慧引擎项目地址:https://gitcode.com/gh_mirrors/mo/MoA在当前人工智能的浪潮中,我们迎来了一个令人兴奋的技术突破——Mixture-of-Agents(MoA),它标志着大型语言模型(LLM)能力提升的新纪元。本文将引领您深入探索这一革命性项目,揭示其技术精粹,展望应用前景,并
- 【Python】已解决:error: subprocess-exited-with-error
屿小夏
python开发语言linux
个人简介:某不知名博主,致力于全栈领域的优质博客分享|用最优质的内容带来最舒适的阅读体验!文末获取免费IT学习资料!文末获取更多信息精彩专栏推荐订阅收藏专栏系列直达链接相关介绍书籍分享点我跳转书籍作为获取知识的重要途径,对于IT从业者来说更是不可或缺的资源。不定期更新IT图书,并在评论区抽取随机粉丝,书籍免费包邮到家AI前沿点我跳转探讨人工智能技术领域的最新发展和创新,涵盖机器学习、深度学习、自然
- 探索人工智能在计算机视觉领域的创新应用与挑战
戒了9
人工智能学习方法
一、引言1.1研究背景与意义在科技飞速发展的当下,人工智能(ArtificialIntelligence,AI)已然成为引领新一轮科技革命和产业变革的重要驱动力。作为AI领域的关键分支,计算机视觉(ComputerVision,CV)致力于让计算机具备像人类一样理解和解析图像、视频等视觉信息的能力,近年来取得了令人瞩目的进展。二者的深度融合,更是为众多领域带来了前所未有的变革与机遇。从技术发展历程
- 人工智能前沿技术进展与应用前景探究
戒了9
人工智能搜索引擎百度
一、引言1.1研究背景与意义人工智能作为一门极具变革性的前沿技术,正深刻地改变着人类社会的各个层面。从其诞生之初,人工智能便承载着人类对智能机器的无限遐想与探索。自20世纪中叶起,人工智能踏上了它的发展征程,历经了多个重要阶段,每一阶段都伴随着理论的突破、技术的革新以及应用领域的拓展。在初级阶段(1943-1956),沃伦・麦卡洛克和沃尔特・皮茨提出的人工神经网络基本模型,为人工智能的发展奠定了初
- chatgpt赋能python:Python如何删除一个对象
atest166
ChatGptchatgptjvmjava计算机
Python如何删除一个对象Python是一种高级、面向对象、动态类型解释型语言,它有广泛的应用,尤其在数据分析、机器学习、人工智能和Web开发等领域。但是,在Python编程过程中,我们也可能需要删除对象。那么,Python如何删除一个对象呢?Python对象和变量在Python中,一切都是对象。对象是内存中的一块数据,有自己的身份、类型和值。变量是指向对象的引用,通过变量可以访问对象的属性和方
- 人工智能前沿技术进展与应用前景探究
戒了9
搜索引擎
一、引言1.1研究背景与意义人工智能作为一门极具变革性的前沿技术,正深刻地改变着人类社会的各个层面。从其诞生之初,人工智能便承载着人类对智能机器的无限遐想与探索。自20世纪中叶起,人工智能踏上了它的发展征程,历经了多个重要阶段,每一阶段都伴随着理论的突破、技术的革新以及应用领域的拓展。在初级阶段(1943-1956),沃伦・麦卡洛克和沃尔特・皮茨提出的人工神经网络基本模型,为人工智能的发展奠定了初
- 探索 Meissonic:文本到图像生成的新星
zhangjiaofa
大模型文生图大模型Meissonic
目录前言模型概述主要功能技术架构应用场景在线体验本地部署克隆存储库创建虚拟环境安装扩散器启动GradioWeb用户界面文本到图像生成结语项目地址一、前言在人工智能迅猛发展的今天,文本到图像生成技术已成为科技前沿的热点。从艺术创作到商业设计,从学术研究到工业应用,这一技术正以惊人的速度改变着我们与数字内容的交互方式。众多研究机构和企业纷纷投入这一领域,不断推动技术的边界。然而,尽管已有许多优秀的模型
- AI在电商平台商品描述生成中的应用
AI天才研究院
计算AI大模型企业级应用开发实战大数据AI人工智能javapythonjavascriptkotlingolang架构人工智能大厂程序员硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLM系统架构设计软件哲学Agent程序员实现财富自由
AI在电商平台商品描述生成中的应用关键词:人工智能、电商平台、商品描述、自然语言处理、机器学习、深度学习摘要:本文深入探讨了人工智能在电商平台商品描述生成中的应用。首先,我们回顾了人工智能的概述和电商平台的发展背景。随后,分析了商品描述在电商平台中的重要性以及存在的问题。接下来,我们重点介绍了AI在商品描述生成中的应用技术,包括自然语言处理、机器学习和深度学习等。文章还通过实战案例展示了AI商品描
- SpringAI基于API对大语言模型调用
_沉浮_
AI语言模型人工智能springAI
引言随着人工智能技术的迅猛发展,大型语言模型(LLM)在各个领域的应用越来越广泛。SpringAI作为一个旨在简化AI集成的框架,为开发者提供了高效、便捷的工具来连接和调用这些大模型。本文将详细探讨如何使用SpringAI整合通义千问等大语言模型,并通过实例演示这一过程,最后提供一些扩展建议。一、SpringAI简介SpringAI是一个专为AI工程设计的应用框架,旨在将Spring生态系统设计原
- 【Python】已解决:(cmd进入Python环境报错)No Python at ‘C:\Users…\Python\Python39\python.exe’
屿小夏
pythonlinux开发语言
个人简介:某不知名博主,致力于全栈领域的优质博客分享|用最优质的内容带来最舒适的阅读体验!文末获取免费IT学习资料!文末获取更多信息精彩专栏推荐订阅收藏专栏系列直达链接相关介绍书籍分享点我跳转书籍作为获取知识的重要途径,对于IT从业者来说更是不可或缺的资源。不定期更新IT图书,并在评论区抽取随机粉丝,书籍免费包邮到家AI前沿点我跳转探讨人工智能技术领域的最新发展和创新,涵盖机器学习、深度学习、自然
- 深度学习之基于Django+YOLOv5商标识别
Q1744828575
pythonplotlypython
欢迎大家点赞、收藏、关注、评论啦,由于篇幅有限,只展示了部分核心代码。文章目录一项目简介二、功能三、系统四.总结一项目简介 一、项目背景在数字化时代,商标作为企业的重要资产,其保护和管理显得尤为重要。然而,传统的商标识别方法往往依赖于人工审查,效率低下且容易出错。随着深度学习技术的不断发展,尤其是目标检测领域的进步,自动化、高精度的商标识别成为可能。本项目旨在利用DjangoWeb框架和YOLO
- ERROR: Could not install packages due to an OSError: [Errno 2] No such file or directory解决方案
爱编程的喵喵
Python基础课程pythonpipOSError解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理解,而且能够帮助新手快速入门。 本文主要介绍了ERROR:Couldnotinst
- 安装flash-attn出现RuntimeError current installed version g++ (4.8.5) is less than mininum version解决方案
爱编程的喵喵
Python基础课程pythonflash-attng++RuntimeError
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。 本文主要介绍了安装flash-attn出现RuntimeErrorcurrentinstalledversiong++(4.8.5)islessthanmininumversion解决方案
- 动手学深度学习-卷积神经网络-3填充和步幅
像污秽一样
动手学深度学习深度学习cnn人工智能神经网络
目录填充步幅小结在上一节的例子(下图)中,输入的高度和宽度都为3,卷积核的高度和宽度都为2,生成的输出表征的维数为2×2。正如我们在上一节中所概括的那样,假设输入形状为nh×nw,卷积核形状为kh×kw,那么输出形状将是(nh−kh+1)×(nw−kw+1)。因此,卷积的输出形状取决于输入形状和卷积核的形状。还有什么因素会影响输出的大小呢?本节我们将介绍填充(padding)和步幅(stride)
- 9.6 解锁 AI 潜力:GPT Builder 的强大能力与无限可能
少林码僧
AI大模型应用实战专栏人工智能gpt
解锁AI潜力:GPTBuilder的强大能力与无限可能引言:轻松打造智能应用的革命性工具在人工智能的浪潮中,GPTBuilder作为一款强大且易用的开发工具,让构建AI驱动的智能应用变得前所未有的简单。无论你是开发者、企业家,还是对技术一知半解的创作者,GPTBuilder都能帮助你快速将创意变为现实。从自动化客户支持到内容生成,从数据分析到智能助手,GPTBuilder提供了丰富的功能和灵活的设
- 多线程编程之join()方法
周凡杨
javaJOIN多线程编程线程
现实生活中,有些工作是需要团队中成员依次完成的,这就涉及到了一个顺序问题。现在有T1、T2、T3三个工人,如何保证T2在T1执行完后执行,T3在T2执行完后执行?问题分析:首先问题中有三个实体,T1、T2、T3, 因为是多线程编程,所以都要设计成线程类。关键是怎么保证线程能依次执行完呢?
Java实现过程如下:
public class T1 implements Runnabl
- java中switch的使用
bingyingao
javaenumbreakcontinue
java中的switch仅支持case条件仅支持int、enum两种类型。
用enum的时候,不能直接写下列形式。
switch (timeType) {
case ProdtransTimeTypeEnum.DAILY:
break;
default:
br
- hive having count 不能去重
daizj
hive去重having count计数
hive在使用having count()是,不支持去重计数
hive (default)> select imei from t_test_phonenum where ds=20150701 group by imei having count(distinct phone_num)>1 limit 10;
FAILED: SemanticExcep
- WebSphere对JSP的缓存
周凡杨
WAS JSP 缓存
对于线网上的工程,更新JSP到WebSphere后,有时会出现修改的jsp没有起作用,特别是改变了某jsp的样式后,在页面中没看到效果,这主要就是由于websphere中缓存的缘故,这就要清除WebSphere中jsp缓存。要清除WebSphere中JSP的缓存,就要找到WAS安装后的根目录。
现服务
- 设计模式总结
朱辉辉33
java设计模式
1.工厂模式
1.1 工厂方法模式 (由一个工厂类管理构造方法)
1.1.1普通工厂模式(一个工厂类中只有一个方法)
1.1.2多工厂模式(一个工厂类中有多个方法)
1.1.3静态工厂模式(将工厂类中的方法变成静态方法)
&n
- 实例:供应商管理报表需求调研报告
老A不折腾
finereport报表系统报表软件信息化选型
引言
随着企业集团的生产规模扩张,为支撑全球供应链管理,对于供应商的管理和采购过程的监控已经不局限于简单的交付以及价格的管理,目前采购及供应商管理各个环节的操作分别在不同的系统下进行,而各个数据源都独立存在,无法提供统一的数据支持;因此,为了实现对于数据分析以提供采购决策,建立报表体系成为必须。 业务目标
1、通过报表为采购决策提供数据分析与支撑
2、对供应商进行综合评估以及管理,合理管理和
- mysql
林鹤霄
转载源:http://blog.sina.com.cn/s/blog_4f925fc30100rx5l.html
mysql -uroot -p
ERROR 1045 (28000): Access denied for user 'root'@'localhost' (using password: YES)
[root@centos var]# service mysql
- Linux下多线程堆栈查看工具(pstree、ps、pstack)
aigo
linux
原文:http://blog.csdn.net/yfkiss/article/details/6729364
1. pstree
pstree以树结构显示进程$ pstree -p work | grep adsshd(22669)---bash(22670)---ad_preprocess(4551)-+-{ad_preprocess}(4552) &n
- html input与textarea 值改变事件
alxw4616
JavaScript
// 文本输入框(input) 文本域(textarea)值改变事件
// onpropertychange(IE) oninput(w3c)
$('input,textarea').on('propertychange input', function(event) {
console.log($(this).val())
});
- String类的基本用法
百合不是茶
String
字符串的用法;
// 根据字节数组创建字符串
byte[] by = { 'a', 'b', 'c', 'd' };
String newByteString = new String(by);
1,length() 获取字符串的长度
&nbs
- JDK1.5 Semaphore实例
bijian1013
javathreadjava多线程Semaphore
Semaphore类
一个计数信号量。从概念上讲,信号量维护了一个许可集合。如有必要,在许可可用前会阻塞每一个 acquire(),然后再获取该许可。每个 release() 添加一个许可,从而可能释放一个正在阻塞的获取者。但是,不使用实际的许可对象,Semaphore 只对可用许可的号码进行计数,并采取相应的行动。
S
- 使用GZip来压缩传输量
bijian1013
javaGZip
启动GZip压缩要用到一个开源的Filter:PJL Compressing Filter。这个Filter自1.5.0开始该工程开始构建于JDK5.0,因此在JDK1.4环境下只能使用1.4.6。
PJL Compressi
- 【Java范型三】Java范型详解之范型类型通配符
bit1129
java
定义如下一个简单的范型类,
package com.tom.lang.generics;
public class Generics<T> {
private T value;
public Generics(T value) {
this.value = value;
}
}
- 【Hadoop十二】HDFS常用命令
bit1129
hadoop
1. 修改日志文件查看器
hdfs oev -i edits_0000000000000000081-0000000000000000089 -o edits.xml
cat edits.xml
修改日志文件转储为xml格式的edits.xml文件,其中每条RECORD就是一个操作事务日志
2. fsimage查看HDFS中的块信息等
&nb
- 怎样区别nginx中rewrite时break和last
ronin47
在使用nginx配置rewrite中经常会遇到有的地方用last并不能工作,换成break就可以,其中的原理是对于根目录的理解有所区别,按我的测试结果大致是这样的。
location /
{
proxy_pass http://test;
- java-21.中兴面试题 输入两个整数 n 和 m ,从数列 1 , 2 , 3.......n 中随意取几个数 , 使其和等于 m
bylijinnan
java
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class CombinationToSum {
/*
第21 题
2010 年中兴面试题
编程求解:
输入两个整数 n 和 m ,从数列 1 , 2 , 3.......n 中随意取几个数 ,
使其和等
- eclipse svn 帐号密码修改问题
开窍的石头
eclipseSVNsvn帐号密码修改
问题描述:
Eclipse的SVN插件Subclipse做得很好,在svn操作方面提供了很强大丰富的功能。但到目前为止,该插件对svn用户的概念极为淡薄,不但不能方便地切换用户,而且一旦用户的帐号、密码保存之后,就无法再变更了。
解决思路:
删除subclipse记录的帐号、密码信息,重新输入
- [电子商务]传统商务活动与互联网的结合
comsci
电子商务
某一个传统名牌产品,过去销售的地点就在某些特定的地区和阶层,现在进入互联网之后,用户的数量群突然扩大了无数倍,但是,这种产品潜在的劣势也被放大了无数倍,这种销售利润与经营风险同步放大的效应,在最近几年将会频繁出现。。。。
如何避免销售量和利润率增加的
- java 解析 properties-使用 Properties-可以指定配置文件路径
cuityang
javaproperties
#mq
xdr.mq.url=tcp://192.168.100.15:61618;
import java.io.IOException;
import java.util.Properties;
public class Test {
String conf = "log4j.properties";
private static final
- Java核心问题集锦
darrenzhu
java基础核心难点
注意,这里的参考文章基本来自Effective Java和jdk源码
1)ConcurrentModificationException
当你用for each遍历一个list时,如果你在循环主体代码中修改list中的元素,将会得到这个Exception,解决的办法是:
1)用listIterator, 它支持在遍历的过程中修改元素,
2)不用listIterator, new一个
- 1分钟学会Markdown语法
dcj3sjt126com
markdown
markdown 简明语法 基本符号
*,-,+ 3个符号效果都一样,这3个符号被称为 Markdown符号
空白行表示另起一个段落
`是表示inline代码,tab是用来标记 代码段,分别对应html的code,pre标签
换行
单一段落( <p>) 用一个空白行
连续两个空格 会变成一个 <br>
连续3个符号,然后是空行
- Gson使用二(GsonBuilder)
eksliang
jsongsonGsonBuilder
转载请出自出处:http://eksliang.iteye.com/blog/2175473 一.概述
GsonBuilder用来定制java跟json之间的转换格式
二.基本使用
实体测试类:
温馨提示:默认情况下@Expose注解是不起作用的,除非你用GsonBuilder创建Gson的时候调用了GsonBuilder.excludeField
- 报ClassNotFoundException: Didn't find class "...Activity" on path: DexPathList
gundumw100
android
有一个工程,本来运行是正常的,我想把它移植到另一台PC上,结果报:
java.lang.RuntimeException: Unable to instantiate activity ComponentInfo{com.mobovip.bgr/com.mobovip.bgr.MainActivity}: java.lang.ClassNotFoundException: Didn't f
- JavaWeb之JSP指令
ihuning
javaweb
要点
JSP指令简介
page指令
include指令
JSP指令简介
JSP指令(directive)是为JSP引擎而设计的,它们并不直接产生任何可见输出,而只是告诉引擎如何处理JSP页面中的其余部分。
JSP指令的基本语法格式:
<%@ 指令 属性名="
- mac上编译FFmpeg跑ios
啸笑天
ffmpeg
1、下载文件:https://github.com/libav/gas-preprocessor, 复制gas-preprocessor.pl到/usr/local/bin/下, 修改文件权限:chmod 777 /usr/local/bin/gas-preprocessor.pl
2、安装yasm-1.2.0
curl http://www.tortall.net/projects/yasm
- sql mysql oracle中字符串连接
macroli
oraclesqlmysqlSQL Server
有的时候,我们有需要将由不同栏位获得的资料串连在一起。每一种资料库都有提供方法来达到这个目的:
MySQL: CONCAT()
Oracle: CONCAT(), ||
SQL Server: +
CONCAT() 的语法如下:
Mysql 中 CONCAT(字串1, 字串2, 字串3, ...): 将字串1、字串2、字串3,等字串连在一起。
请注意,Oracle的CON
- Git fatal: unab SSL certificate problem: unable to get local issuer ce rtificate
qiaolevip
学习永无止境每天进步一点点git纵观千象
// 报错如下:
$ git pull origin master
fatal: unable to access 'https://git.xxx.com/': SSL certificate problem: unable to get local issuer ce
rtificate
// 原因:
由于git最新版默认使用ssl安全验证,但是我们是使用的git未设
- windows命令行设置wifi
surfingll
windowswifi笔记本wifi
还没有讨厌无线wifi的无尽广告么,还在耐心等待它慢慢启动么
教你命令行设置 笔记本电脑wifi:
1、开启wifi命令
netsh wlan set hostednetwork mode=allow ssid=surf8 key=bb123456
netsh wlan start hostednetwork
pause
其中pause是等待输入,可以去掉
2、
- Linux(Ubuntu)下安装sysv-rc-conf
wmlJava
linuxubuntusysv-rc-conf
安装:sudo apt-get install sysv-rc-conf 使用:sudo sysv-rc-conf
操作界面十分简洁,你可以用鼠标点击,也可以用键盘方向键定位,用空格键选择,用Ctrl+N翻下一页,用Ctrl+P翻上一页,用Q退出。
背景知识
sysv-rc-conf是一个强大的服务管理程序,群众的意见是sysv-rc-conf比chkconf
- svn切换环境,重发布应用多了javaee标签前缀
zengshaotao
javaee
更换了开发环境,从杭州,改变到了上海。svn的地址肯定要切换的,切换之前需要将原svn自带的.svn文件信息删除,可手动删除,也可通过废弃原来的svn位置提示删除.svn时删除。
然后就是按照最新的svn地址和规范建立相关的目录信息,再将原来的纯代码信息上传到新的环境。然后再重新检出,这样每次修改后就可以看到哪些文件被修改过,这对于增量发布的规范特别有用。
检出