Codeforces Round 938 (Div. 3)A-C,E-H
题目链接
A. Yogurt Sale
贪心的选两个物品价格少的,若总个数为奇数再加是单个价格
代码:
#include
#define ll long long
using namespace std;
void solve(){
int n,a,b;
cin>>n>>a>>b;
int r=0;
if(n&1){
if(b>t;
while(t--){
solve();
}
return 0;
} B. Progressive Square
因为c,d大于0,所以不管是行还是列都是单调递增的,也就是说a[1][1]一定是最小的,
那么就按照最小的数开始构造,若不存在则不合法,可能有相等的数,所以用个map
记录数量。
代码:
#include
#define ll long long
using namespace std;
int c[510*510];
void solve(){
int n,a,b;
cin>>n>>a>>b;
map v;
for(int i=1;i<=n*n;i++){
cin>>c[i];
v[c[i]]++;
}
int f=0,j=(*v.begin()).first;
for(int i=1;i<=n;i++){
if(v[j]==0) f=1;
v[j]--;
for(int k=1;k>t;
while(t--){
solve();
}
return 0;
} C. Inhabitant of the Deep Sea
按照题目模拟即可,每次减去a[l],a[r]之间最小的数,这样时间是o(n)的。对于退出
条件就是当前两数的最小值大于等于k/2,表示会在两数消失前k为0(也可能k还剩下1),
这里有个注意点:退出条件里的l可能会向右走两个位置,可能会到n+1的位置,如果
数据没有初始化就会wa,要么初始化,要么将第二个l++放在if条件里。
代码:
#include
#define ll long long
using namespace std;
const int N=2e5+10;
ll a[N];
ll n,k;
void solve(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
}
if(n==1){
if(k>=a[1])
cout << "1" << endl;
else
cout << "0" << endl;
return;
}
int l=1,r=n;
while(1){
if(l>=r)break;
if(k/2<=min(a[l],a[r])){
int m=k/2;
a[l]-=m,a[r]-=m,k-=m*2;
if(a[l]==0)l++;
if(a[r]==0)r--;
if(k&&a[l]){
a[l]--,k--;
if(a[l]==0)
l++;}
break;
}
int u=min(a[l],a[r]);
a[l]-=u;a[r]-=u;k-=2*u;
if(a[l]==0) l++;
if(a[r]==0) r--;
if(l>=r) break;
}
// cout << "....." <0){
if(k>=a[l])
cout << n << endl;
else
cout << n-1 << endl;
return;
}
if(1){
cout << n-max(0,r-l+1) << endl;
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
} D. Inaccurate Subsequence Search
双指针模拟即可。
E. Long Inversions
数据最大5000,考虑直接枚举k(我不确定k是不是有单调性),check函数里用异或差分,
a[i]=s[i]^s[i-1],贪心的修改,若当前位置为0则进行修改,b[i]^=1,b[i+k]^=1,若i+k超出了
n就是不合法。
代码:
#include
#define ll long long
using namespace std;
const int N=4e5+10;
ll a[N],b[N];
ll n,k;
bool check(int k){
for(int i=0;i<=n;i++)
b[i]=a[i];
int r=0;
int f=1;
for(int i=0;in){
f=0;
}
b[i]^=1;
b[i+k]^=1;
r=1;
}
}
return f;
}
void solve(){
cin>>n;
string s;
cin>>s;
a[0]=s[0]-'0';
for(int i=1;i=1;k--){
if(check(k))
break;
}
cout << k << endl;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
} F. Unfair Game
容易发现4只受4影响,若4的个数不为偶数肯定异或值不为0。对于1,2,3,若他们异或值不为0先
把他们变成0。接下来有两种操作,将1,2,3个数都减1,或者将他们其中一个减2。假设1,2,3个数
都为2,前者操作次数为2,后者操作次数为3,所以贪心的选择后者操作。考虑2无法操作的时候,也就是1,2,3个数都为1,则进行一次前者操作。
代码:
#include
using namespace std;
const int N=3e6+10;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair pii;
typedef unsigned long long ull;
//const ll P=2281701377;
const ll P=998244353;
void solve(){
int a,b,c,d;
cin>>a>>b>>c>>d;
ll ans=0;
if(a%2&&b%2&&c%2)
ans++;
ans+=a/2;
ans+=b/2;
ans+=c/2;
ans+=d/2;
cout<>t;
while(t--){
solve();
}
}
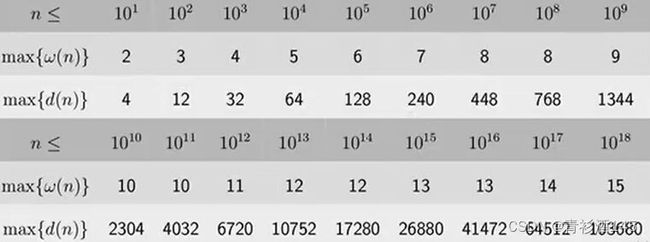
G. GCD on a grid
图片来源
1e6以内的数约数个数最多240,我们考虑暴力枚举约数。对于每个约数搜索能否到终点,
对于取约数的时候一定要用根号算法,用o(n)多组数据会超时。然后我写的dfs超时了,
用的bfs才过的。
代码:
#include
using namespace std;
const int N=3e6+10;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair pii;
typedef unsigned long long ull;
//const ll P=2281701377;
const ll P=998244353;
int vis[200][200];
vector v;
int n,m,f,tol;
int a[200][200];
int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
bool check(int k){
tol++;
f=0;
queue q;
q.push({1,1});
while(q.size()){
int x=q.front().first,y=q.front().second;
q.pop();
if(vis[x][y]==tol) continue;
vis[x][y]=tol;
if(x==n&&y==m){
f=1;
break;
}
if(y+1<=m&&vis[x][y+1]!=tol&&a[x][y+1]%k==0){
q.push({x,y+1});
}
if(x+1<=n&&vis[x+1][y]!=tol&&a[x+1][y]%k==0){
q.push({x+1,y});
}
}
return f;
}
void solve(){
v.clear();
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
cin>>a[i][j];
}
int g=gcd(a[1][1],a[n][m]);
for(int i=1;i<=sqrt(g);i++){
if(a[1][1]%i==0&&a[n][m]%i==0){
v.push_back(i);
v.push_back(g/i);
}
}
sort(v.begin(),v.end());
int ans=1;
for(int i=v.size()-1;i>=0;i--){
int j=v[i];
if(check(j)){
ans=j;break;
}
}
cout<>t;
while(t--){
solve();
}
}
H. The Most Reckless Defense
对于每个塔的距离增加贡献为w=p*x-3^y,p为该塔的攻击力,x为该距离范围内的路程距离,
y为攻击距离。贪心的考虑,当贡献为负数就不进行选择,容易发现贡献是呈指数减少的,
我们考虑y最大为13。我们可以先预处理出每个塔每个距离的贡献。由于题目说了每个距离只能
取一次,我们考虑状压dp,考虑第i个塔从没选第j个距离到第i个塔选了第j个距离时的贡献最大值
代码:
#include
using namespace std;
const int N=3e6+10;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair pii;
typedef unsigned long long ull;
//const ll P=2281701377;
const ll P=998244353;
int n,m,k;
ll dp[2][1<<13];
ll s[51*51][14];
char a[60][60];
double dis(int x,int y,pii z){
int xx=z.first,yy=z.second;
return sqrt((x-xx)*(x-xx)+(y-yy)*(y-yy));
}
void solve(){
cin>>n>>m>>k;
for(int i=0;i<2;i++){
for(int j=0;j<(1<<13);j++){
dp[i][j]=0;
}
}
vector v;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
if(a[i][j]=='#')
v.push_back({i,j});
}
}
for(int i=1;i<=k;i++){
int x,y,p;cin>>x>>y>>p;
ll bas=1;
for(int j=0;j<13;j++){
bas*=3;
int cnt=0;
for(int k=0;k>k)&(1)){
dp[op][j]=max(dp[op][j],dp[op^1][j^(1<>t;
while(t--){
solve();
}
}