poj 3270 Cow Sorting 置换

　　总共共10^5个数，取值在10^6之内

　　离散化后与下标形成映射，转换成置换群

　　然后就可以形成：

　　有 n = 10^5 个位置， 每个位置有一头编号为 a[i]  (取值范围为[1,n] ) 的牛， 其愤怒值为 dep[ a[i] ]

　　对于置换群求出其循环因子后. 因为置换的权值花费为 dep[i], dep[j]

　　所以我们取最小的 dep, 例如循环因子 ( 1 , 4, 7, 8 ) 需要三次置换 , 我们可以取最小的 1, 其愤怒值为 dep[1] ( 我们按权值递增离散化过)

　　所以三次置换分别为 ( 1, 4 ) ( 1, 7 ) ( 1, 8 )

　　则三次花费为  ( dep[1] + dep[4] ) + ( dep[1] + dep[7] ) +( dep[1] + dep[8] ) 

　　等价与  dep[1] * 3 + ( dep[7] + dep[8] + dep[4] )   

　　我们在找循环因子时,就可以计算出 总和以及 当前循环因子的最小值.  通过 dep[ Min ] * ( num-1 ) +  ( sum(当前循环因子愤怒值总和) -  dep[Min] ) 

　　其实这个思路是有问题的. 题目只要求最小花费,并未要求最小置换次数. 是否我们可能通过更多的置换得到 更少的花费呢.

　　我们看这组数据:

　　( 1 , 8 , 9, 7 , 6 )   

　　离散化后对应为 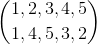　  ,   第一列为标准序列,第二列为当前序列. 

　　其循环因子为 ( 1 ) * ( 2 , 4, 3, 5 )  

　　对于 循环因子 ( 2, 4 , 3, 5 )  最小置换花费为   dep[2]*3 + ( dep[3]+dep[4]+dep[5] )  = 42

　　如果我们首先 把 1, 2 置换.  然后 对于 ( 1, 4, 3, 5 ) 进行置换, 之后再将 ( 1, 2 ) 置换回来总花费为  dep[1]*3 + ( dep[3]+dep[4]+dep[5] ) + 2*(dep[1]+dep[2) = 41

　　根据结果我们发现这样我们可以得到一个更优的解, 那么我们需要的结果就是当前 循环因子的最小值 与 整个置换群的 最小值间的对比了

　　假设当前循环因子最小dep值的下标为 p, 阶数为 n,  则 当前循环因子最优结果为

　　　　ans =  Min (  2*( dep[1]+dep[p]  )  + dep[1]*(n-1)  ,  dep[p]*(n-1) )     +  sum( 当前循环因子愤怒值和 ) - dep[p] 

　　将所有循环因子最优和累加 即为最终答案

解题代码

View Code

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include<algorithm>

using namespace std;

const int inf = 0x3fffffff;

const int N = 1e5+7;

typedef long long LL;

#define MIN(a,b) (a)<(b)?(a):(b)



int a[N], t[N], dep[N], n;

int sum, cnt, Min;

bool vis[N]; //用于标记位置

struct node{

    int x, id;

} p[N];



bool cmp_x( node a, node b)

{

    return a.x < b.x;

}

bool cmp_id(node a,node b)

{

    return a.id < b.id;

}

int check( int s ){

    sum = 0; cnt = 0; Min = inf;

    for(int i = s; i < n; i++)

        if( !vis[i] ) return i;

    return -1;

}

int main(){

    while( scanf("%d", &n) != EOF)

    {

        for(int i = 0; i < n; i++)

        {

            scanf("%d", &( p[i].x ) );

            p[i].id = i;

        }

        sort( p, p+n, cmp_x );    

        for(int i = 0; i < n; i++)

        {    

            a[ p[i].id ] = i; // 在 id 位置上的牛 编号为 i          

            dep[i] = p[i].x;  // 编号为i的牛,愤怒值    

        }        

        sort( p, p+n, cmp_id );    

        int pos = 0;

        LL ans = 0, tmp = dep[0];



        memset( vis, 0, sizeof(vis));    

        while( ( pos = check( pos ) ) != -1 ){

            int s = pos; // s位置    

            while( !vis[s] ){

                vis[s] = true;

                cnt++; sum += dep[ a[s] ]; //记录下s位置下 坐的编号为 a[s]的牛

                Min = MIN( Min, dep[ a[s] ] );

                s = a[s]; //查找 a[s]位置    

            }    

            if( cnt > 1 ){ //当前循环因子数量为cnt,其最小愤怒

                LL t1 =    1LL*(sum-Min)+1LL*Min*(cnt-1);

                LL t2 = 1LL*(sum-Min)+ 1LL*tmp*(cnt-1)+ 2*(tmp+Min);    

                ans += MIN( t1,t2 );    

            }        

            pos++;    

        }

        printf("%lld\n", ans);    

    }

    return 0;    

}