poj 3034 Whac-a-Mole 动态规划,线段上点个数

　　　dp（t,x,y） 表示 t时刻，锤子放到 (x,y) 点，打地鼠最高分

　　　状态方程：

　　　　　　dp（t, x, y） = Max { dp（t,x,y），dp（t-1,x1,y1）+ sum（x,y,x1,y1） } 

　　　其中  sqrt(  (x-x1)^2 + (y-y1)^2 ) <= d,     sum（x,y,x1,y1）表示 以 （x,y），（x1,y1）为端点的线段上 地鼠数量

　　

　　　对于 已知两端点 （x1,y1），（x2,y2）的线段，求其线段上 合法点个数，有多种方式：

　　　　　　一，  利用 直线方程来解，  若 x1==x2 或 y1 == y2  斜率不存在的特殊情况下，只需分别枚举 [y1,y2], [x1,x2]  （假定 y1 <= y2, x1 <= x2）

否则，则根据直线的方程来解: 

　　　　　　　

=>　　　　　　

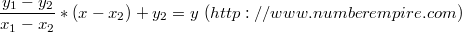
　　　若　　　   则 y 有整数解，  我们可以枚举 x, [ x1,x2]

 

　　　　　　二，  若 dx = | x1-x2 |, dy = | y1 - y2 | ,   d = Gcd（dx, dy）

　　　　　　　　  则 必有  

　　　　　　　　　　x1 + K*(dx/d)  = X2, 

　　　　　　　　　　y1 + K*(dy/d)  = Y2;      注意处理 dx , dy 都为0的情形

解题代码

View Code

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include<vector>

#include<math.h>

using namespace std;

#define MAX(a,b) (a)>(b)?(a):(b)

#define MIN(a,b) (a)<(b)?(a):(b)

int dp[11][50][50];

int vis[50][50];

int n, d, m;



vector< pair<int,int> > Q[15];



bool legal( int x, int y )

{

    if( (x>=-5) && (x<n+5) && (y>=-5) && (y<n+5) )

        return true;

    return false;

}

int sum( int x1, int y1, int x2, int y2 )

{

    int res = 0;    

    if( (x1 == x2) || (y1 == y2) )

    {

        if( x1 == x2 )

        {

            int s = MIN(y1,y2), t = MAX(y1,y2);     

            for(int y = s; y <= t; y++)    

                res += vis[x1+5][y+5];    

            return res;

        }

        else

        {

            int s = MIN(x1,x2), t = MAX(x1,x2);

            for(int x = s; x <= t; x++)

                res += vis[x+5][y1+5];

            return res;    

        }    

    }

    else

    {

        int s = MIN(x1,x2), t = MAX(x1,x2);    

        int ty = y1-y2, tx = x1-x2;

        for(int x = s; x <= t; x++)

        {

            int tmp = (x-x1)*ty;

            if( tmp%tx == 0 ){

                int y = tmp/tx + y1;

                res += vis[x+5][y+5];

            }

        }

        return res;    

    }

    return res;

}



// 增量求解两点间合法点数

int gcd(int a,int b){ return b==0?a:gcd(b,a%b); }

int getsum( int x1, int y1, int x2, int y2, int dx, int dy )

{

    int res = vis[x1+5][y1+5];

    do

    {

        x1 += dx;

        y1 += dy;

        res += vis[x1+5][y1+5];    

    }while( !(x1==x2&&y1==y2) );

    return res;

}

int main()

{

    while( scanf("%d%d%d", &n,&d,&m) != EOF)

    {

        if( n+d+m == 0 ) break;

        int x, y, t, maxt = 0;

        

        for(int i = 0; i <= 11; i++) Q[i].clear();

        for(int i = 0; i < m; i++)

        {

            scanf("%d%d%d",&x,&y,&t);

            Q[t].push_back( make_pair(x,y) );

            maxt = MAX( maxt, t );    

        }

        memset( vis, 0, sizeof(vis) );

        memset( dp, 0, sizeof(dp) );

    

        for( t = 1; t <= maxt; t++)

        {

            // 更新 t 时刻地鼠信息    

            memset( vis, 0, sizeof(vis) );

            for(int i = 0; i < Q[t].size(); i++)

                vis[ Q[t][i].first+5 ][ Q[t][i].second+5 ] = 1;

    

            // dp(t,x,y) t时,锤子在(x,y)位置，最高得分 

            for(x = -5; x < n+5; x++)

                for(y = -5; y < n+5; y++)

                {

                    // 枚举可由t-1时刻(x1,y1)位置状态得到

                    for(int dx = -d; dx <= d; dx++)

                        for(int dy = -d; dy <= d; dy++)

                        {

                            int x1 = x+dx, y1 = y+dy;

                            if( (legal(x1,y1) == false) || ( (int)ceil( sqrt(dx*dx+dy*dy) ) > d )  ) 

                                continue;

                            dp[t][x+5][y+5] = MAX(dp[t][x+5][y+5],dp[t-1][x1+5][y1+5]+sum(x,y,x1,y1) );    

                    /*  // 利用GCD增量法求解, 要特殊处理 公约数为0 的情况    

                            if( (dx==0) && (dy==0) ){

                                dp[t][x+5][y+5] = MAX( dp[t][x+5][y+5] ,dp[t-1][x+5][y+5]+vis[x+5][y+5] );    

                                continue;    

                            }    

                            int d = gcd( abs(dx),abs(dy));        

                            int tmp = getsum( x,y,x1,y1,dx/d,dy/d );    

                            dp[t][x+5][y+5] = MAX( dp[t][x+5][y+5], dp[t-1][x1+5][y1+5] + tmp );        

                    */    

                        }

                }

        }

        int ans = 0;

        for(int i = -5; i < n+5; i++)

            for(int j = -5; j < n+5; j++)

                ans = MAX( dp[maxt][i+5][j+5], ans );

        printf("%d\n", ans );    

    }

    return 0;

}