【matlab】分类回归——智能优化算法优化径向基神经网络
目录
径向基(Radial Basis Function, RBF)神经网络
一、基本概念
二、网络结构
三、工作原理
四、学习算法
五、优点与应用
六、与BP神经网络的比较
智能优化算法
常见的智能优化算法
灰狼优化算法(Grey Wolf Optimizer, GWO)
一、算法原理
二、算法流程
三、算法特点
四、应用场景
代码实现
定义目标函数
主函数
径向基(Radial Basis Function, RBF)神经网络
一、基本概念
径向基函数(RBF):是一个取值仅仅依赖于离原点(或某一中心点)距离的实值函数。在RBF神经网络中,最常用的径向基函数是高斯核函数,其形式为:
![]()
其中,x为核函数中心,σ为函数的宽度参数(或方差),控制了函数的径向作用范围。
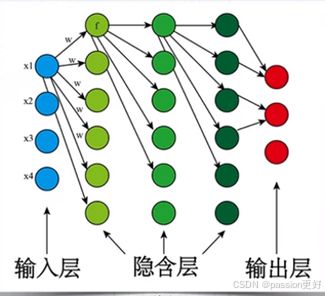
二、网络结构
RBF神经网络是一种三层神经网络,包括输入层、隐层和输出层。其结构特点如下:
- 输入层:仅起到输入数据的作用,与隐层之间的连接权值通常为1。
- 隐层:含有多个径向基神经元(激活函数为RBF),将低维非线性可分的输入映射到高维线性可分的空间。隐层节点的激活函数对输入局部响应,当输入靠近基函数中央范围时,隐层节点将产生较大的输出;远离中心点时,输出将呈指数衰减。
- 输出层:含有线性神经元(激活函数为线性函数),最终的输出是隐层神经元输出的线性加权和。
三、工作原理
RBF神经网络的基本思想是用RBF作为隐单元的“基”构成隐含层空间,将输入矢量直接映射到隐空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就确定了。隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和。网络的权可由线性方程组直接解出,从而大大加快学习速度并避免局部极小问题。
四、学习算法
RBF神经网络的学习问题主要是求解基函数的中心、方差以及隐含层到输出层的权值。常用的学习算法包括自组织选取中心学习方法,该方法分为无监督学习过程和有监督学习过程两个阶段:
- 无监督学习过程:求解隐含层基函数的中心与方差。通常使用K-means聚类算法确定RBF的中心,并根据各中心点之间的距离来确定隐节点的方差。
- 有监督学习过程:求解隐含层到输出层之间的权值。一般采用梯度下降法或最小二乘法等优化算法,通过训练样本集来获得满足监督要求的网络中心和其他权重参数。
五、优点与应用
RBF神经网络具有以下优点:
- 非线性拟合能力强:能够以任意精度逼近任意连续的非线性函数。
- 全局最优逼近:通过选择适当的中心点和宽度参数,可以实现全局最优逼近。
- 训练简洁、学习收敛速度快:由于隐层到输出层的映射是线性的,因此可以通过求解线性方程组直接得到权值,避免了复杂的迭代计算。
RBF神经网络已被广泛应用于函数逼近、语音识别、模式识别、图像处理、自动控制和故障诊断等领域。
六、与BP神经网络的比较
RBF神经网络与BP神经网络在结构和工作原理上存在一些差异:
- 逼近方式:BP神经网络是对非线性映射的全局逼近,而RBF神经网络是局部逼近。
- 网络结构:BP神经网络可以有多个隐含层,而RBF神经网络通常只有一个隐含层。
- 训练速度:由于RBF神经网络的隐层到输出层的映射是线性的,因此训练速度通常比BP神经网络快。
智能优化算法
智能优化算法通过模拟自然界或生物群体的某些行为规律,在搜索空间中寻找最优解或近似最优解。在优化RBF网络中,智能优化算法主要用于以下几个方面:
- 参数优化:包括隐含层神经元的中心位置、宽度以及输出层的权重等参数的优化。这些参数直接影响网络的映射能力和泛化性能。
- 结构优化:确定隐含层神经元的最佳数量。过多的神经元会增加计算复杂度,而过少的神经元则可能无法充分表示输入数据的特征。
常见的智能优化算法
在优化RBF网络中,常用的智能优化算法包括遗传算法、粒子群优化算法、蚁群算法等。这些算法各有特点,适用于不同的优化场景。
- 遗传算法:基于生物进化原理,通过选择、交叉和变异等操作来寻找最优解。遗传算法在优化RBF网络时,可以将网络的参数和结构编码为染色体,通过迭代进化来寻找最优的网络参数和结构。
- 粒子群优化算法:模拟鸟群或鱼群等生物群体的行为规律,通过粒子之间的信息共享和协作来寻找最优解。在优化RBF网络时,每个粒子可以代表一组网络参数,通过不断迭代更新粒子的位置和速度来寻找最优解。
- 蚁群算法:模拟蚂蚁觅食过程中的信息素传递机制,通过蚂蚁之间的信息素交流来寻找最优路径。虽然蚁群算法在优化RBF网络中的应用相对较少,但其启发式的搜索策略仍然具有一定的参考价值。
灰狼优化算法(Grey Wolf Optimizer, GWO)
一、算法原理
灰狼优化算法基于灰狼的社会等级和捕猎策略进行数学建模。灰狼群被分为四个等级:首领(Alpha, α)、副手(Beta, β)、侦察兵(Delta, δ)和欧米伽(Omega, ω)。算法通过模拟灰狼的社会合作行为来寻找最优解。
-
社会等级:在算法开始时,会随机生成一群灰狼(解的候选者),通过评估每个解的适应度来模拟社会等级。其中,最好的解被认为是Alpha(α),第二和第三好的解分别是Beta(β)和Delta(δ),其余的解则被视为Omega(ω)。这个社会结构帮助指导搜索过程,确保多样性和算法的收敛。
-
捕食行为:灰狼的捕食行为被简化为数学模型,用以指导灰狼(解的搜索代理)向猎物(最优解)靠近。这个过程涉及到“环绕猎物”、“追踪猎物”和“攻击猎物”三个阶段。
- 环绕猎物:通过数学公式模拟灰狼环绕猎物的行为,计算出灰狼应该在搜索空间中的位置,这个位置取决于当前的Alpha、Beta和Delta的位置。
- 追踪猎物:算法会根据猎物的动态位置更新灰狼的位置,以模拟追踪行为。
- 攻击猎物:当灰狼(搜索代理)足够接近最优解(猎物),算法会进行细微的调整,模拟攻击行为,以精确找到最优解。
二、算法流程
灰狼优化算法的一般流程如下:
-
生成初始群体:随机生成包含N个搜索代理(灰狼)的群体,每个灰狼代表解空间中的一个可能解。
-
初始化参数:设置算法的迭代次数、搜索代理的数量等。
-
评估适应度:计算每个搜索代理(灰狼)的适应度。
-
选择领导者:根据适应度,选择前三名最优秀的灰狼作为Alpha(最优解)、Beta(次优解)和Delta(第三优解)。
-
更新位置:根据Alpha、Beta和Delta的位置,更新每个Omega灰狼的位置。这个更新过程模拟了灰狼在狩猎过程中对猎物位置的估计和相应的移动。
-
迭代更新:重复上述步骤,直到满足停止条件(例如,达到最大迭代次数或达到足够好的解)。
三、算法特点
-
操作简单:灰狼优化算法具有相对简单的算法结构和较少的参数设置。
-
鲁棒性强:算法能够适应不同类型的优化问题,并在多种条件下保持稳定和适应性。
-
收敛速度快:由于灰狼算法在搜索过程中综合考虑了多个领导者(Alpha、Beta和Delta)的信息,它可以有效地平衡探索和开发的需求,从而加快收敛速度。
-
精确度较高:通过模拟灰狼的社会结构和狩猎行为,灰狼优化算法能够精确地找到问题的最优解或近似最优解。
四、应用场景
灰狼优化算法由于其独特的搜索机制和高效的全局探索能力,在多个领域都有广泛的应用。例如:
- 工程优化:在工程设计和建筑领域,灰狼算法被用来优化结构设计,如桥梁或建筑物的稳定性和耐久性。
- 能源管理:在能源行业,该算法用于优化电网的运行,如在可再生能源系统中平衡供需或优化电池存储系统的管理。
- 交通系统优化:灰狼算法可以应用于交通网络设计,如优化道路布局或交通信号灯的调度。
- 机器学习:在机器学习领域,灰狼算法被用来选择或优化特征,增强学习模型的准确性和效率。
- 调度问题:在制造业和物流领域,该算法用于优化生产线的调度,如确定最优的作业顺序或运输路线。
- 环境管理:灰狼算法还被用于环境科学领域,如优化水资源管理或评估环境影响。
代码示例
% Grey Wolf Optimizer
function [Alpha_score,Alpha_pos,Convergence_curve]=GWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
% Main loop
while lub;
Flag4lb=Positions(i,:)Alpha_score && fitnessAlpha_score && fitness>Beta_score && fitness 代码实现
智能优化算法优化RBF网络的过程通常包括以下几个步骤:
- 初始化:随机生成一组初始的网络参数和结构(如遗传算法中的初始种群)。
- 评价:使用训练数据集对当前的网络进行训练,并计算网络的性能指标(如均方误差)。
- 优化:根据智能优化算法的搜索策略,对当前的网络参数和结构进行调整(如遗传算法中的选择、交叉和变异操作)。
- 迭代:重复步骤2和步骤3,直到满足停止条件(如达到最大迭代次数或性能指标不再显著提高)。
- 输出:输出优化后的网络参数和结构,并使用测试数据集对优化后的网络进行验证。
定义目标函数
使用径向基函数(Radial Basis Function, RBF)神经网络来预测一组训练数据的输出,并通过交叉验证来评估模型的平均准确率,以此作为个体的适应度
function fitness = fobj(pop)
% 加载数据集和索引
p_train = evalin('base', 'P_train');
t_train = evalin('base', 'T_train');
% 提取最优参数
spread = pop(1);
% 初始化准确率数组
accuracies = zeros(1, size(p_train, 1));
% 进行交叉验证
cv = cvpartition(size(p_train, 1), 'KFold', 10);
for k = 1:cv.NumTestSets
% 创建 RBF 神经网络
net = newrbe(p_train, t_train, spread);
% 在测试集上进行预测
Y_train = sim(net, p_train);
% 数据反归一化
T_sim = vec2ind(Y_train);
T_true = vec2ind(t_train);
% 计算预测准确率
accuracy = sum(T_sim == T_true) / length(T_true);
% 保存准确率
accuracies(k) = accuracy;
end
% 计算平均准确率作为适应度
fitness = mean(accuracies);
end主函数
close all
clc
%% 读取数据集
% load data
%% 划分数据集
for ii=1:size(Tdata,2)
nanindex=isnan(Tdata(:,ii));
Tdata(nanindex,:)=[];
end
labels=Tdata(:,end); %classes
attributesData=Tdata(:,1:end-1); % data
[rows,colms]=size(attributesData); %size of data
[trainIdx,~,testIdx]=dividerand(rows,0.8,0,0.2);
P_train=attributesData(trainIdx,:); %training data
P_test=attributesData(testIdx,:); %testing data
T_train=labels(trainIdx); %training labels
T_test=labels(testIdx); %testing labels
%% 数据转置
P_train = P_train'; P_test = P_test';
T_train = T_train'; T_test = T_test';
%% 得到训练集和测试样本个数
M = size(P_train, 2);
N = size(P_test , 2);
% %% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input,0,1);
t_train = ind2vec(T_train);
t_test = ind2vec(T_test );
%% 灰狼优化算法参数设置
pop=20;%种群数量
maxiter=30;%迭代次数
c=0.1;%优化参数下限
d=1000;%优化参数上限
dim=1;%优化参数维度
fobj1 = @fobj;
%% 参数优化
[bestCVmse, Best_pos,Convergence_curve] =GWO(pop, maxiter,c,d,dim,fobj1);
%% 适应度曲线
figure
plot(1 : length(Convergence_curve), Convergence_curve, 'b-', 'LineWidth', 2);
title('DBO最佳适应度曲线', 'FontSize', 13);
xlabel('迭代次数', 'FontSize', 10);
ylabel('适应度', 'FontSize', 10);
xlim([1, length(Convergence_curve)])
grid on
%% 创建网络
spread = Best_pos;
net=newrbe(p_train, t_train, spread);
% 在测试集上进行预测
Y= sim(net,p_train);
Y1= sim(net, p_test);
T_sim1 = vec2ind(Y);
T_sim2 = vec2ind(Y1);
% 计算预测准确率
accuracy1 = sum((T_sim1 == T_train))/ M * 100;
accuracy2 = sum((T_sim2 == T_test))/ M * 100;
%% 打印结果
fprintf('精确度(训练集): %.2f%%\n', accuracy1);
fprintf('精确度(测试集): %.2f%%\n', accuracy2);