JavaScript 数据结构 ==== 二叉树
目录
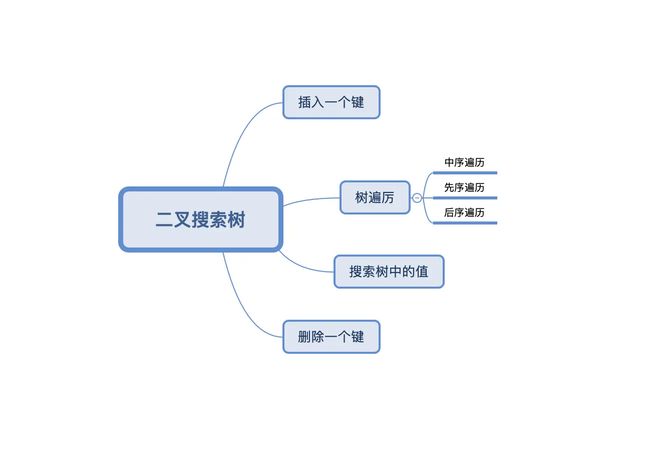
二叉树
结构
二叉树和二叉搜索树介绍
1.创建树
2.插入一个键
3.树的遍历
中序排序
先序遍历
后序遍历
4.搜索树中的值
5.删除节点
二叉树
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。 一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树,至少有2k-1个叶子节点,至多有2k-1个节点。。
- 以上是书面解答 —— 下面我总结一下
结构
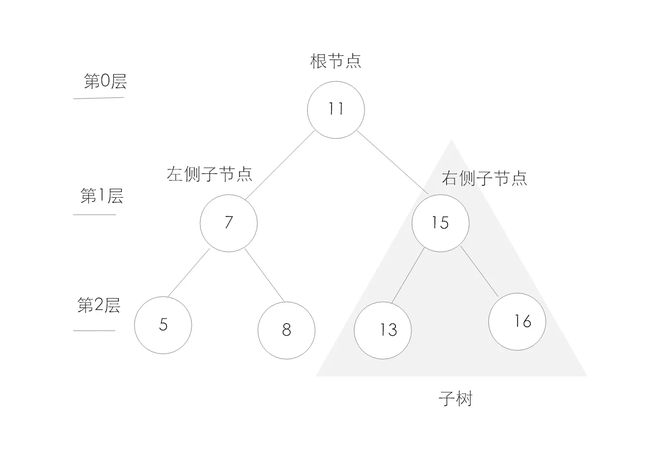
接下来让我们一起来探讨js数据结构中的树。这里的树类比现实生活中的树,有树干,树枝,在程序中树是一种数据结构,对于存储需要快速查找的数据非有用,它是一种分层数据的抽象模型。一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点以及零个或多个子节点。如下所以为一个树结构:)
和树相关的概念:1.子树:由节点和他的后代构成,如上图标示处。2.深度:节点的深度取决于它祖节点的数量,比如节点5有2个祖节点,他的深度为2。3.高度:树的高度取决于所有节点深度的最大值。
二叉树和二叉搜索树介绍
二叉树中的节点最多只能有2个子节点,一个是左侧子节点,一个是右侧子节点,这样定义的好处是有利于我们写出更高效的插入,查找,删除节点的算法。
二叉搜索树是二叉树的一种,但是它只允许你在左侧子节点存储比父节点小的值,但在右侧节点存储比父节点大的值。接下来我们将按照这个思路去实现一个二叉搜索树。
1.创建树
这里我们将使用构造函数去创建一个类:
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
class BST {
constructor(key) {
this.root = null;
}
}
- 我们将使用和链表类似的指针方式去表示节点之间的关系
- Node 类:这个类是二叉树中的节点,每个节点包含一个键(key)和两个指向其他节点的链接(left 和 right)。
- BST 类:这个类代表一个二叉搜索树,它有一个根节点
root。
2.插入一个键
向树中插入一个新的节点主要有以下三部分:
- 1.创建新节点的Node类实例
- 2.判断插入操作是否为根节点,是根节点就将其指向根节点
- 3.将节点加入非根节点的其他位置。
insert(key) {
if (this.root === null) {
this.root = new Node(key);
} else {
this.insertNode(this.root, key);
}
}- 首先,方法检查
key是否小于当前节点的key(即node.key)。 - 如果
key小于当前节点的key,则需要将新节点插入到当前节点的左子树中:- 如果当前节点的左子节点是
null(即没有左子节点),则创建一个新的Node实例,并将key作为其键值,然后将其赋值给node.left。 - 如果左子节点不是
null,则递归调用insertNode方法,将当前节点的左子节点作为新的node参数,继续在左子树中查找插入位置。
- 如果当前节点的左子节点是
- 如果
key大于或等于当前节点的key,则需要将新节点插入到当前节点的右子树中
insertNode(node, key) {
if (key < node.key) {
node.left === null
? (node.left = new Node(key))
: this.insertNode(node.left, key);
} else {
node.right === null
? (node.right = new Node(key))
: this.insertNode(node.right, key);
}
}3.树的遍历
访问树的所有节点有三种遍历方式:中序,先序和后序。
- 中序遍历:以从最小到最大的顺序访问所有节点
- 先序遍历:以优先于后代节点的顺序访问每个节点
- 后序遍历:先访问节点的后代节点再访问节点本身
根据以上的介绍,我们可以有以下的实现代码。
中序排序
中序遍历是一种按升序访问树中所有节点的遍历方法。在二叉树中,中序遍历的顺序是先访问左子树,然后访问根节点,最后访问右子树。这种遍历方式对于二叉搜索树(BST)特别有用,因为它可以保证遍历的结果是树中元素的有序列表。
中序遍历的步骤:
- 访问左子树,进行中序遍历。
- 访问根节点。
- 访问右子树,进行中序遍历。
- 代码实现
inOrderTraverse(cb) {
this.inOrderTraverseNode(this.root, cb);
}
// 辅助函数
inOrderTraverseNode(node, cb) {
if (node !== null) {
this.inOrderTraverseNode(node.left, cb);
cb(node.key);
this.inOrderTraverseNode(node.right, cb);
}
}递归的调用过程是不断往左边走,当左边走不下去了,就打印节点,并转向右边,然后右边继续这个过程。
我们在迭代实现时,就可以用栈来模拟上面的调用过程。
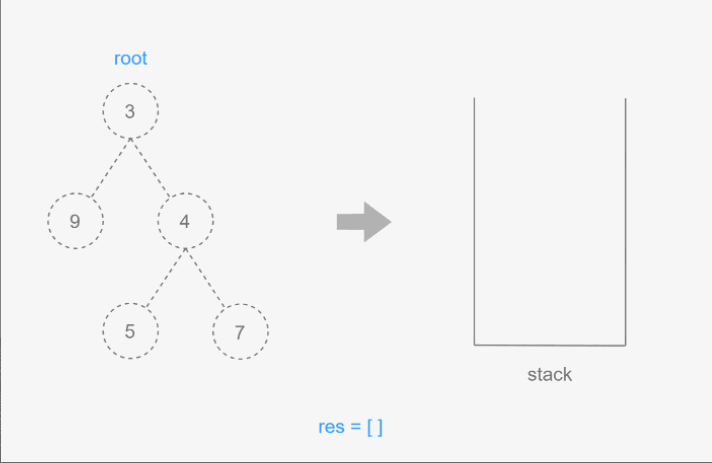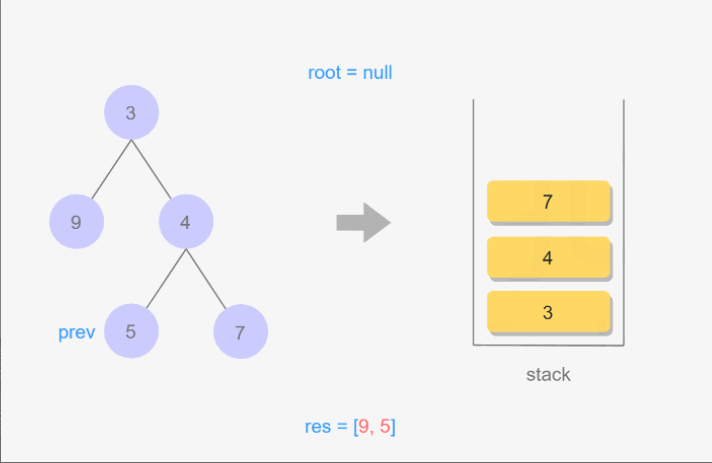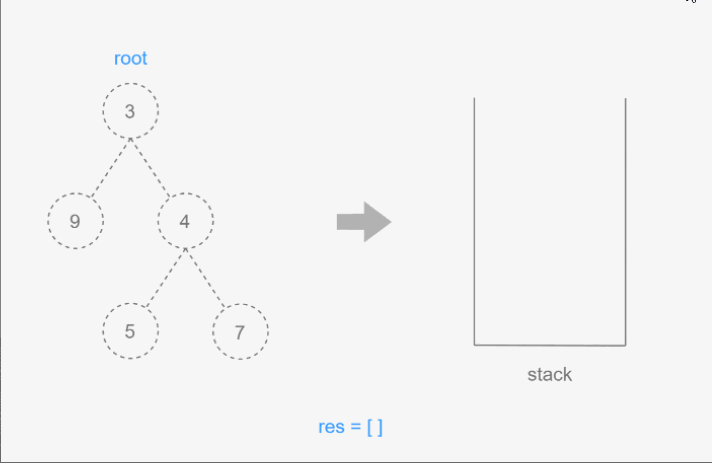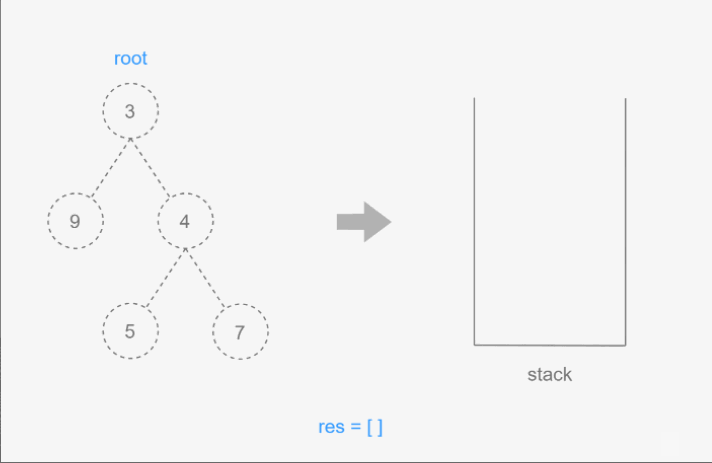
先序遍历
递归思路:先树根,然后左子树,然后右子树。每棵子树递归。在迭代算法中,思路演变成,每到一个节点 A,就应该立即访问它。 因为,每棵子树都先访问其根节点。对节点的左右子树来说,也一定是先访问根。 在 A 的两棵子树中,遍历完左子树后,再遍历右子树。
因此,在访问完根节点后,遍历左子树前,要将右子树压入栈。
先序遍历的步骤:
- 访问根节点。
- 访问左子树,进行先序遍历。
- 访问右子树,进行先序遍历。
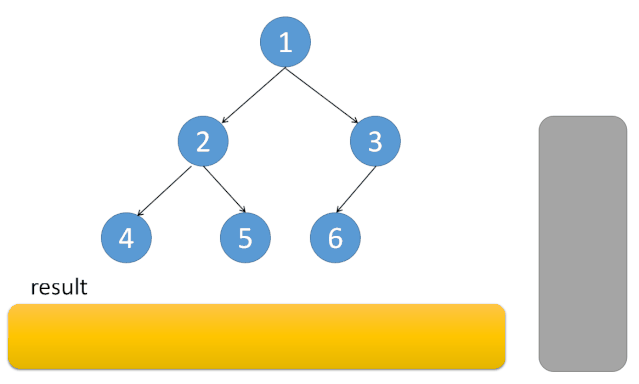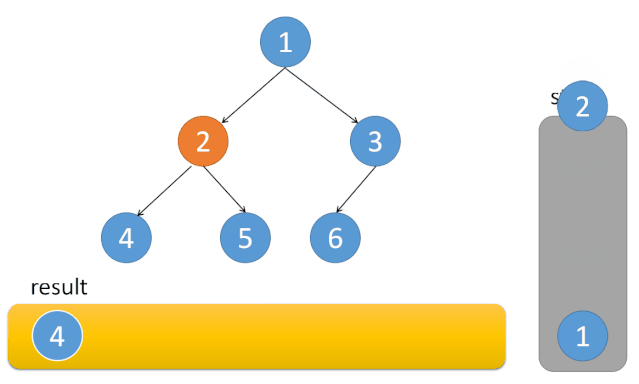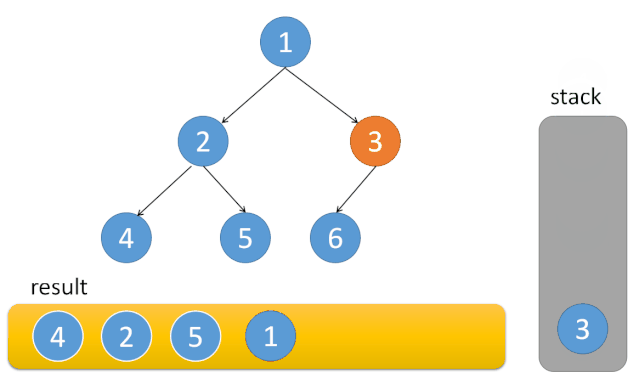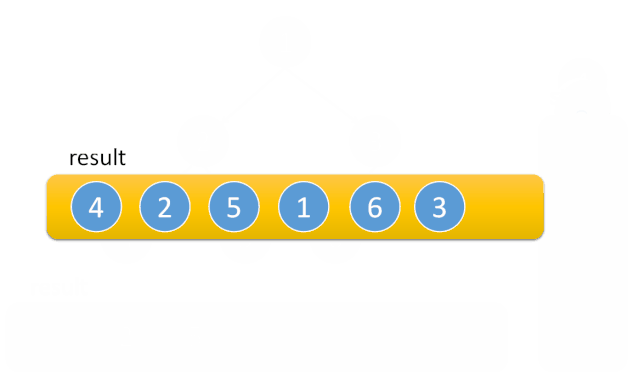
后序遍历
后序遍历是一种先访问所有子节点,最后访问当前节点的遍历方法。在后序遍历中,根节点是最后被访问的,遍历顺序是左子树、右子树,然后是根节点。
后序遍历的步骤:
- 访问左子树,进行后序遍历。
- 访问右子树,进行后序遍历。
- 访问根节点。
// 后续遍历 --- 先访问后代节点,再访问节点本身
postOrderTraverse(cb) {
this.postOrderTraverseNode(this.root, cb);
}
// 后续遍历辅助方法
postOrderTraverseNode(node, cb) {
if (node !== null) {
this.postOrderTraverseNode(node.left, cb);
this.postOrderTraverseNode(node.right, cb);
cb(node.key);
}
}
4.搜索树中的值
在树中有三种经常执行的搜索类型:最大值,最小值,特定的值。
- 每个节点的左子树上所有节点的键值都小于它的键值。
- 每个节点的右子树上所有节点的键值都大于它的键值。
- 每个节点的左、右子树也分别是二叉搜索树。
代码中的几个方法分别实现了以下功能:
-
min()和minNode(node):这两个方法用于找到二叉搜索树中的最小值。最小值是树中左子树的最末端节点的键值。minNode方法从给定的节点开始,一直向左遍历,直到找到最左端的节点,然后返回该节点的键值。 -
max()和maxNode(node):这两个方法用于找到二叉搜索树中的最大值。最大值是树中右子树的最末端节点的键值。maxNode方法从给定的节点开始,一直向右遍历,直到找到最右端的节点,然后返回该节点的键值。 -
search(key)和searchNode(node, key):这两个方法用于在二叉搜索树中搜索一个特定的键值。searchNode方法从给定的节点开始,根据键值的大小递归地在左子树或右子树中搜索,直到找到匹配的键值或遍历到空节点,表示键值不存在于树中。
具体到搜索值的过程,searchNode 方法的工作原理如下:
- 如果当前节点为
null,表示已经到达树的末端,但没有找到键值,返回false。 - 如果键值小于当前节点的键值,递归地在当前节点的左子树中搜索。
- 如果键值大于当前节点的键值,递归地在当前节点的右子树中搜索。
- 如果键值等于当前节点的键值,表示找到了匹配的键值,返回
true。
这种搜索方法利用了二叉搜索树的性质,可以高效地进行查找操作,其时间复杂度通常为 O(h),其中 h 是树的高度。在平衡的二叉搜索树中,这个操作的时间复杂度接近 O(log n),其中 n 是树中节点的数量。
// 最小值;
min() {
return this.minNode(this.root);
}
minNode(node) {
if (node) {
while (node && node.left !== null) {
node = node.left;
}
return node.key;
}
return null;
}
// 最大值;
max() {
return this.maxNode(this.root);
}
maxNode(node) {
if (node) {
while (node && node.right !== null) {
node = node.right;
}
return node.key;
}
return null;
}
// 搜索树中某个值
search(key) {
return this.searchNode(this.root, key);
}
// 搜索辅助方法
searchNode(node, key) {
if (node === null) {
return false;
}
if (key < node.key) {
return this.searchNode(node.left, key);
} else if (key > node.key) {
return this.searchNode(node.right, key);
} else {
return true;
}
}5.删除节点
![]()
删除二叉搜索树中的一个节点通常分为以下几个步骤:
-
查找要删除的节点:首先,需要找到要删除的节点。这可以通过递归遍历树来完成。
-
确定删除情况:找到节点后,需要确定该节点是叶子节点、只有一个子节点的节点,还是有两个子节点的节点。
-
删除叶子节点:如果节点是叶子节点(即没有子节点),可以直接删除该节点。
-
删除只有一个子节点的节点:如果节点只有一个子节点,可以删除该节点,并用其子节点来替代它。
-
删除有两个子节点的节点:这是最复杂的情况。如果节点有两个子节点,不能简单地删除它,因为这会破坏二叉搜索树的性质。通常的做法是找到该节点的直接前驱(通常是其右子树中的最小节点)或直接后继(通常是其左子树中的最大节点),然后将其值复制到当前节点上,接着删除原来的直接前驱或直接后继。
// 删除
remove(key) {
this.root = this.removeNode(this.root, key);
}
findMinNode(node) {
if (node) {
while (node && node.left !== null) {
node = node.left;
}
return node;
}
return null;
}
removeNode(node, key) {
if (node === null) {
return null;
}
if (key < node.key) {
node.left = this.removeNode(node.left, key);
return node;
} else if (key > node.key) {
node.right = this.removeNode(node.right, key);
return node;
} else {
if (node.left === null && node.right === null) {
node = null;
return node;
}
if (node.left === null) {
node = node.right;
return node;
} else if (node.right === null) {
node = node.left;
return node;
}
// 有两个子节点的节点
let aux = this.findMinNode(node.right);
node.key = aux.key;
node.right = this.removeNode(node.right, aux.key);
return node;
}
}remove 方法是删除操作的入口,它调用 removeNode 方法来递归地删除节点。findMinNode 方法用于找到给定节点的右子树中的最小节点,这个最小节点将被用来替换当前要删除的节点。
以下是 removeNode 方法的逻辑解释:
- 如果当前节点为空,说明没有找到要删除的节点,直接返回
null。 - 如果要删除的键值小于当前节点的键值,说明要删除的节点在当前节点的左子树中,递归地在左子树中删除。
- 如果要删除的键值大于当前节点的键值,说明要删除的节点在当前节点的右子树中,递归地在右子树中删除。
- 如果找到了要删除的节点(键值相等),则根据其子节点的数量来决定删除策略:
- 如果没有子节点,直接删除该节点。
- 如果只有一个子节点(左或右),用其子节点替换当前节点。
- 如果有两个子节点,找到右子树中的最小节点,用该最小节点的键值替换当前节点的键值,然后删除原来的最小节点。
通过这种方式,二叉搜索树在删除节点后仍然保持其性质,即任何节点的左子树上的键值都小于该节点的键值,右子树上的键值都大于或等于该节点的键值。