Day54 | Floyd 算法 A * 算法

语言

Java

Floyd 算法

题目

97. 小明逛公园

97. 小明逛公园

题目描述

小明喜欢去公园散步，公园内布置了许多的景点，相互之间通过小路连接，小明希望在观看景点的同时，能够节省体力，走最短的路径。 

给定一个公园景点图，图中有 N 个景点（编号为 1 到 N），以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。

小明有 Q 个观景计划，每个计划都有一个起点 start 和一个终点 end，表示他想从景点 start 前往景点 end。由于小明希望节省体力，他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。

输入描述

第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。 

接下来的 M 行，每行包含三个整数 u, v, w，表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。 

接下里的一行包含一个整数 Q，表示观景计划的数量。 

接下来的 Q 行，每行包含两个整数 start, end，表示一个观景计划的起点和终点。

输出描述

对于每个观景计划，输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径，则输出 -1。

思路

1. 初始化：创建一个二维数组（在 Java 中为 int[][]）表示图的邻接矩阵。由于图中的边可能不存在，所以对于不存在的边，初始化为一个大数（在这个例子中是 10005），表示无穷大。
2. 读取输入：从标准输入读取图的顶点数 n 和边的数量 m，然后读取每条边的两个端点以及边的权重，并更新邻接矩阵中的相应位置。
3. Floyd-Warshall 算法：该算法通过考虑每个顶点作为中间点的可能性来动态更新所有顶点对之间的最短路径。它的时间复杂度是 O(n^3)，其中 n 是顶点的数量。
4. 处理查询：读取查询的数量 z，然后对于每个查询读取起始点 start 和终点 end，并输出这两点之间的最短路径长度。如果两点间没有路径，则输出 -1。

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();

        int[][] grid = new int[n + 1][n + 1];
        for (int[] row : grid) {
            java.util.Arrays.fill(row, 10005);  // 因为边的最大距离是10^4
        }

        for (int i = 0; i < m; i++) {
            int p1 = scanner.nextInt();
            int p2 = scanner.nextInt();
            int val = scanner.nextInt();
            grid[p1][p2] = val;
            grid[p2][p1] = val; // 注意这里是双向图
        }

        // 开始 floyd
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    if (grid[i][k] != 10005 && grid[k][j] != 10005)
                        grid[i][j] = Math.min(grid[i][j], grid[i][k] + grid[k][j]);
                }
            }
        }

        // 输出结果
        int z = scanner.nextInt();
        while (z-- > 0) {
            int start = scanner.nextInt();
            int end = scanner.nextInt();
            if (grid[start][end] == 10005)
                System.out.println(-1);
            else
                System.out.println(grid[start][end]);
        }
    }
}

易错点

在更新路径时，必须检查是否真的通过中间点 k 可以得到更短的路径。在 Java 版本中，我添加了一个检查 if (grid[i][k] != 10005 && grid[k][j] != 10005) 来确保不会尝试通过一个不存在的路径来更新距离。

A * 算法

127. 骑士的攻击

题目

127. 骑士的攻击

题目描述

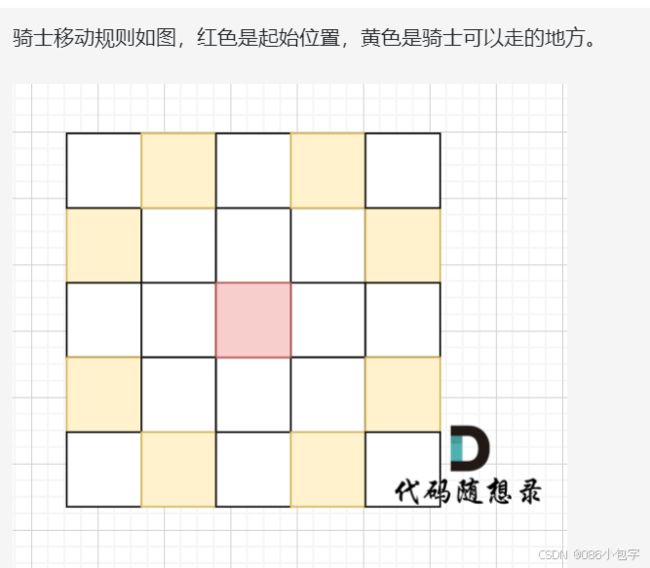
在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量，1 <= n <= 100。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

思路

1. 初始化：

   • 创建一个 moves 数组来记录从起点到各个点的最短步数。
   • 创建一个 dir 数组来表示骑士的八个可能移动方向。
   • 初始化 moves 数组为 0 表示尚未探索过。

2. 创建骑士对象：

   • 定义一个 Knight 类来表示骑士的状态，包括当前位置（x, y）和 G、H、F 值。

3. 启发式函数：

   • 使用欧几里得距离的平方（不计算开方）作为启发式函数 H，因为计算平方根会增加计算成本，而且在比较时不需要精确的欧几里得距离。

4. A 算法*：

   • 将起点加入优先队列中。
   • 在队列非空的情况下，重复以下步骤：
     • 取出队列中的当前节点。
     • 如果当前节点是终点，则停止搜索。
     • 否则，遍历当前节点的所有可能的移动方向，并更新 moves 数组。
     • 计算新节点的 G、H、F 值，并将其加入队列。

5. 输出结果：

   • 输出从起点到终点的最短步数。

代码

import java.util.PriorityQueue;
import java.util.Scanner;

public class Main {

    private static final int MAX_SIZE = 1000;
    private static int moves[][] = new int[MAX_SIZE + 1][MAX_SIZE + 1];
    private static int dir[][] = {{-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}};
    private static int b1, b2;

    static class Knight implements Comparable {
        int x, y;
        int g, h, f;

        public Knight(int x, int y, int g, int h, int f) {
            this.x = x;
            this.y = y;
            this.g = g;
            this.h = h;
            this.f = f;
        }

        @Override
        public int compareTo(Knight k) {
            return this.f - k.f;
        }
    }

    private static int heuristic(Knight k) {
        return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 欧拉距离
    }

    private static void aStar(Knight k) {
        PriorityQueue queue = new PriorityQueue<>();
        queue.add(k);

        while (!queue.isEmpty()) {
            Knight cur = queue.poll();
            if (cur.x == b1 && cur.y == b2) {
                break;
            }
            for (int i = 0; i < 8; i++) {
                Knight next = new Knight(0, 0, 0, 0, 0);
                next.x = cur.x + dir[i][0];
                next.y = cur.y + dir[i][1];
                if (next.x < 1 || next.x > MAX_SIZE || next.y < 1 || next.y > MAX_SIZE) {
                    continue;
                }
                if (moves[next.x][next.y] == 0) {
                    moves[next.x][next.y] = moves[cur.x][cur.y] + 1;

                    // 开始计算 F
                    next.g = cur.g + 5; // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
                    next.h = heuristic(next);
                    next.f = next.g + next.h;
                    queue.add(next);
                }
            }
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        while (n-- > 0) {
            int a1 = scanner.nextInt();
            int a2 = scanner.nextInt();
            b1 = scanner.nextInt();
            b2 = scanner.nextInt();

            for (int i = 1; i <= MAX_SIZE; i++) {
                java.util.Arrays.fill(moves[i], 0);
            }

            Knight start = new Knight(a1, a2, 0, heuristic(new Knight(a1, a2, 0, 0, 0)), 0);
            aStar(start);

            System.out.println(moves[b1][b2]);
        }
        scanner.close();
    }
}

易错点

数组边界检查：确保骑士的移动不会超出棋盘范围。

优先队列：使用最小堆来保证每次取出的节点是最优的（即 F 值最小）。

清除状态：每次处理完一个测试用例后，需要清除 moves 数组和优先队列的状态，以便处理下一个测试用例。

总结

继续加油！

奋斗以求改善生活，是可敬的行为。