Day64:Floyd 算法 A * 算法 小明逛公园 和骑士的攻击

97. 小明逛公园

题目描述

小明喜欢去公园散步，公园内布置了许多的景点，相互之间通过小路连接，小明希望在观看景点的同时，能够节省体力，走最短的路径。 

给定一个公园景点图，图中有 N 个景点（编号为 1 到 N），以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。

小明有 Q 个观景计划，每个计划都有一个起点 start 和一个终点 end，表示他想从景点 start 前往景点 end。由于小明希望节省体力，他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。

输入描述

第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。 

接下来的 M 行，每行包含三个整数 u, v, w，表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。 

接下里的一行包含一个整数 Q，表示观景计划的数量。 

接下来的 Q 行，每行包含两个整数 start, end，表示一个观景计划的起点和终点。

输出描述

对于每个观景计划，输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径，则输出 -1。

输入示例

7 3
2 3 4
3 6 6
4 7 8
2
2 3
3 4

输出示例

4
-1

提示信息

从 2 到 3 的路径长度为 4，3 到 4 之间并没有道路。

1 <= N, M, Q <= 1000.

思路:

本题是多源最短路，即 求多个起点到多个终点的多条最短路径

最短路算法-Floyd 算法

Floyd 算法对边的权值正负没有要求，都可以处理。

1、确定dp数组（dp table）以及下标的含义

这里我们用 grid数组来存图，那就把dp数组命名为 grid。

grid[i][j][k] = m，表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m

2、确定递推公式

在上面的分析中我们已经初步感受到了递推的关系。

我们分两种情况：

1. 节点i 到 节点j 的最短路径经过节点k
2. 节点i 到 节点j 的最短路径不经过节点k

对于第一种情况，grid[i][j][k] = grid[i][k][k - 1] + grid[k][j][k - 1]

节点i 到 节点k 的最短距离 是不经过节点k，中间节点集合为[1...k-1]，所以 表示为grid[i][k][k - 1]

节点k 到 节点j 的最短距离 也是不经过节点k，中间节点集合为[1...k-1]，所以表示为 grid[k][j][k - 1]

第二种情况，grid[i][j][k] = grid[i][j][k - 1]

如果节点i 到 节点j的最短距离 不经过节点k，那么 中间节点集合[1...k-1]，表示为 grid[i][j][k - 1]

因为我们是求最短路，对于这两种情况自然是取最小值。

即： grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1]， grid[i][j][k - 1])

3、dp数组如何初始化

grid[i][j][k] = m，表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m。

刚开始初始化k 是不确定的。

例如题目中只是输入边（节点2 -> 节点6，权值为3），那么grid[2][6][k] = 3，k需要填什么呢？

把k 填成1，那如何上来就知道 节点2 经过节点1 到达节点6的最短距离是多少 呢。

所以 只能 把k 赋值为 0，本题 节点0 是无意义的，节点是从1 到 n。

grid数组中其他元素数值应该初始化多少呢？

本题求的是最小值，所以输入数据没有涉及到的节点的情况都应该初始为一个最大数。

4、确定遍历顺序

从递推公式：grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1]， grid[i][j][k - 1]) 可以看出，我们需要三个for循环，分别遍历i，j 和k

而 k 依赖于 k - 1， i 和j 的到 并不依赖与 i - 1 或者 j - 1 等等。

 k 放在最外层,至于遍历 i 和 j 的话，for 循环的先后顺序无所谓。

代码参考:

import java.util.*;

public class Main {

    public static void main(String[] args) {
        int n, m;
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        int[][][] grid = new int[n + 1][n + 1][n + 1];
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n;j++){
                Arrays.fill(grid[i][j],1001);
            }
        }
        while (m-- > 0) {
            int x = in.nextInt();
            int y = in.nextInt();
            int val=in.nextInt();
            grid[x][y][0] = val;
            grid[y][x][0] = val;//双向图
        }
        // 开始 floyd
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    grid[i][j][k] = Math.min(grid[i][j][k - 1], grid[i][k][k - 1] + grid[k][j][k - 1]);
                }
            }
        }
        int q = in.nextInt();
        while (q-- > 0) {
            int start = in.nextInt();
            int end = in.nextInt();
            System.out.println(grid[start][end][n] == 1001 ? -1 : grid[start][end][n]);
        }
    }
}

空间优化

floyd算法的时间复杂度相对较高，适合 稠密图且源点较多的情况。

import java.util.*;

public class Main {

    public static void main(String[] args) {
        int n, m;
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        m = in.nextInt();
        int[][] grid = new int[n + 1][n + 1];
        for(int i=0;i<=n;i++){
                Arrays.fill(grid[i],1001);
        }
        while (m-- > 0) {
            int x = in.nextInt();
            int y = in.nextInt();
            int val=in.nextInt();
            grid[x][y] = val;
            grid[y][x] = val;//双向图
        }
        // 开始 floyd
        for (int k = 1; k <= n; k++) {
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= n; j++) {
                    grid[i][j] = Math.min(grid[i][j], grid[i][k]+ grid[k][j]);
                }
            }
        }
        int q = in.nextInt();
        while (q-- > 0) {
            int start = in.nextInt();
            int end = in.nextInt();
            System.out.println(grid[start][end] == 1001 ? -1 : grid[start][end]);
        }
    }
}

---

127. 骑士的攻击

题目描述

在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量，1 <= n <= 100。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

输入示例

6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6

输出示例

2
4
6
5
1
0

提示信息

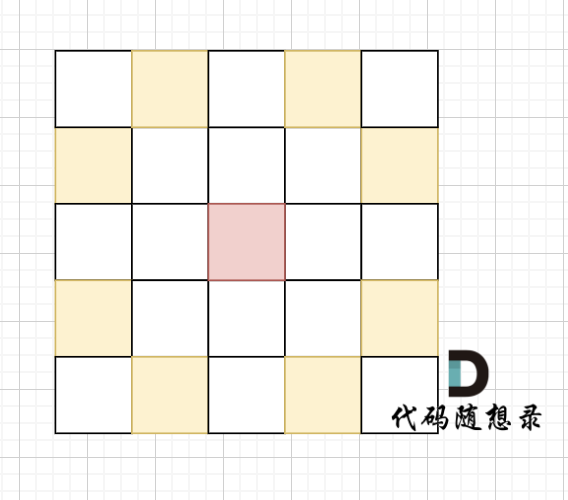
骑士移动规则如图，红色是起始位置，黄色是骑士可以走的地方。

思路:使用A*算法

 A * 是有方向性的去搜索,

那么 A * 为什么可以有方向性的去搜索，它的如何知道方向呢？

其关键在于 启发式函数。

从队列里取出什么元素，接下来就是从哪里开始搜索。

所以 启发式函数 要影响的就是队列里元素的排序！

这是影响BFS搜索方向的关键。

对队列里节点进行排序，就需要给每一个节点权值，如何计算权值呢？

每个节点的权值为F，给出公式为：F = G + H

G：起点达到目前遍历节点的距离

F：目前遍历的节点到达终点的距离

本题的图是无权网格状，在计算两点距离通常有如下三种计算方式：

1. 曼哈顿距离，计算方式： d = abs(x1-x2)+abs(y1-y2)
2. 欧氏距离（欧拉距离） ，计算方式：d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
3. 切比雪夫距离，计算方式：d = max(abs(x1 - x2), abs(y1 - y2))

选择哪一种距离计算方式 也会导致 A * 算法的结果不同。

本题，采用欧拉距离才能最大程度体现 点与点之间的距离。

A * 算法 并不是一个明确的最短路算法，A * 算法搜的路径如何，完全取决于 启发式函数怎么写。

A * 算法并不能保证一定是最短路，因为在设计 启发式函数的时候，要考虑 时间效率与准确度之间的一个权衡。

保证运行效率的情况下，A * 算法中的启发式函数 设计往往不是最短路，而是接近最短路的 次短路设计。 

import java.time.format.SignStyle;
import java.util.*;

public class Main {
    static int[][] moves = new int[1001][1001];
    static int[][] dir = {{-2, -1}, {-2, 1}, {-1, 2}, {1, 2}, {2, 1}, {2, -1}, {1, -2}, {-1, -2}};
    static int startX, startY, endX, endY;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        while (n-- > 0) {
            for (int i = 0; i <= 1000; i++) {
                Arrays.fill(moves[i], 0);
            }
            startX = in.nextInt();
            startY = in.nextInt();
            endX = in.nextInt();
            endY = in.nextInt();
            Node node = new Node(startX, startY);
            int H = Heuristic(node, endX, endY);
            node.setG(0);
            node.setH(H);
            node.setF();
            astar(node);
            System.out.println(moves[endX][endY]);
        }
    }

    public static void astar(Node start) {

        Node next, cur;
        PriorityQueue queue = new PriorityQueue<>(new Comparator() {
            @Override
            public int compare(Node o1, Node o2) {
                return o1.getF()-o2.getF();
            }
        });
        queue.add(start);
        while (!queue.isEmpty()) {
            cur = queue.poll();
            if (cur.getX() == endX && cur.getY() == endY) {
                break;
            }
            for (int i = 0; i < 8; i++) {
                int nextx = cur.getX() + dir[i][0];
                int nexty = cur.getY() + dir[i][1];
                if (nexty > 1000 || nexty < 1 || nextx > 1000 || nextx < 1) {
                    continue;
                }
                if (moves[nextx][nexty] == 0) {
                    next = new Node(nextx, nexty);
                    moves[next.x][next.y] = moves[cur.x][cur.y] + 1;
                    // 开始计算F
                    next.setG(cur.getG() + 5); // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
                    next.setH(Heuristic(next, endX, endY));
                    next.setF();
                    queue.add(next);
                  

                }
            }
        }

    }

    public static int Heuristic(Node node, int endX, int endY) {
        return (node.getX() - endX) * (node.getX() - endX) + (node.getY() - endY) * (node.getY() - endY);
    }

}

class Node {
    int x;
    int y;
    int g, h, f;

    //F = G + H
    public Node(int x, int y) {
        this.x = x;
        this.y = y;
    }

    public void setG(int g) {
        this.g = g;
    }

    public void setH(int h) {
        this.h = h;
    }

    public void setF() {
        this.f = this.g + this.h;
    }

    public int getX() {
        return x;
    }

    public int getY() {
        return y;
    }

    public int getG() {
        return g;
    }

    public int getH() {
        return h;
    }

    public int getF() {
        return f;
    }

    @Override
    public String toString() {
        return "Node{" +
                "x=" + x +
                ", y=" + y +
                ", f=" + f +
                '}';
    }
}