每日刷题(图论)
P1119 灾后重建
P1119 灾后重建 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
看数据范围知道需要用到Floyd算法,但是道路是不能直接用的,需要等到连接道路的两个村庄重建好才可以使用,所以这需要按照时间依次加入中转点,再更新dis数组。
代码
#include
#define int long long
#define TEST int T; cin >> T; while (T--)
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
const int N = 1e6 + 30;
const int M = 1e3 + 10;
const int inf = 512785182741247112;
const int mod = 100003;
using namespace std;
int f[201][201];
int n, m;
int a[201];
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
f[i][j] = inf;
}
}
for (int i = 0; i < m; i++)
{
int x, y, z;
cin >> x >> y >> z;
f[x][y] = f[y][x] = z;
}
int q;
cin >> q;
int now = 0;
for (int i = 0; i < q; i++)
{
int x, y, t;
cin >> x >> y >> t;
if (a[x] > t || a[y] > t)
{
cout << "-1\n";
continue;
}
while (a[now] <= t&&now P6464 [传智杯 #2 决赛] 传送门
P6464 [传智杯 #2 决赛] 传送门 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
这道题需要我们使用Floyd算法,因为计算全源最短路径需要三层循环,但是没完枚举传送门的建设也需要两重循环,五重循环必定超时,所以我们需要将它优化成四重循环,我们发现建设传送门时只对以传送门建设点为中转点的边有影响,所以我们可以优化为四重循环。
代码
#include
#define inf 1234567890
using namespace std;
int n,m,mp1[120][120],mp2[120][120],ans=inf;
void back()//返回原图
{
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
mp2[i][j]=mp1[i][j];
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
mp1[i][j]=inf;
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
mp1[x][y]=mp1[y][x]=z;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
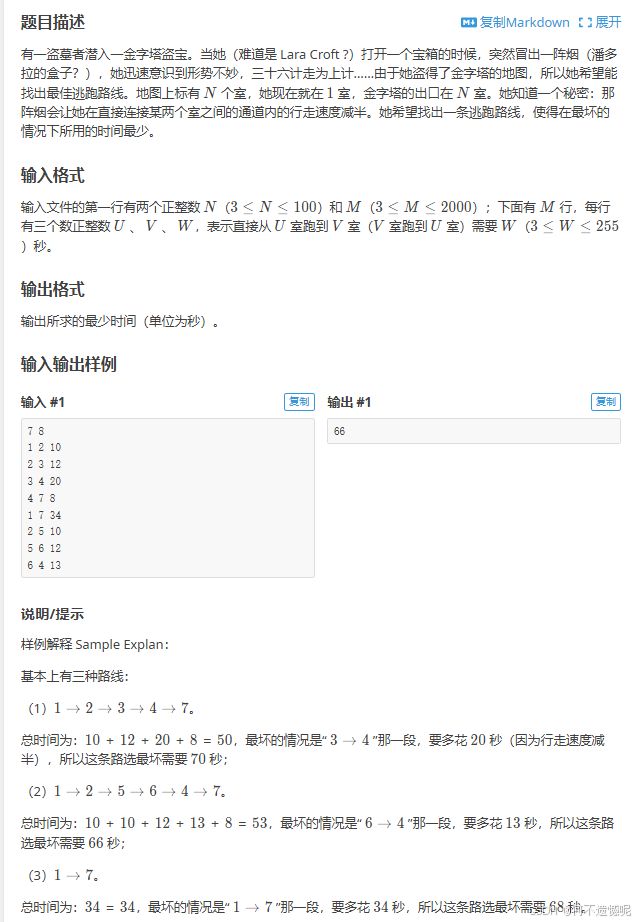
if(mp1[i][k] P2349 金字塔
P2349 金字塔 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
思路
最短路模板题,但是需要维护最大值,一开始我将答案全部储存在dis数组里面,结果只得40分
int n, m, head[N], cnt;
int mxx[N];
struct node
{
int u, v, w;
}e[N];
void add(int x, int y, int z) {
e[++cnt].u = y;
e[cnt].w = z;
e[cnt].v = head[x];
head[x] = cnt;
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
add(y, x, z);
}
vectordis(n + 1, inf);
dis[1] = 0;
priority_queueq;
q.emplace(0, 1);
while (q.size()) {
auto it = q.top();
q.pop();
int x = it.second;
for (int i = head[x]; i; i = e[i].v) {
int now = e[i].u;
mxx[now] = max(mxx[x], e[i].w);
if (dis[now] > e[i].w + dis[x] + mxx[now] - mxx[x]) {
dis[now] = e[i].w + dis[x] + mxx[now] - mxx[x];
q.emplace(-dis[now], now);
}
}
}
cout << dis[n] << '\n';
} 所以我们需要用两个数组来维护答案最小值,dis数组和维护的边权最大值,下面是AC代码。
代码
#define _CRT_SECURE_NO_WARNINGS
#include
#include
#define int long long
#define pb push_back
#define TEST int T; cin >> T; while (T--)
#define ios ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr)
#define lowbit(x) x&(-x)
#define pll pair
const int N = 3e5 + 30;
const int M = 1e3 + 10;
const int inf = 512785182741247112;
const int mod = 1e9 + 7;
using namespace std;
int n, m, head[N], cnt;
int mxx[N];
struct node
{
int u, v, w;
}e[N];
void add(int x, int y, int z) {
e[++cnt].u = y;
e[cnt].w = z;
e[cnt].v = head[x];
head[x] = cnt;
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
add(y, x, z);
}
vectordis(n + 1, inf);
dis[1] = 0;
priority_queueq;
q.emplace(0, 1);
while (q.size()) {
auto it = q.top();
q.pop();
int x = it.second;
for (int i = head[x]; i; i = e[i].v) {
int now = e[i].u;
if (dis[now] +mxx[now]> e[i].w + dis[x] + max(e[i].w,mxx[x])) {
mxx[now] = max(e[i].w, mxx[x]);
dis[now] = e[i].w + dis[x];
q.emplace(-(dis[now]+mxx[now]), now);
}
}
}
cout << dis[n]+mxx[n] << '\n';
}
signed main() {
ios;
solve();
return 0;
}