线性代数——特征值与特征向量的性质
(1)设A为方阵,则A与 A T A^{T} AT有相同的特征值。
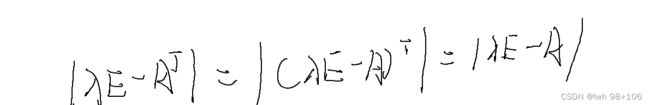
此处用到了两个关键性质,一:单位阵的转置为其本身,二:转置并不改变行列式的值。
(2):
设n阶方阵A=( a i j a_{ij} aij)的n个特征值为 λ 1 \lambda_{1} λ1, λ 2 \lambda_{2} λ2,… λ n \lambda_{n} λn,则 λ 1 + λ 2 + λ 3 + . . . λ n = a 11 + a 22 + a 33 + . . . + a n n \lambda_{1}+\lambda_{2}+\lambda_{3}+...\lambda_{n}=a_{11}+a_{22}+a_{33}+...+a_{nn} λ1+λ2+λ3+...λn=a11+a22+a33+...+ann
(2) λ 1 ∗ λ 2 ∗ λ 3 ∗ λ n = ∣ A ∣ \lambda_{1}*\lambda_{2}*\lambda_{3}*\lambda_{n}=|A| λ1∗λ2∗λ3∗λn=∣A∣

该证明用到高中时期的多项式的乘法规律。更关键的是明白 λ \lambda λ是 ∣ λ ∗ E − A ∣ = 0 |\lambda*E-A|=0 ∣λ∗E−A∣=0的根
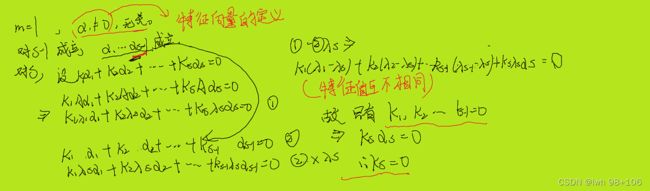
设A为n阶方阵, λ 1 \lambda_{1} λ1, λ 2 \lambda_{2} λ2, λ 3 \lambda_{3} λ3,…, λ m \lambda_{m} λm为A的m个不同特征值, a 1 , a 2 , a 3 . . . a m a_{1},a_{2},a_{3}...a_{m} a1,a2,a3...am分别为A的对应于 λ 1 \lambda_{1} λ1, λ 2 \lambda_{2} λ2, λ 3 \lambda_{3} λ3,…, λ m \lambda_{m} λm的特征向量,则 a 1 , a 2 , a 3 . . . a m a_{1},a_{2},a_{3}...a_{m} a1,a2,a3...am线性无关。
该证明采用数学归纳法
证明如下:
 设n阶方阵A的相异特征值为 λ 1 , λ 2 , . . . . λ n \lambda_{1},\lambda_{2},....\lambda_{n} λ1,λ2,....λn,对应于 λ i \lambda_{i} λi的线性无关的特征向量为 a i 1 , a i 2 , a i 3 . . . a i m a_{i1},a_{i2},a_{i3}...a_{im} ai1,ai2,ai3...aim,则向量组 a i 1 , a i 2 , a i 3 . . . a i m a_{i1},a_{i2},a_{i3}...a_{im} ai1,ai2,ai3...aim线性无关。
用一句话说就是,无关的无关还是无关。
其推导过程与上式类似。
K重特征根对应的线性无关的特征向量的个数小于等于K