线性代数笔记【二次型】
二次型
n元二次型:关于n个变量 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn的二次齐次函数
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ f(x_1,x_2,\cdo…
系数全为实数的二次型叫做实二次型,除此之外还有复二次型和复二次型矩阵,但在这里不讨论
标准二次型:只含平方项的二次型,形如 g ( y 1 , y 2 , ⋯ , y n ) = d 1 y 1 2 + d 2 y 2 2 + ⋯ + d n y n 2 g(y_1,y_2,\cdots,y_n)=d_1y_1^2+d_2y_2^2+\cdots+d_ny_n^2 g(y1,y2,⋯,yn)=d1y12+d2y22+⋯+dnyn2
规范二次型:形如 h ( z 1 , z 2 , ⋯ , z n ) = z 1 2 + z 2 2 + ⋯ + z p 2 − z p + 1 2 − ⋯ − z p + q 2 h(z_1,z_2,\cdots,z_n)=z_1^2+z_2^2+\cdots+z_p^2-z_{p+1}^2-\cdots-z_{p+q}^2 h(z1,z2,⋯,zn)=z12+z22+⋯+zp2−zp+12−⋯−zp+q2的二次型
规 范 二 次 型 ⊂ 标 准 二 次 型 ⊂ 二 次 型 规范二次型\subset 标准二次型 \subset 二次型 规范二次型⊂标准二次型⊂二次型
二次型矩阵
将二次型改写成矩阵形式:
$$
\left[
\begin{array}{cccc}
x_1,x_2,\cdots,x_n
\end{array}
\right]
\left[
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \
a_{21} & a_{22} & \cdots & a_{2n} \
\vdots & \vdots & & \vdots \
a_{n1} & a_{n2} & \cdots & a_{nn} \
\end{array}
\right]
\left[
\begin{array}{c}
x_1 \
x_2 \
\vdots \
x_n
\end{array}
\right]
$$
记 A = [ a i j ] n × n , x = [ x 1 , x 2 , ⋯ , x n ] T A=[a_{ij}]_{n \times n},x=[x_1,x_2,\cdots,x_n]^T A=[aij]n×n,x=[x1,x2,⋯,xn]T,则有 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx
其中A为对称矩阵,称为二次型f(x)的矩阵
因为二次型的表达方式不唯一,所以需要使用一个统一形式的矩阵来描述二次型,这就导致必须让二次型矩阵为对称矩阵
可以将A看成是系数矩阵,将x看成是变量矩阵,A的非对角元是 x m n x_{mn} xmn对应的系数,对角元则是平方项 x m n 2 x_{mn}^2 xmn2的系数,特别地,A的非对角元是 x i x j x_ix_j xixj系数的 1 2 \frac{1}{2} 21
二次型和对称矩阵之间一一对应,对称矩阵A的秩叫做二次型f(x)=xTAx的秩
线性变换
设A和x分别是m x n矩阵和n元列向量,把y=Ax叫做从n元向量x到m元向量y的线性变换
线性变换在转换的角度可以被看作是映射
当A为可逆矩阵时,y=Ax叫做可逆变换
当A为正交矩阵时,y=Ax叫做正交变换
正交变换是一种特殊的可逆变换,具有以下性质:
正交变换保持向量的内积、长度和夹角不变,在几何空间中能够保持几何图形不变
数学描述:设Q为n阶正交矩阵, x 1 ∈ R n , x 2 ∈ R n , y 1 = Q x 1 , y 2 = Q x 2 x_1 \in R^n,x_2 \in R^n,y_1=Qx_1,y_2=Qx_2 x1∈Rn,x2∈Rn,y1=Qx1,y2=Qx2, x 1 x_1 x1与 x 2 x_2 x2夹角为 θ \theta θ, y 1 y_1 y1与 y 2 y_2 y2夹角为 ϕ \phi ϕ,则 ( y 1 , y 2 ) = ( x 1 , x 2 ) , ∣ ∣ y 1 ∣ ∣ = ∣ ∣ x 1 ∣ ∣ , ϕ = θ (y_1,y_2)=(x_1,x_2),||y_1||=||x_1||,\phi=\theta (y1,y2)=(x1,x2),∣∣y1∣∣=∣∣x1∣∣,ϕ=θ
在二次型这一背景下,二次型矩阵A表征了二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx的形态,线性变换y=Px可以将某一二次型在参照系x中的“形态A”,变换成另一个参照系y下的“形态B”,由此引出了合同变换
合同变换
对于n阶方阵A和B,若存在可逆矩阵P,使 P T A P = B P^TAP=B PTAP=B,则称A与B合同(也称A与B相合)
变换 P T A P P^TAP PTAP叫做对A进行合同变换(也叫相合变换)
当A为对称矩阵时,可知B也是对称矩阵——合同变换不改变矩阵的对称性
二次型中两个合同矩阵就代表了同一个二次型在可逆线性变换下的两个不同状态的联系
合同具有三个基本性质:
- 反身性:矩阵A的一个合同矩阵是他本身
- 对称性:A与B合同,则B与A合同
- 传递性:A与B合同,B与C合同,则A与C合同
对二次型进行可逆变换的实质是对其矩阵进行合同变换
变换形式整理如下:
- 等价: P A Q = B PAQ=B PAQ=B,其中P、Q都是初等矩阵(单位矩阵经过一次初等变换得到的矩阵)
- 相似: P − 1 A P = B P^{-1}AP=B P−1AP=B
- 合同: P A P T = B PAP^T=B PAPT=B
有以下结论:
- 合同一定等价
- 相似一定等价
- 相似不一定合同,合同也不一定相似
- 若P为正交矩阵,则相似一定合同
用正交变换将二次型化为标准型
对于任给的n元二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx,总有正交变换 x = Q y x=Qy x=Qy能把f(x)化为标准型 g ( y ) = λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 g(y)=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2 g(y)=λ1y12+λ2y22+⋯+λnyn2,其中 λ 1 , λ 2 , ⋯ , λ n \lambda_1,\lambda_2,\cdots,\lambda_n λ1,λ2,⋯,λn是A的特征值,它们在标准型中的排列次序与它们对应的特征向量(Q的列向量)在正交矩阵Q中的排列次序一一对应
注意:正交变换只能化二次型为标准型,不能化为规范型(除非特征值是1、-1、0三者之一)
除了正交变换也能有其他变换将f(x)化为标准型,表达方式不唯一,系数可能会发生变化
用配方法把二次型化为标准型
配方法即拉格朗日配方法
如果二次型不含平方项,可先用一个可逆变换将其化为含有平方项的二次型,对于含有 x i 2 x_i^2 xi2的二次型,可先将含有 x i x_i xi的项集中起来进行配方,对于剩下的部分按照上述方法处理;如此迭代就可以得到标准型了
核心思想:先凑出平方项再进行配方
基本原则:若有平方项,要将平方项及与其相关的混合项一次配完成完全平方;如果没有平方项时,作可逆线性变换
{ x 1 = y 1 + y 2 x 2 = y 1 − y 2 x 3 = y 3 \left\{ \begin{aligned} x_1=y_1+y_2\\ x_2=y_1-y_2\\ x_3=y_3 \end{aligned} \right. ⎩⎪⎨⎪⎧x1=y1+y2x2=y1−y2x3=y3
使其出现平方项,再配完全平方
惯性定理
根据上面的两种变换方法,可以看出标准型不是唯一的,实际上标准型背后有一个“不变”的东西
用不同方法将二次型化成的标准型一般不同,但标准型所含的平方项的相输相同,其正、负平方项的项数对应相等,这个性质可以如下总结:
惯性定理:用任何可逆变换将n元二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx所化为的标准型的正负平方项的项数都对应相等
惯性定理反映了二次型在可逆变换下的一个不变的性质——正、负平方项的项数是唯一确定的,二次型的“不变量”就是正、负平方项的项数。将一个二次型的标准型的正、负平方项项数称为该二次型的正、负惯性指数
标准型的正负惯性指数与二次型矩阵的特征值相对应,有n个正特征值,二次型的正惯性指数就是n;有m个负特征值,二次型的负惯性指数就是m
若二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx的正、负惯性指数分别为p和q,则存在可逆变换 x = P y x=Py x=Py,将该二次型化为规范形 y 1 2 + y 2 2 + ⋯ + y p 2 − y p + 1 2 − ⋯ − y p + q 2 y_1^2+y_2^2+\cdots+y_p^2-y_{p+1}^2-\cdots-y_{p+q}^2 y12+y22+⋯+yp2−yp+12−⋯−yp+q2
与实对称矩阵A相合的对角矩阵的正、负对角元的个数叫做A的正、负惯性指数
都对应于实对称矩阵,也有惯性定理:用任何相合变换将实对称矩阵A所化为的对角矩阵的正、负对角元的个数都对应相等
二次型的本质属性可以通过对应矩阵的特征值来判别:
- 可以通过将二次型化为标准型来求其正、负惯性指数
- 可以通过求解其对应实对称矩阵的特征值来求其正、负惯性指数
若实对称矩阵A的正、负惯性指数分别为p和q,则A相合于对角矩阵 d i a g ( E p , − E q , O ) diag(E_p,-E_q,O) diag(Ep,−Eq,O),存在可逆矩阵P,使得 P T A P = d i a g ( E p , − E q , O ) P^TAP=diag(E_p,-E_q,O) PTAP=diag(Ep,−Eq,O),称 d i a g ( E p , − E q , O ) diag(E_p,-E_q,O) diag(Ep,−Eq,O)为实对称矩阵A的相合标准型
两个合同的实对称矩阵的正、负惯性指数不一定对应相等——如果两个合同的实对称矩阵同阶,则它们的正、负惯性指数相等
正定二次型与负定二次型
对于n元二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx,若对任意n元非零实向量x都有 f ( x ) > 0 f(x)>0 f(x)>0,则称该二次型为正定二次型,称A为正定矩阵。若对任意n元非零实向量x都有 f ( x ) < 0 f(x)<0 f(x)<0,则称该二次型为负定二次型,称A为负定矩阵
注意:在判断一个矩阵是否为正定、负定矩阵前首先要判断它是否是实对称矩阵
正定矩阵的基本性质
f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx为n元二次型,则下列命题互为充要条件:
- f(x)为正定二次型
- A为正定矩阵
- 对于任意 x ≠ 0 x\neq0 x=0,都有 x T A x > 0 x^TAx>0 xTAx>0
- A的顺序主子式均大于0
- A的特征值都为正数
- A的正惯性指数为n
- A相合于单位矩阵E
- 存在可逆矩阵P,使 P T A P = E P^TAP=E PTAP=E
- 存在n阶可逆矩阵B,使 A = B T B A=B^TB A=BTB
若n阶对称矩阵A是正定矩阵,则A的对角元 a i i > 0 ( i = 1 , 2 , ⋯ , n ) a_{ii}>0(i=1,2,\cdots,n) aii>0(i=1,2,⋯,n)且 ∣ A ∣ > 0 , t r ( A ) > 0 |A|>0,tr(A)>0 ∣A∣>0,tr(A)>0
如果A的对角元不全为正数,A一定不是正定矩阵;但当A的对角元全为正数,不能肯定A为正定矩阵
正定矩阵判别法
顺序主子阵:矩阵 A = [ a i j ] n × n A=[a_{ij}]_{n\times n} A=[aij]n×n的左上角k阶子阵称为A的k阶顺序主子阵,记作 A k A_k Ak
顺序主子式: A k A_k Ak的行列式,记作 ∣ A k ∣ |A_k| ∣Ak∣
实对称矩阵 A = [ a i j ] n × n A=[a_{ij}]_{n\times n} A=[aij]n×n为正定矩阵的充要条件是A的各阶顺序主子式都大于0
正定矩阵和正数的类似特性
合同变换不改变实对称矩阵的正定性
A为n阶实对称矩阵,则A为正定矩阵 <=> 存在正定矩阵B,使得 A = B 2 A=B^2 A=B2;同理,A为正定矩阵 <=> 存在负定矩阵C,使得 A = C 2 A=C^2 A=C2
A为负定矩阵 <=> -A为正定矩阵
设A和B是同阶正定矩阵,数c>0,k为正整数,则 A + B , c A , A k , A − 1 , A ∗ A+B,cA,A^k,A^{-1},A^* A+B,cA,Ak,A−1,A∗均为正定矩阵
通过这些性质,可以推导出负定矩阵和负数类似,具有下面的性质
负定矩阵的性质
设 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx为n元二次型,下列命题互为充要条件:
- f(x)为负定二次型
- A为负定矩阵
- A的特征值都为负数
- A的负惯性指数为n
- A合同于-E,E为单位矩阵
- 存在n阶可逆矩阵B,使 A = − B T B A=-B^TB A=−BTB
- A的奇数阶顺序主子式都小于0,偶数阶顺序主子式都大于0
负定矩阵可以通过加负号的方式转化为正定矩阵
半定矩阵和不定矩阵
半正定二次型和半正定矩阵:对于n元二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx,若对任意n元实向量x都有 f ( x ) ≥ 0 f(x)\ge0 f(x)≥0,且存在 x 0 ≠ 0 x_0\neq0 x0=0使 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0,则称该二次型为半正定二次型,并称A为半正定矩阵;若对任意n元实向量x都有 f ( x ) < 0 f(x)<0 f(x)<0,则存在 x 0 ≠ 0 x_0\neq0 x0=0使 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0,则称该二次型为半负定二次型,称A为半负定矩阵
若既存在 y ≠ 0 y\neq0 y=0使 f ( y ) > 0 f(y)>0 f(y)>0,又存在 z ≠ 0 z\neq0 z=0使 f ( z ) < 0 f(z)<0 f(z)<0,则称f(x)为不定二次型,称A为不定矩阵
对二次型问题的深入理解
二次型、矩阵之间的关系实质上是相互表征的关系
通过二次型可以反映矩阵的 A = x T A x A=x^TAx A=xTAx“形态”
二次型和矩阵的变换
二次型和矩阵变换的变换关系如下所示:
-
线性变换
通过一个线性变换系数矩阵将一个二次型变换为另一个二次型
x = C y x=Cy x=Cy
如果线性变换的系数矩阵C可逆,即 ∣ C ∣ ≠ 0 |C|\neq 0 ∣C∣=0,则这个变换称为可逆线性变换,简称可逆变换
如果线性变换的系数矩阵C为正交矩阵,即 C T C = E C^TC=E CTC=E,则这个变换称为正交线性变换,简称正交变换
线性变换是对矩阵线性性质的运用
-
合同变换
通过两个可逆矩阵使一个矩阵变换为另一个矩阵
对于n阶方阵A和B,若存在可逆矩阵C,使 C T A C = B C^TAC=B CTAC=B,则称A与B合同,变换 C T A C C^TAC CTAC叫做对A进行合同变换
对二次型/矩阵进行可逆变换的实质是对其矩阵进行合同变换,如下所示:
- 等价: P A Q = B PAQ=B PAQ=B,其中P、Q都是初等矩阵(单位矩阵经过一次初等变换得到的矩阵)
- 相似: P − 1 A P = B P^{-1}AP=B P−1AP=B,其中P是可逆矩阵
- 合同: P A P T = B PAP^T=B PAPT=B,或表示为 P T A P = B P^TAP=B PTAP=B,其中P是可逆矩阵
可以理解矩阵的可逆变换间具有以下性质:
- 合同一定等价
- 相似一定等价
- 相似不一定合同,合同也不一定相似
- 若P为正交矩阵,则相似一定合同
通过二次型之间的变换关系可以推导出以下结论:
- 可逆线性变换不改变矩阵/二次型的秩
- 和对称矩阵合同的矩阵必定是对称矩阵
二次型的标准型
只含有平方项、没有交叉项的二次型称为标准型
系数仅为1、0、-1的标准型称为规范形
若一个二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx合同于 d 1 x 1 2 + d 2 x 2 2 + ⋯ + d n x n 2 d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2 d1x12+d2x22+⋯+dnxn2标准形,则称 d 1 x 1 2 + d 2 x 2 2 + ⋯ + d n x n 2 d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2 d1x12+d2x22+⋯+dnxn2为二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx的合同标准形
若一个二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx合同于 x 1 2 + x 2 2 + ⋯ + x p 2 − x p + 1 2 − x p + 2 2 − ⋯ − x p + q 2 x_1^2+x_2^2+\cdots+x_p^2-x_{p+1}^2-x_{p+2}^2-\cdots-x_{p+q}^2 x12+x22+⋯+xp2−xp+12−xp+22−⋯−xp+q2标准形,则称 x 1 2 + x 2 2 + ⋯ + x p 2 − x p + 1 2 − x p + 2 2 − ⋯ − x p + q 2 x_1^2+x_2^2+\cdots+x_p^2-x_{p+1}^2-x_{p+2}^2-\cdots-x_{p+q}^2 x12+x22+⋯+xp2−xp+12−xp+22−⋯−xp+q2为二次型 f ( x ) = x T A x f(x)=x^TAx f(x)=xTAx的合同标准形
任何二次型都可以通过配方法(作可逆线性变换)化为标准型或规范形,也可以通过正交变换化成标准形
惯性定理
惯性定理:无论选取什么样的可逆线性变换,将二次型化成标准形或规范形,其正项的总数p和负项的总数q都不变,p称为正惯性指数,q称为负惯性指数
若二次型的秩为r,则r=p+q
合同变换不改变正负惯性指数
两个二次型或实对称矩阵合同的充要条件:有相同的正负惯性指数,或有相同的秩及正/负惯性指数
二次型正定的充要条件
以下命题互为充要条件:
- n元二次型 f = x T A x f=x^TAx f=xTAx正定
- 对任意 x ≠ 0 x\neq 0 x=0,有 x T A x > 0 x^TAx>0 xTAx>0
- f的正惯性指数p=n
- 存在可逆矩阵C,使 A = D T D A=D^TD A=DTD
- A和E合同
- A的特征值 λ i > 0 ( i = 1 , 2 , ⋯ , n ) \lambda_i>0(i=1,2,\cdots,n) λi>0(i=1,2,⋯,n)
- A的全部顺序主子式(从A的左上角开始沿主对角线依次取1、2、…、n阶行列式)均大于0
二次型正定的必要条件
二次型正定,可推出以下结论:
- a i i > 0 ( i = 1 , 2 , ⋯ , n ) a_{ii}>0(i=1,2,\cdots,n) aii>0(i=1,2,⋯,n)
- ∣ A ∣ > 0 |A|>0 ∣A∣>0
配方法化二次型为标准形
直接配方即可
正交变换化二次型为标准形
注意:正交变换只能化二次型为标准形,不能化为规范性(除非特征值都是0、1、-1之中的数)
正交变换将二次型化成的标准形唯一,形式为 λ 1 y 1 2 + λ 2 y 2 2 + ⋯ + λ n y n 2 \lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2 λ1y12+λ2y22+⋯+λnyn2
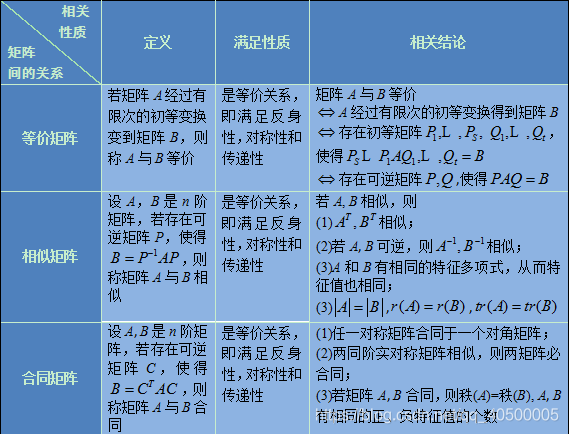
区分等价、相似、合同矩阵
- A、B是同型矩阵,则下列命题等价:
- A,B等价
- A能经过有限次初等变换得到B
- 有可逆矩阵P、Q,能使 P A Q = B PAQ=B PAQ=B
- r ( A ) = r ( B ) r(A)=r(B) r(A)=r(B)
- A、B是同阶方阵,下列命题等价:
- A,B相似
- 有可逆矩阵P,能使 P − 1 A P = B P^{-1}AP=B P−1AP=B
- A、B是同阶方阵,下列命题等价:
- A,B合同
- 有可逆矩阵P,能使 P T A P = B P^TAP=B PTAP=B
- x T A x , x T B x x^TAx,x^TBx xTAx,xTBx有相同的正负惯性指数,或有相同的秩序及正/负惯性指数