扫雷(蓝桥杯)
题目描述
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下, 在一个二维平面上放置着 n 个炸雷,第 i 个炸雷 (xi , yi ,ri) 表示在坐标 (xi , yi) 处存在一个炸雷,它的爆炸范围是以半径为 ri 的一个圆。
为了顺利通过这片土地,需要玩家进行排雷。玩家可以发射 m 个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第 j 个排雷火箭 (xj , yj ,rj) 表示这个排雷火箭将会在 (xj , yj) 处爆炸,它的爆炸范围是以半径为 rj 的一个圆,在其爆炸范围内的炸雷会被引爆。同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式
输入的第一行包含两个整数 n、m.
接下来的 n 行,每行三个整数 xi , yi ,ri,表示一个炸雷的信息。
再接下来的 m 行,每行三个整数 xj , yj ,rj,表示一个排雷火箭的信息。
输出一个整数表示答案。
样例输入
2 1
2 2 4
4 4 2
0 0 5
样例输出
2
提示
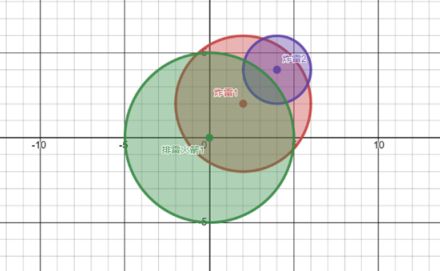
示例图如下,排雷火箭 1 覆盖了炸雷 1,所以炸雷 1 被排除;炸雷 1 又覆盖了炸雷 2,所以炸雷 2 也被排除。
对于 40% 的评测用例:0 ≤ x, y ≤ 109 , 0 ≤ n, m ≤ 103 , 1 ≤ r ≤ 10.
对于 100% 的评测用例:0 ≤ x, y ≤ 109 , 0 ≤ n, m ≤ 5 × 104 , 1 ≤ r ≤ 10.
第一种
图的深度优先遍历,邻接表实现, 由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9, 明显会超时。(WA)
#include
#include
#include
#include
#include
#define int long long
using namespace std;
const int N=5e3+10;
bool st[N];
int n,m;
//存炸弹
struct node
{
int x,y,r;
}stu[N];
vectorv[N];
//判断是否在这颗雷是否在这个圆
bool sqr(int x,int y,int xx,int yy,int r)
{
if((xx-x)*(xx-x)+(yy-y)*(yy-y)<=r*r) return true;
return false;
}
//连成一个连通图 雷在这个雷的范围内的就扩展
void add(int idx)
{
int x=stu[idx].x,y=stu[idx].y,r=stu[idx].r;
for(int i=1;i<=n;i++)
{
if(i!=idx)
{
if(sqr(x,y,stu[i].x,stu[i].y,r)) v[idx].push_back(i);
}
}
}
//看有多少颗符合要求的炸弹
int dfs(int idx)
{
int sum=1;
st[idx]=1;
for(int i=0;i>n>>m;
for(int i=1;i<=n;i++)
{
int x,y,r;cin>>x>>y>>r;
stu[i]={x,y,r};
}
for(int i=1;i<=n;i++)
{
add(i);
}
int sum=0;
for(int i=1;i<=m;i++)
{
int x,y,r;cin>>x>>y>>r;
sum+=dfs_Trave(x,y,r);
}
cout< 图的深度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
AC版
#include
#include
#include
#include
#include
#include 第二种
图的广度优先遍历,邻接表实现
由于点数有1e5,那么遍历所有图上的点是否联通,需要O(n^2)也就是需要2.5e9,
先把坐标按x轴从小到大排序,再按y轴从小到大排序
当许多坐标扎堆在同一点的时候,应当去掉重复的点,只留下半径最大的点。
不然建图的时候有O(n^2)的时间复杂度。
AC版
#include
#include
#include
#include
#include