代码随想录训练营 Day58打卡 图论part08 拓扑排序 dijkstra(朴素版)
代码随想录训练营 Day58打卡 图论part08
一、拓扑排序
例题:卡码117. 软件构建
题目描述
某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
输入描述
第一行输入两个正整数 N, M。表示 N 个文件之间拥有 M 条依赖关系。
后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
输出描述
输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
如果不能成功处理(相互依赖),则输出 -1。
输入示例
5 4
0 1
0 2
1 3
2 4
输出示例
0 1 2 3 4
提示信息
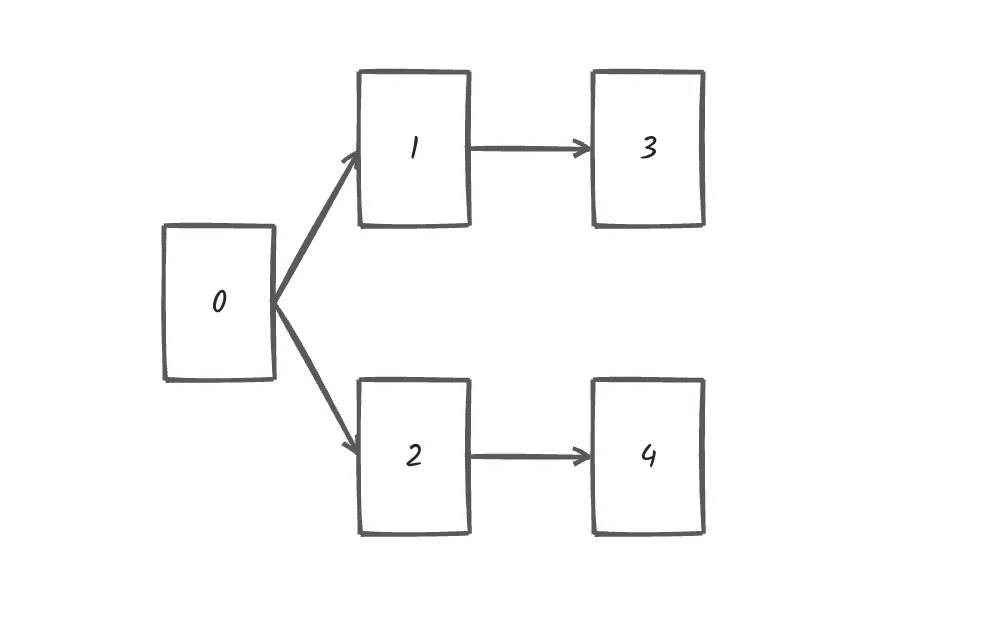
文件依赖关系如下:
所以,文件处理的顺序除了示例中的顺序,还存在
0 2 4 1 3
0 2 1 3 4
等等合法的顺序。
该代码的目标是通过拓扑排序来解决有向图中的依赖关系问题。具体来说,给定 n 个文件以及它们的依赖关系(即 m 条边),要求我们找出一种拓扑顺序,使得每个文件都能在它所依赖的文件之后被执行。如果无法找到合法的拓扑排序(即存在环),则输出 -1。
拓扑排序的定义:
拓扑排序是指对一个有向无环图(DAG)中的节点进行排序,使得对于每一条有向边 (u, v),节点 u 出现在节点 v 之前。换句话说,拓扑排序可以用于确定某些任务之间的依赖顺序。
算法思路
-
入度表:首先,为每个节点(文件)构建一个入度表,表示每个节点有多少条边指向它。即,如果一个文件有 k 个依赖的文件,那么它的入度为 k。
-
依赖关系图:使用邻接表(umap)来记录每个文件所依赖的其他文件。每个节点 s 指向其依赖的文件 t。
-
初始化队列:将所有入度为 0 的节点(即没有依赖的文件)加入队列中,这些节点可以作为排序的起始点。
-
BFS 过程:
(1)从队列中逐一取出节点,将其加入结果列表。
(2)对每个节点 cur 的依赖节点(指向的文件)进行处理,更新它们的入度表(减少它们的入度)。
(3)如果某个节点的入度变为 0,表示它的所有依赖文件已经处理完毕,可以加入队列进行处理。 -
检测环路:如果拓扑排序完成后,结果中包含的节点数不等于总节点数,说明存在环路,无法完成排序,此时返回 -1。
代码实现
from collections import deque, defaultdict
def topological_sort(n, edges):
inDegree = [0] * n # inDegree 数组记录每个节点的入度,初始为0
umap = defaultdict(list) # 邻接表,记录节点之间的依赖关系,默认为空列表
# 构建图和入度表
for s, t in edges:
inDegree[t] += 1 # 每当一个节点被指向,其入度增加
umap[s].append(t) # s 指向 t,添加到邻接表中
# 初始化队列,将所有入度为0的节点加入队列
queue = deque([i for i in range(n) if inDegree[i] == 0])
result = [] # 结果数组,用于存储拓扑排序的结果
# 开始广度优先搜索(BFS)
while queue:
cur = queue.popleft() # 当前队列中的节点,已无任何依赖
result.append(cur) # 将其加入结果列表中
for file in umap[cur]: # 遍历该节点指向的所有节点
inDegree[file] -= 1 # 当前节点的出度边被移除,其指向节点的入度减1
if inDegree[file] == 0: # 如果入度变为0,说明该节点可以被处理
queue.append(file) # 将其加入队列
# 如果拓扑排序中包含所有节点,说明排序成功;否则,说明有环
if len(result) == n:
print(" ".join(map(str, result))) # 打印排序结果
else:
print(-1) # 如果结果不包含所有节点,输出-1,表示图中有环
# 主程序,读取输入
if __name__ == "__main__":
# 读取节点数量 n 和边的数量 m
n, m = map(int, input().split())
# 读取 m 条边,每条边由两个整数 s 和 t 表示
edges = [tuple(map(int, input().split())) for _ in range(m)]
# 调用拓扑排序函数
topological_sort(n, edges)
卡码题目链接
题目文章讲解
二、dijkstra(朴素版)
例题:卡码47. 参加科学大会
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。
小明的起点是第一个车站,终点是最后一个车站。然而,途中的各个车站之间的道路状况、交通拥堵程度以及可能的自然因素(如天气变化)等不同,这些因素都会影响每条路径的通行时间。
小明希望能选择一条花费时间最少的路线,以确保他能够尽快到达目的地。
输入描述
第一行包含两个正整数,第一个正整数 N 表示一共有 N 个公共汽车站,第二个正整数 M 表示有 M 条公路。
接下来为 M 行,每行包括三个整数,S、E 和 V,代表了从 S 车站可以单向直达 E 车站,并且需要花费 V 单位的时间。
输出描述
输出一个整数,代表小明从起点到终点所花费的最小时间。
输入示例
7 9
1 2 1
1 3 4
2 3 2
2 4 5
3 4 2
4 5 3
2 6 4
5 7 4
6 7 9
输出示例
12
提示信息
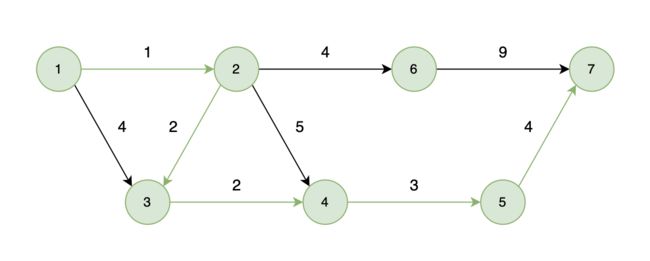
能够到达的情况:
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
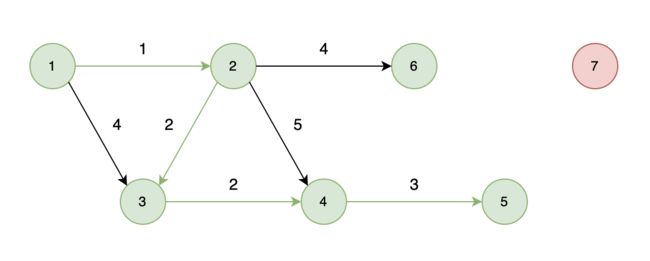
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
Dijkstra算法的基本步骤:
-
初始化:
设定源点到自己的距离为0,其他节点的距离为无穷大。
使用一个布尔数组 visited 来记录哪些节点已经被处理过,防止重复处理。 -
选择未访问的节点中距离源点最近的节点:
遍历所有未访问的节点,选择距离源点最近的节点 cur。 -
更新与该节点相连的未访问节点的最短距离:
对于当前节点 cur,检查与其相连的所有节点,更新它们到源点的距离。如果通过 cur 到达某个未访问节点的距离小于已知最短距离,则更新该节点的最短距离。 -
重复选择节点,直到所有节点都被访问过,或者没有可到达的未访问节点。
实现细节:
- 邻接矩阵:我们使用一个 grid 矩阵来表示图,grid[i][j] 表示从节点 i 到节点 j 的边权重。初始化时,所有边的权重为无穷大float(‘inf’),表示没有连接。
- 距离数组:minDist 用于记录源点到每个节点的最短距离。
- 访问标记数组:visited 用于记录哪些节点已经处理完毕。
版本一 dijkstra(朴素版)
import sys
def dijkstra(n, m, edges, start, end):
# 初始化邻接矩阵 grid,大小为 (n+1) x (n+1),初始值为无穷大,表示没有连接的边
grid = [[float('inf')] * (n + 1) for _ in range(n + 1)]
# 填充邻接矩阵,将每条边的权重记录到矩阵中
for p1, p2, val in edges:
grid[p1][p2] = val # 从节点 p1 到节点 p2 的边权重为 val
# 初始化最短距离数组 minDist,所有节点的最短距离初始为无穷大
minDist = [float('inf')] * (n + 1)
# 初始化访问数组 visited,记录每个节点是否已经被访问
visited = [False] * (n + 1)
# 起点的最短距离为0(起点到起点的距离为0)
minDist[start] = 0
# 进行 n 次遍历,每次选择一个节点加入到已处理的集合中
for _ in range(1, n + 1): # 遍历所有节点
minVal = float('inf') # 当前最小的距离
cur = -1 # 当前选择的节点
# 遍历所有节点,选择未访问过的且距离源点最近的节点
for v in range(1, n + 1):
if not visited[v] and minDist[v] < minVal:
minVal = minDist[v]
cur = v
if cur == -1: # 如果没有找到未访问的节点,提前结束
break
# 将当前选中的节点标记为已访问
visited[cur] = True
# 更新与当前节点相邻的未访问节点的距离
for v in range(1, n + 1):
# 如果 v 未访问且有从 cur 到 v 的边,并且通过 cur 到 v 的距离比现有的距离更短
if not visited[v] and grid[cur][v] != float('inf') and minDist[cur] + grid[cur][v] < minDist[v]:
# 更新节点 v 的最短距离
minDist[v] = minDist[cur] + grid[cur][v]
# 返回从起点 start 到终点 end 的最短距离
# 如果终点的距离仍为无穷大,表示不可达,返回 -1
return -1 if minDist[end] == float('inf') else minDist[end]
# 主程序,处理输入并调用 Dijkstra 算法
if __name__ == "__main__":
input = sys.stdin.read # 读取输入
data = input().split() # 按空格分割输入数据
n, m = int(data[0]), int(data[1]) # n 表示节点数,m 表示边数
# 读取 m 条边,每条边由起点 p1、终点 p2 和边权重 val 组成
edges = []
index = 2
for _ in range(m):
p1 = int(data[index])
p2 = int(data[index + 1])
val = int(data[index + 2])
edges.append((p1, p2, val)) # 将边加入到 edges 列表中
index += 3
# 起点为 1,终点为 n
start = 1 # 设置起点
end = n # 设置终点
# 调用 Dijkstra 算法计算从起点到终点的最短路径
result = dijkstra(n, m, edges, start, end)
# 输出最短路径的距离
print(result)
版本一 dijkstra(堆优化版)
堆优化的 Dijkstra 算法 相对于传统的 Dijkstra 算法,是通过使用 小顶堆 来加速寻找最短路径的节点。我们不再通过遍历所有节点来选择未访问且最近的节点,而是通过小顶堆高效地获取当前最小的路径节点。这种优化能显著减少计算量,尤其是在边稀疏的图中。
三部曲的改进:
- 选取最近的节点:我们通过一个小顶堆来存储每个节点到源点的最短路径,并每次从堆顶取出路径最短的节点进行处理。
- 标记为已访问:从堆中取出的节点为当前未访问的节点中距离最小的,标记该节点为已访问。
- 更新其他节点的最短距离:遍历该节点的所有相邻节点,更新它们到源点的最短距离,并将更新后的距离加入堆中。
import heapq # 导入heapq库,用于实现小顶堆
# 定义 Edge 类,表示一条边,包含目标节点和边的权值
class Edge:
def __init__(self, to, val):
self.to = to # 边的目标节点
self.val = val # 边的权值
# 堆优化的 Dijkstra 算法实现
def dijkstra(n, m, edges, start, end):
# 初始化邻接表,使用列表存储与每个节点相连的边
grid = [[] for _ in range(n + 1)] # n + 1,因为节点编号从 1 开始
# 构建邻接表,将每条边添加到对应的节点列表中
for p1, p2, val in edges:
grid[p1].append(Edge(p2, val)) # 记录 p1 到 p2 的边,权值为 val
# 初始化最短距离数组,所有节点的初始最短距离为无穷大
minDist = [float('inf')] * (n + 1)
# 初始化访问数组,记录节点是否已被访问
visited = [False] * (n + 1)
# 小顶堆,堆中存储 (距离, 节点) 元组
pq = []
# 将起点加入堆中,起点到自身的距离为 0
heapq.heappush(pq, (0, start))
minDist[start] = 0 # 起点到自身的距离为 0
# 处理堆中的节点
while pq:
cur_dist, cur_node = heapq.heappop(pq) # 从堆中取出距离最近的节点
if visited[cur_node]: # 如果该节点已经访问过,跳过
continue
visited[cur_node] = True # 标记该节点为已访问
# 遍历当前节点的所有邻接边
for edge in grid[cur_node]:
# 如果目标节点未访问过,且通过当前节点的路径更短,则更新该路径
if not visited[edge.to] and cur_dist + edge.val < minDist[edge.to]:
# 更新目标节点的最短距离
minDist[edge.to] = cur_dist + edge.val
# 将更新后的 (最短距离, 目标节点) 加入堆中
heapq.heappush(pq, (minDist[edge.to], edge.to))
# 如果终点的最短距离仍为无穷大,说明不可达,返回 -1;否则返回最短距离
return -1 if minDist[end] == float('inf') else minDist[end]
# 读取输入数据并调用 Dijkstra 算法
if __name__ == "__main__":
# 输入节点数 n,边数 m
n, m = map(int, input().split())
# 输入每条边的信息,边的格式为 (起点, 终点, 权值)
edges = [tuple(map(int, input().split())) for _ in range(m)]
# 设置起点和终点
start = 1 # 默认起点为 1
end = n # 默认终点为 n
# 调用 Dijkstra 算法计算从起点到终点的最短路径
result = dijkstra(n, m, edges, start, end)
# 输出最短路径结果
print(result)
详细说明:
-
邻接表的构建:
grid = [[] for _ in range(n + 1)]:初始化一个邻接表,grid[i] 表示节点 i 的所有相邻节点及其边的权重。
遍历输入的边,构建邻接表,将每条边加入到对应的起点节点的列表中。 -
小顶堆的使用:
使用 Python 的 heapq 模块实现小顶堆。堆中存储 (距离, 节点) 元组,每次取出距离最小的节点。
heapq.heappush(pq, (0, start)):将起点的距离(0)和起点节点加入堆中。
heapq.heappop(pq):从堆中取出距离最小的节点,并对其进行处理。 -
更新最短路径:
对于当前取出的节点 cur_node,遍历它所有的邻接节点,计算通过 cur_node 到达邻接节点的距离是否更短。如果更短则更新最短距离,并将其加入堆中。 -
提前退出:
如果当前从堆中取出的节点已经访问过,直接跳过,这样可以避免重复处理。 -
返回结果:
如果终点节点 end 的最短距离为无穷大,说明不可达,返回 -1;否则返回从起点到终点的最短距离。
堆优化的思路:
- 使用小顶堆时,所有边的处理顺序已经由堆的结构自动排序成了从最短到最长的顺序。因此不需要每次遍历所有未访问节点来查找最短路径,这样可以显著提高算法效率。
- 通过小顶堆优化后,Dijkstra 算法的时间复杂度从 O(n^2) 降低到 O(E log V),其中 E 是边的数量,V是节点的数量。这在处理稀疏图时效率非常高。
卡码题目链接
题目文章讲解