AI基础 L13 Constraint Satisfaction Problems I约束满足问题

Defining Constraint Satisfaction Problems

A constraint satisfaction problem (CSP) consists of three components, X, D, and C:
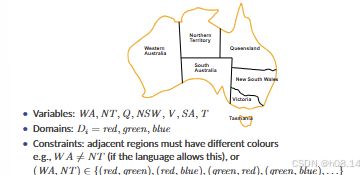
• X is a set of variables, {X1, . . . , Xn}.
• D is a set of domains, {D1, . . . , Dn}, one for each variable
• C is a set of constraints that specify allowable combination of values CSPs deal with assignments of values to variables.
• A complete assignment is one in which every variable is assigned a value
— A solution to a CSP is a consistent, complete assignment.
• A partial assignment is one that leaves some variables unassigned.
• Partial solution is a partial assignment that is consistent

约束满足问题（CSP）

约束满足问题是一个由三个主要组成部分组成的问题类型：

1. 变量集（X）：

   • 变量集 X 包含一组变量，通常表示为 {X1, . . . , Xn}。每个变量代表问题中的一个决策点或决策元素。

2. 域集（D）：

   • 域集 D 包含一组域，每个域对应一个变量，表示为 {D1, . . . , Dn}。域 Di 包含所有可能的值，每个值可以被分配给变量 Xi。

3. 约束集（C）：

   • 约束集 C 包含一组约束，这些约束定义了变量值之间的允许组合。这些约束限制了变量可以取的值，以保证问题的解是有效的。

CSPs 涉及的任务

CSPs 涉及的任务是分配值给变量，以满足所有约束。

解（Solution）

• 完整分配（Complete assignment）：

  • 完整分配是指每个变量都被分配了一个值。
  • 解决方案（Solution）：
    • CSPs 的解决方案是一个一致的、完整的分配，即满足所有约束的分配。

• 部分分配（Partial assignment）：

  • 部分分配是指一些变量没有分配值。
  • 部分解决方案（Partial solution）：
    • 部分解决方案是一个一致的、部分分配，即满足当前分配下所有约束的分配。

• Standard search problem:
— state is a “black box” — any old data structure that supports goal test, eval, successor
• CSP:
— state is defined by variables Xi with values from domain Di
— goal test is a set of constraints specifying allowable combinations of values for subsets of variables
• Simple example of a formal representation language
• Allows useful general-purpose algorithms with more power than standard search algorithms

• 状态（State）：

  • 状态可以是任何数据结构，只要它能够存储和更新问题状态的信息。

• 目标测试（Goal test）：

  • 目标测试是一个函数，用于判断当前状态是否达到了问题的目标状态。

• 评估（Evaluation）：

  • 评估函数用于评估当前状态的优劣，这通常用于启发式搜索算法中。

• 成功继任者（Successor）：

  • 成功继任者函数用于从当前状态生成新的状态，这些新状态是当前状态的合法继任者。

Map-Colouring

 

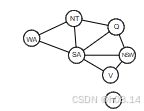
Constraint graph

• Binary CSP: each constraint relates at most two variables
• Constraint graph: nodes are variables, arcs show constraints

General-purpose CSP algorithms use the graph structure

Varieties of CSPs
• Discrete variables
— finite domains; size d ⇒ O(dn) complete assignments
e.g., Boolean CSPs, incl. Boolean satisfiability (NP-complete)
infinite domains (integers, strings, etc.)
e.g., job scheduling, variables are start/end days for each job
— need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3
— linear constraints solvable, nonlinear undecidable
• Continuous variables
e.g., start/end times for Hubble Telescope observations
— linear constraints solvable in poly time by LP methods
• Unary constraints involve a single variable,
e.g., S A̸ = green
• Binary constraints involve pairs of variables,
e.g., S A̸ = W A
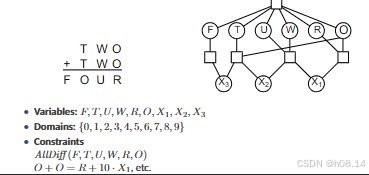
• Higher-order constraints involve 3 or more variables,
e.g., cryptarithmetic column constraints
• Preferences (soft constraints),
e.g., red is better than green
• often representable by a cost for each variable assignment
→ constrained optimization problems

离散变量的CSPs

离散变量的CSPs涉及具有有限域的变量，例如布尔变量、整数、字符串等。

• 特点：
  • 变量具有有限域，如布尔值、整数或字符串。
  • 解决方案的数量随着变量数量的增加而指数级增长。

无限域的CSPs

无限域的CSPs涉及具有无限域的变量，例如整数、字符串等。

• 特点：
  • 变量具有无限域，如整数或字符串。
  • 需要一种约束语言来表达变量之间的约束关系。
  • 线性约束是可解决的，但非线性约束是不可判定的。

连续变量的CSPs

连续变量的CSPs涉及具有连续域的变量，例如天文观测的开始和结束时间。

• 特点：
  • 变量具有连续域，如时间或空间。
  • 可以使用线性规划方法解决线性约束。
  • 非线性约束的解决可能需要更复杂的方法。

约束的类型

• 单变量约束（Unary constraints）：

  • 涉及单个变量，例如 S ≠ green。

• 二变量约束（Binary constraints）：

  • 涉及两个变量的关系，例如 S ≠ W。

• 高阶约束（Higher-order constraints）：

  • 涉及三个或更多变量的关系，例如密码算术列约束。

偏好约束（Preferences）

偏好约束是软约束，它们为每个变量分配了一个成本，表示对某个变量的偏好。

• 特点：
  • 偏好约束可以表示为对每个变量分配的成本。
  • 偏好约束通常用于约束优化问题。

eg  Cryptarithmetic