【编译原理】方舟编译技术课程 — 词法分析

打开目录阅读更佳
参考视频：方舟·编译技术入门与实战 以及 西交冯博琴老师的相关视频

编译的过程包括 词法分析（分析程序符号）、语法分析（分析语法单位）、中间代码生成、代码优化和目标代码生成。

一、编译过程各部分的任务

（1）词法分析：输入源程序，扫描分解源程序字符串，识别五类符号，包括定义符、标识符、运算符、界符和常数，转为单词符号。
（2）语法分析：在词法分析基础上，将单词符号转为语法单位（如短句、子句、句子、程序段、程序等），并确定整个输入串在语法上是否正确。语法分析主要做三件重要事情：一是程序入口在哪；二是中间怎么处理；三是得到的结果是什么。
（3）中间代码生成：有时也称之为语义分析，它对语法分析所识别出的各类语法单位，分析其含义，并进行初步翻译（即产生中间代码）。
（4）代码优化：主要针对中间代码进行加工变换，希望产生更高效，即节省空间和时间，的目标代码。
（5）目标代码生成：将中间代码转换为特定机器上的目标代码。

学习的方法：建立知识地图 ️
对一个新领域的探索，需要快速建立知识地图。
有限的时间，有限的注意力和有限的体力，要求我们在尽可能短的时间内高质量获取知识。

1.1 编译器整体架构和前端设计

来自 Rice University 的 Cooper 教授 COMP 412 课程的课件。

编译器的前端部分包括词法分析器、解释器和语义阐述器（非必需？），前端输出为中间代码或中间表示 Intermediate Representation (IR)，传给优化器，优化后的 IR 再传给后端，得到目标代码。

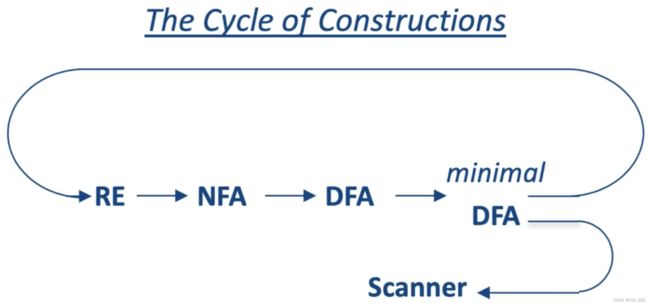
二、词法分析知识地图

来自 Rice University 的 Cooper 教授 COMP 412 课程的课件，如何构造出一个 Scanner。

术语解释：（有 minimal NFA 么？）

1. RE - 正则表达式（通常缩写为 regex ）
2. NFA - 非确定性有限自动机
3. DFA - 确定性有限自动机
4. minimal DFA - 最小DFA
5. Scanner - 词法分析器

各形式间相互转换采用的技术

词法分析几个算法的掌握程度：（1）掌握正则表达式的概念和写法，需要注意细节；（2）能够手工构造 RE -> NFA、NFA -> DFA；（3）理解 DFA -> minimal DFA 的算法思想；

2.1 正则表达式 Regular Expression

有一篇文章总结得蛮好：何为正则？ 涛叔正则表达式
大陆的翻译是“正则”，湾湾的翻译的“正规”，实际上就是一些约定俗成的规则，满足这些规则，视为表达式匹配成功。

首先从抽象的宏观层面理解 RE，分别是 交并补 的集合论观点。
（一）交集规则：若 A 和 B 是两个正则表达式，那么 AB 也是正则表达式，表示既匹配 A 也匹配 B。可以串联，如 ABCD。
（二）并集规则：若 A 和 B 是两个正则表达式，那么 A | B 表示满足匹配 A 或 B。多个并集时，可以表示为 A | B | C | D，也可以简记为 [ABCD]，两者表达的含义都是并集。
（三）补集规则：由 De Morgan’s Laws，取反后，逻辑或变为逻辑与，因此 [^AB] 是补集的写法，表示既不匹配 A 也不匹配 B。

然后从细致的微观层面了解具体的匹配规则。
（一）单字符匹配

字符	含义	连字符简化	转义符简化	取反及含义
a、b、c、1、2	单个字母或数字
[0123456789]	并集，所有可能的数字	[0-9]	\d	\D = [^0-9]，匹配所有非数字字符
[abcde…xyz]	并集，匹配所有小写字母	[a-z]
[ABCDE…XYZ]	并集，匹配所有大写字母	[A-Z]
[abc…xyzABC…XYZ]	并集，匹配所有字母，不区分大小写	[a-zA-Z]	\a	\A = [^a-zA-Z]，匹配所有非字母字符
	匹配所有大小写字母、数字和下划线	[a-zA-Z0-9_]	\w	\W = [^a-zA-Z0-9_]
空格	空格		\s	\S，匹配所有非空格字符
[^\n]	匹配除 \n 外的所有字符		.（句点）

（二）多字符匹配
大括号 {1, 3} 中数字的含义：第一个数字表示至少匹配的次数；第二个数字表示至多匹配的次数。

多字符	含义	大括号简化	进一步简化
\d\d	匹配两位数
\d | \d\d | \d\d\d	匹配一位数或两位数或三位数	\d{1, 3}
\d | \d\d | …	匹配任意（大于等于1）位数	\d{1,}	\d+
	匹配任意（大于等于0）位数	\d{0,}	\d*
a | ab	b 不出现或出现一次	ab{0, 1}	ab?

最后是 RE 的高级内容，包括贪心、引用和环视等，详情见链接文章。

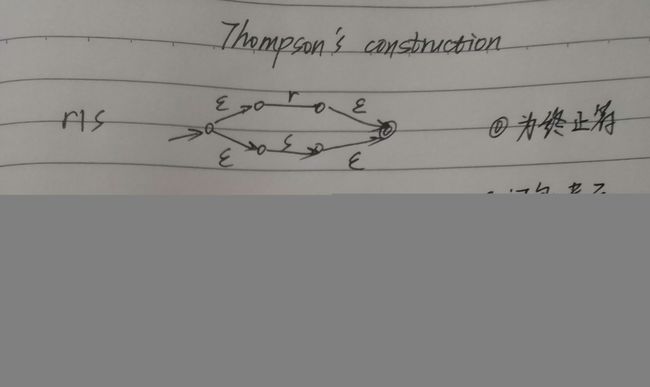
2.2 RE -> NFA 和 NFA -> DFA

RE 转 NFA 采用 Thompson’s construction，这是国外教材的普遍用法，但国内如哈工大在教学时，采用的方法更简洁但可能不够严谨（参考该博客的观点）。但对于理解概念，两者都没问题，下面以 Thompson’s construction 为参考。

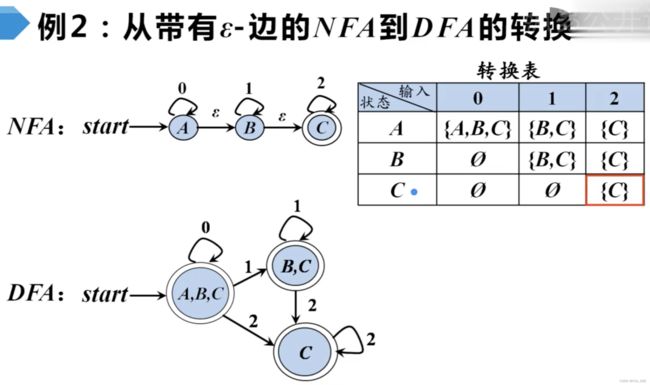
NFA 转 DFA采用 Subset construction （子集构造法），思路很简单，忘记如何构造时请参考哈工大陈鄞 (读作“银”) 教授的 mooc。

2.3 DFA 最小化思想

所谓 DFA 最小化就是优化 DFA 图，使其状态数最少。那么如何评估状态的数量呢？需要引入新的概念，可区分和不可区分。

通俗理解这个概念就是，（1）若状态集合，如 {A, B}，接受某个输入符号，转移发生歧义，得到不同的结果，则认为它们可区分，因为相同输入，输出不同。（2）若状态集合，如 {A,B,C} ，无论接受什么输入符号，都能转移到相同的结果，则认为它们不可区分，已经达到你中有我，我中有你的境界。

三、数学概念补充

记忆以下观点：

1. 编译器中大量算法处理的是离散空间的最优解问题。
2. 大量问题是 NP 问题，即没有多项式时间的解法。
3. 因此编译器中大量使用启发式（heuristic）算法寻找近似解，启发式 = 专家的猜测。