合并两个有序的子序，要求空间复杂度为O(1)

百度2012实习生校园招聘笔试题

数组al[0,mid-1]和al[mid,num-1]是各自有序的，对数组al[0,num-1]的两个子有序段进行merge，得到al[0,num-1]整体有序。要求空间复杂度为O(1)。注：al[i]元素是支持'<'运算符的。

先是琢磨良久，是否可能时间复杂度为O(n)，因为这让我想起了，左旋转数组的相关的算法。深陷下去后，突然什么光一闪。。。

果断放弃，使用最简单的算法，几分钟笔墨，错改调。（上次就是如此深陷泥潭而不可自拔）：

 1 void swap(int *a, int *b)

 2 {

 3     int tmp;

 4 

 5     tmp = *a;

 6     *a = *b;

 7     *b = tmp;

 8 }

 9 

10 void func(int a[], int n)

11 {

12     int i,j;

13 

14     if (n<=0)

15     {

16         return;

17     }

18     i = 0;

19     j = n/2;

20 

21     while(j<n && i<j)

22     {

23         if (a[i]<=a[j])

24         {

25             i++;

26         }

27         else

28         {

29             swap(a[i], a[j]);

30             for (int k=j-1;k>i; k--)

31             {

32                 swap(a[k], a[k+1]);

33             }

34             i++;

35             j++;

36         }

37     }

38 

39 }

算法简单，最坏的时间复杂度为O(n^2)。 

 

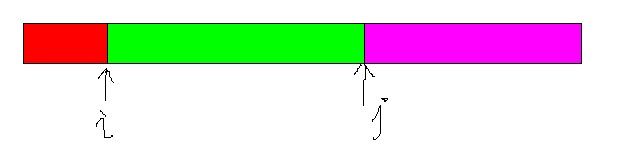
红色的区域是已排好的，绿色为前一子序，紫红为后子序；比较前后子序的最小元素，小的放入红色区域。

如果i的小，只需要往前一步；否则i与j的元素互换，各自向前一步；但此时导致前子序不再有序，通过调整恢复有序即可；

接着又网上搜索工作，找到一个block swapping。懒得看完，但却给了我提示，算法可以优化；

之前所说的调整恢复其实就是一个右移了一位，每当j中有元素较小时，就需要前移到红色区域中，这样导致了要移位；

试想j的后面有几个连续的元素都比i 小，这样每次就会导致j-i个移动元素；所以改动一下，没有每次都移动，等到j开始比i大的时候，

才开始移位，这时应用之前的“左移k的算法（貌似就是block swapping）”，其实时间复杂度为O(n)，所以当j连续比i小的数很多，效率就比较高了。

例如：1 6 9 12 2 3 4 15

1、i=0；j=4；a[i]<a[j] 所以i++

2、i=1; j=4; a[i]>a[j] 所以交换为 1 2 9 12 6 3 4 15; i++;j++

3、i=2; j=5; a[i]>a[j] 所以交换为 1 2 3 12 6 9 4 15; i++; j++

4、i=3; j=6; a[i]<a[j] 已经a[j]开始小了，1 2 3 12 6 9 4 15，所以这时蓝色部分就要一次右移两位（两个连续的小），移位后1 2 3 6 9 12 4 15

5、之后，沿袭刚才的思想，继续下去。。。

这样只是稍微的优化一下而已。又是一番折腾

 1 void reverse(int a[], int i, int j)

 2 {

 3 

 4     if (j-i<1)

 5     {

 6         return;

 7     }

 8     for (;i<j; i++,j--)

 9     {

10         swap(&a[i], &a[j]);

11     }

12 }

13 

14 void rightmove(int a[], int i, int j, int k)

15 {

16     if (j-i<1)

17     {

18         return;

19     }

20 

21     reverse(a, i, j-k);

22     reverse(a, j-k+1, j);

23     reverse(a, i, j);

24 }

25 

26 void func1(int a[], int n)

27 {

28     int i,j,tmp;

29     i=0;

30     j = n/2;

31     while(i<j&& j<n)

32     {

33         tmp = j;

34         while(i<j && a[i]<=a[j])

35         {

36             i++;

37         }

38         while(i<j && a[j]< a[i])

39         {            

40             swap(&a[i], &a[j]);

41             j++;

42         }

43 

44         rightmove(a, i+1, j-1, j-tmp);

45         i++;

46     }

47 }

结果看了看标准答案，华丽地把哥的秒了：

 1 /*

 2 数组a[begin, mid] 和 a[mid+1, end]是各自有序的，对两个子段进行Merge得到a[begin , end]的有序数组。 要求空间复杂度为O(1)

 3 方案：

 4 1、两个有序段位A和B，A在前，B紧接在A后面，找到A的第一个大于B[0]的数A[i]， A[0...i-1]相当于merge后的有效段，在B中找到第一个大于A[i]的数B[j]，

 5 对数组A[i...j-1]循环右移j-k位，使A[i...j-1]数组的前面部分有序

 6 2、如此循环merge

 7 3、循环右移通过先子段反转再整体反转的方式进行，复杂度是O(L), L是需要循环移动的子段的长度

 8 */

 9 #include<iostream>

10 using namespace std;

11 

12 void Reverse(int *a , int begin , int end )   //反转

13 {

14     for(; begin < end; begin++ , end--)

15         swap(a[begin] , a[end]);

16 }

17 void RotateRight(int *a , int begin , int end , int k)    //循环右移

18 {

19     int len = end - begin + 1;  //数组的长度

20     k %= len;

21     Reverse(a , begin , end - k);

22     Reverse(a , end - k + 1 , end);

23     Reverse(a , begin , end);

24 }

25 

26 // 将有序数组a[begin...mid] 和 a[mid+1...end] 进行归并排序

27 void Merge(int *a , int begin , int end )

28 {

29     int i , j , k;

30     i = begin;

31     j = 1 + ((begin + end)>>1);    //位运算的优先级比较低，外面需要加一个括号，刚开始忘记添加括号，导致错了很多次

32     while(i <= end && j <= end && i<j)

33     {

34         while(i <= end && a[i] < a[j])

35             i++;

36         k = j;   //暂时保存指针j的位置

37         while(j <= end && a[j] < a[i])

38             j++;

39         if(j > k)

40             RotateRight(a , i , j-1 , j-k);   //数组a[i...j-1]循环右移j-k次

41         i += (j-k+1);  //第一个指针往后移动，因为循环右移后，数组a[i....i+j-k]是有序的

42     }

43 }

44 

45 void MergeSort(int *a , int begin , int end )

46 {

47     if(begin == end)

48         return ;

49     int mid = (begin + end)>>1;

50     MergeSort(a , begin , mid);   //递归地将a[begin...mid] 归并为有序的数组

51     MergeSort(a , mid+1 , end);   //递归地将a[mid+1...end] 归并为有序的数组

52     Merge(a , begin , end);       //将有序数组a[begin...mid] 和 a[mid+1...end] 进行归并排序

53 }

54 

55 int main(void)

56 {

57     int n , i ;

58     //    int a[] = {1, 5,6,7,15,66, 2,3,4,8,33,35};

59     int a[] = {1 ,6 ,9 , 2 ,3,4 ,15};

60     

61     n = sizeof(a)/sizeof(int);

62     

63     MergeSort(a , 0 , n - 1);

64     

65     for(i = 0 ; i < n ; ++i)

66         cout<<a[i]<<" ";

67     

68     return 0;

69 }

咋一看，和哥的像，太像了；可是算法的思想的是两码事。（思考：1 3 5 7 2 4 6 8,我的算法则将要退化）

答案的思想高明要与结合了，归并（分治）的思想。继续考虑刚才的例子：

1 6 9 12 2 3 4 15

1、递归到底，将数组分每个元素为一个子序列，显然有序

2、退上一层，两个一组，1 6 | 9 12 | 2 3 | 4 15，依然有序

3、退上一层，四个一组，1 6 9 12 | 2 3 4 15

4、退上一层，8个一组，1 2 3 4 6 12 15

坑爹啊~这不是和哥的算法一样么。。。。其实是这样的当只有偶数个的时候，就退化为第二个算法了。

因为其每次的分组刚好是有序的，只有退回至最上层的时候，才需要真正移位。

再考虑 1 ,6 ,9 , 2 ,3,4 ,15

1、递归到底，将数组分每个元素为一个子序列，显然有序

2、退上一层，两个一组，1 6 | 9  2 | 3 4 | 15=>1 6 | 2 9 | 3 4 | 15

3、退上一层，四个一组，1 2 6 9 | 3 4 15

4、退上一层，7个一组，1 2 3 4 6 9 15

其实回想起来，没见得算法三很好，而且使用了两个递归。至于效率上，隐约感觉算法三稍比算法二的好；

毕