POJ 3352 Road Construction (边双连通分量)
题意 ：有一个景点要修路，但是有些景点只有一条路可达，若是修路的话则有些景点就到不了，所以要临时搭一些路，以保证无论哪条路在修都能让游客到达任何一个景点
思路 ：把景点看成点，路看成边，看要加几条边使这个图变成双连通图。一开始我以为只要求出桥的个数，然后在每个桥的地方加一条边就行了，后来发现不是。
例如：
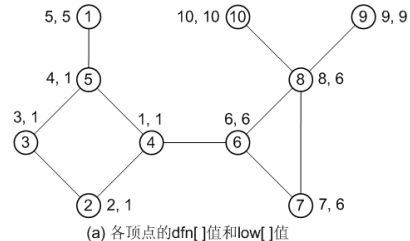这个图中，桥有4条，但实际上只需要在1跟10，10跟9中间加两条边就行了。所以，实际上这个题是先进行缩点，然后求缩点后的图至少增加几条变能够变成双连通图。缩点之后构建成一颗树，所有的边都是桥，根据定理，任意一颗树，要想成为双连通图，则需要增加的边数为（这棵树上所有度数为1的结点的个数+1）/2。
知识点 ：
边双连通图 ： 如果一个无向连通图G没有割边，或者说边连通度λ(G)>1，则称G为边双连通图。因为在这种图中任何一对顶点之间至少存在2条无公共边的路径（允许有公共内部顶点），在删去某条边后，也不会破坏图的连通性。
边双联通分量的定义 ： 一个连通图G如果不是边双连通图，那么它可以包括几个边双连通分量。一个连通图的边双连通分量是该图的极大重连通子图，在边双连通分量中不存在割边。在连通图中，把割边删除，则连通图变成了多个连通分量，每个连通分量就是一个边双连通分量。
#include <stdio.h> #include <string.h> #include <iostream> #include <stdlib.h> using namespace std ; const int maxn = 33333 ; int head[maxn],out[maxn] ,low[maxn],dfn[maxn],vis[maxn] ; int cnt,bcc_clock,m,n ; struct node { int u,v,w,next ; }edge[maxn] ; void addedge(int u,int v) { edge[cnt].u = u ; edge[cnt].v = v ; edge[cnt].next = head[u] ; head[u] = cnt++ ; } void Init() { memset(head,-1,sizeof(head)) ; memset(dfn,0,sizeof(dfn)) ; memset(out,0,sizeof(out)) ; memset(low,0,sizeof(low)) ; memset(vis,0,sizeof(vis)) ; cnt = 0,bcc_clock = 0 ; } void tarjan(int u,int w)//将u与其父亲结点编号传入 { dfn[u] = low[u] = ++bcc_clock ; vis[u] = 1 ; for(int i = head[u] ; i+1 ; i = edge[i].next) { int v = edge[i].v ; if(vis[v] == 1 && w != v) low[u] = min(low[u],dfn[v]) ; if(vis[v] == 0) { tarjan(v,u) ; low[u] = min(low[v],low[u]) ; } } vis[u] = 2 ; } int main() { int n , m; while(~scanf("%d %d",&n,&m)) { Init() ; int x,y ; while(m--) { scanf("%d %d",&x,&y) ; addedge(x,y) ; addedge(y,x) ; } tarjan(1,1) ; for(int i = 1 ; i <= n ; i++) { for(int j = head[i] ; j+1 ; j = edge[j].next) { int v = edge[j].v ; if(low[i] != low[v]) out[low[i]]++ ; } } int countt = 0 ; for(int i = 0 ; i <= n ;i++) if(out[i] == 1) countt++ ; printf("%d\n",(countt+1)/2) ; } return 0 ; }