Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

 

The largest rectangle is shown in the shaded area, which has area = 10 unit.

 

For example,
Given height = [2,1,5,6,2,3],
return 10.

最开始的想法，一层一层往上找，计算包含当前层的最大面积，直到最上层。这个算法时间复杂度很高：

 1 public class Solution {
 2     public int largestRectangleArea(int[] height) {
 3         // Start typing your Java solution below
 4         // DO NOT write main() function
 5         int max = 0;
 6         int maxa = 0;
 7         for(int i = 0; i < height.length; i++){
 8             if(height[i] > max) max = height[i];
 9         }
10         for(int i = 0; i < max; i ++){
11             int cur = 0;
12             for(int j = 0; j < height.length; j ++){
13                 if(height[j] > 0){
14                     height[j] --;
15                     cur ++;
16                 }else{
17                     cur = cur * ( i + 1 );
18                     if(cur > maxa) maxa = cur;
19                     cur = 0;
20                 }
21             }
22         }
23         return maxa;
24     }
25 }

 过不了：

Run Status: Time Limit Exceeded

Last executed input

[0,0,0,0,0,0,0,0,2147483647]
可以看出，可以从两个方面来优化，一是将0的那些数组元素剔除。二是，每次上升的步长不应是1，而是现有元素中最小的那个。
对于第一个，采用array来存放数据，对于第二个动态的得到步长。

错了，不能剔除元素，那样会改变数组结构。

 1 public class Solution {
 2     public int largestRectangleArea(int[] height) {
 3         // Start typing your Java solution below
 4         // DO NOT write main() function
 5         int maxa = 0;
 6         int i = 0;
 7         while(true){
 8             boolean sig = false;
 9             int cur = 0;
10             int maxlvl = 0;
11             int minpath = Integer.MAX_VALUE;
12             for(int j = 0; j < height.length; j ++){
13                 int ht = height[j];
14                 if(ht > 0){
15                     if(minpath > ht)minpath = ht;
16                     cur ++;
17                     sig = true;
18                 }else{
19                     if(cur > maxlvl) maxlvl = cur;
20                     cur = 0;
21                 }
22             }
23             if(cur > maxlvl) maxlvl = cur;
24             if(i == 0) {
25                 i = minpath;
26             }
27             else{
28                 i += minpath;
29             }
30             if(maxlvl * i > maxa) maxa = maxlvl * i;
31             for(int l = 0; l < height.length; l ++){
32                 height[l] -= minpath;
33             }
34             if(sig == false)break;
35         }
36         return maxa;
37     }
38 }

不过这个过不了大测试。还得改进。时间复杂度是O(n2)，n为数组length。

以下摘自水中的鱼：

想了半天，也想不出来O(n)的解法，于是上网google了一下。
如下图所示，从左到右处理直方，i=4时，小于当前栈顶（及直方3），于是在统计完区间[2,3]的最大值以后，消除掉阴影部分，然后把红线部分作为一个大直方插入。因为，无论后面还是前面的直方，都不可能得到比目前栈顶元素更高的高度了。

这就意味着，可以维护一个递增的栈，每次比较栈顶与当前元素。如果当前元素小于栈顶元素，则入站，否则合并现有栈，直至栈顶元素小于当前元素。结尾入站元素0，重复合并一次。

Update: Refactor code 5/7/2013
评论中Zhongwen Ying的code写的比我post的code简洁多了。把他的code format一下集成进来。

1:  int largestRectangleArea(vector<int> &h) {  
2:       stack<int> S;  
3:       h.push_back(0);  
4:       int sum = 0;  
5:       for (int i = 0; i < h.size(); i++) {  
6:            if (S.empty() || h[i] > h[S.top()]) S.push(i);  
7:            else {  
8:                 int tmp = S.top();  
9:                 S.pop();  
10:                 sum = max(sum, h[tmp]*(S.empty()? i : i-S.top()-1));  
11:                 i--;  
12:            }  
13:       }  
14:       return sum;  
15:  }  


很好的解法：转自 http://blog.csdn.net/abcbc/article/details/8943485

具体的题目描述为：

 

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height =[2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area =10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

这道题可以有两个解法。

解法一是穷举法，对于直方图的每一个右边界，穷举所有的左边界。将面积最大的那个值记录下来。时间复杂度为O(n^2). 单纯的穷举在LeetCode上面过大集合时会超时。可以通过选择合适的右边界，做一个剪枝(Pruning)。观察发现当height[k] >= height[k - 1]时，无论左边界是什么值，选择height[k]总会比选择height[k - 1]所形成的面积大。因此，在选择右边界的时候，首先找到一个height[k] < height[k - 1]的k，然后取k - 1作为右边界，穷举所有左边界，找最大面积。

Java代码：

 

// O(n^2) with pruning
public int largestRectangleArea1(int[] height) {
  // Start typing your Java solution below
  // DO NOT write main() function
  int area = 0;
  for (int i = 0; i < height.length; i++) {
    for (int k = i + 1; k < height.length; k++) {
      if (height[k] < height[k - 1]) {
        i = k - 1;
        break;
      } else {
        i = k;
      }
    }
    int lowest = height[i];
    for (int j = i; j >= 0; j--) {
      if (height[j] < lowest) {
        lowest = height[j];
      }
      int currArea = (i - j + 1) * lowest;
      if (currArea > area) {
        area = currArea;
      }
    }
  }
  return area;
}

虽然上面的解法可以过大集合，但是不是最优的方法，下面介绍使用两个栈的优化解法。时间复杂度为O(n).

 

此解法的核心思想为：一次性计算连续递增的区间的最大面积，并且考虑完成这个区间之后，考虑其前、后区间的时候，不会受到任何影响。也就是这个连续递增区间的最小高度大于等于其前、后区间。

这个方法非常巧妙，最好通过一个图来理解：

假设输入直方图为：int[] height = {2,7,5,6,4}.

这个方法运行的时候，当遇到height[2] == 5的时候，发现其比之前一个高度小，则从当前值（5）开始，向左搜索比当前值小的值。当搜索到最左边（2）时，比5小，此时计算在height[0]和height[2]之间的最大面积，注意不包括height[0]和和height[2]。height[1]以红色标出的这个区域就被计算完成。同样的方法，计算出绿色和粉色的面积。

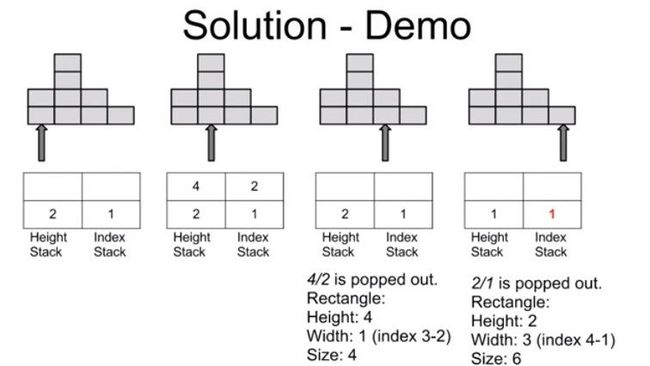
因此这个方法需要使用两个栈。第一个栈为高度栈heightStack，用于记录还没有被计算过的连续递增的序列的值。第二个栈为下标栈indexStack，用于记录高度栈中对应的每一个高度的下标，以计算宽度。

算法具体执行的步骤为：

若heightStack为空或者当前高度大于heightStack栈顶，则当前高度和当前下标分别入站。所以heightStack记录了一个连续递增的序列。

若当前高度小于heightStack栈顶，heightStack和indexStack出栈，直到当前高度大于等于heightStack栈顶。出栈时，同时计算区间所形成的最大面积。注意计算完之后，当前值入栈的时候，其对应的下标应该为最后一个从indexStack出栈的下标。比如height[2]入栈时，其对应下标入栈应该为1，而不是其本身的下标2。如果将其本身下标2入栈，则计算绿色区域的最大面积时，会忽略掉红色区域。

Java代码：

 

// O(n) using two stacks
public int largestRectangleArea(int[] height) {
  // Start typing your Java solution below
  // DO NOT write main() function
  int area = 0;
  java.util.Stack<Integer> heightStack = new java.util.Stack<Integer>();
  java.util.Stack<Integer> indexStack = new java.util.Stack<Integer>();
  for (int i = 0; i < height.length; i++) {
    if (heightStack.empty() || heightStack.peek() <= height[i]) {
      heightStack.push(height[i]);
      indexStack.push(i);
    } else if (heightStack.peek() > height[i]) {
      int j = 0;
      while (!heightStack.empty() && heightStack.peek() > height[i]) {
        j = indexStack.pop();
        int currArea = (i - j) * heightStack.pop();
        if (currArea > area) {
          area = currArea;
        }
      }
      heightStack.push(height[i]);
      indexStack.push(j);
    }
  }
  while (!heightStack.empty()) {
    int currArea = (height.length - indexStack.pop()) * heightStack.pop();
    if (currArea > area) {
      area = currArea;
    }
  }
  return area;
}

更新：

在网上发现另外一个使用一个栈的O(n)解法，代码非常简洁，栈内存储的是高度递增的下标。对于每一个直方图高度，分两种情况。1：当栈空或者当前高度大于栈顶下标所指示的高度时，当前下标入栈。否则，2：当前栈顶出栈，并且用这个下标所指示的高度计算面积。而这个方法为什么只需要一个栈呢？因为当第二种情况时，for循环的循环下标回退，也就让下一次for循环比较当前高度与新的栈顶下标所指示的高度，注意此时的栈顶已经改变由于之前的出栈。

Java代码：

 

// O(n) using one stack
public int largestRectangleArea(int[] height) {
  // Start typing your Java solution below
  // DO NOT write main() function
  int area = 0;
  java.util.Stack<Integer> stack = new java.util.Stack<Integer>();
  for (int i = 0; i < height.length; i++) {
    if (stack.empty() || height[stack.peek()] < height[i]) {
      stack.push(i);
    } else {
      int start = stack.pop();
      int width = stack.empty() ? i : i - stack.peek() - 1;
      area = Math.max(area, height[start] * width);
      i--;
    }
  }
  while (!stack.empty()) {
    int start = stack.pop();
    int width = stack.empty() ? height.length : height.length - stack.peek() - 1;
    area = Math.max(area, height[start] * width);
  }
  return area;
}

 1 public class Solution {
 2     public class Element{
 3         int height;
 4         int index;
 5         public Element(int i, int h){
 6             this.height = h;
 7             this.index = i;
 8         }
 9     }
10     public int largestRectangleArea(int[] height) {
11         // Start typing your Java solution below
12         // DO NOT write main() function
13         if(height == null || height.length == 0) return 0;
14         Stack<Element> st = new Stack<Element>();
15         int max = Integer.MIN_VALUE;
16         for(int i = 0; i < height.length; i ++){
17             if(st.isEmpty() || st.peek().height < height[i]){
18                 st.push(new Element(i, height[i]));
19             }else if(st.peek().height > height[i]){
20                 Element tmp = null;
21                 while(!st.isEmpty() && st.peek().height > height[i]){
22                     tmp = st.pop();
23                     int cur = (i - tmp.index) * tmp.height;
24                     max = cur > max ? cur : max;
25                 }
26                 st.push(new Element(tmp.index, height[i]));
27             }
28         }
29         while(!st.isEmpty()){
30             Element tmp = st.pop();
31             int cur = (height.length - tmp.index) * tmp.height;
32             max = cur > max ? cur : max;
33         }
34         return max;
35     }
36 }