NOIP2002提高组
第一题 均分纸牌
【题目描述】
有 N 堆纸牌,编号分别为 1,2,…, N。每堆上有若干张,但纸牌总数必为 N 的倍数。可以在任一堆上取若于张纸牌,然后移动。
移牌规则为:在编号为 1 堆上取的纸牌,只能移到编号为 2 的堆上;在编号为 N 的堆上取的纸牌,只能移到编号为 N-1 的堆上;其他堆上取的纸牌,可以移到相邻左边或右边的堆上。
现在要求找出一种移动方法,用最少的移动次数使每堆上纸牌数都一样多。
例如 N=4,4 堆纸牌数分别为:
① 9 ② 8 ③ 17 ④ 6
移动3次可达到目的:
从 ③ 取 4 张牌放到 ④ (9 8 13 10) -> 从 ③ 取 3 张牌放到 ②(9 11 10 10)-> 从 ② 取 1 张牌放到①(10 10 10 10)。
【输入格式】
第一行,N(N 堆纸牌,1 <= N <= 100)
第二行,A1 A2 … An (N 堆纸牌,每堆纸牌初始数,l<= Ai <=10000)
【输出格式】
一个数,所有堆均达到相等时的最少移动次数。
【样例输入】
4
9 8 17 6
【样例输出】
3
【分析】
计算出堆的牌数。从左向右,如果当前堆比最终值大,把多出来的加到下一堆。如果少,从下一堆取。不用考虑下一堆不够用。
第二题 字串变换
忽略。
第三题 自由落体
【题目描述】
在高为 H 的天花板上有 n 个小球,体积不计,位置分别为 0,1,2,….n-1。在地面上有一个小车(长为 L,高为 K,距原点距离为 S1)。已知小球下落距离计算公式为 d=1/2*g*(t^2),其中 g=10,t 为下落时间。地面上的小车以速度 V 前进。
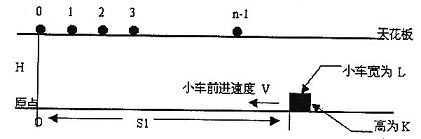
有小球同时开始运动,当小球距小车的距离 <= 0.00001 时,即认为小球被小车接受(小球落到地面后不能被接受)。
请你计算出小车能接受到多少个小球。
【输入格式】
一行,H,S1,V,L,K,n (l<=H,S1,V,L,K,n <=100000)
【输出格式】
一个数,小车能接受到的小球个数。
【样例输入】
5.0 9.0 5.0 2.5 1.8 5
【样例输出】
1
【分析】
模拟。
第四题 矩阵覆盖
【题目描述】
在平面上有 n 个点(n <= 50),每个点用一对整数坐标表示。例如:当 n=4 时,4个点的坐标分另为:p1(1,1),p2(2,2),p3(3,6),P4(0,7),见图一。
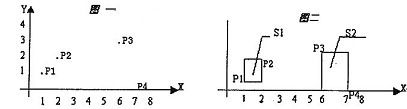
用 k 个矩形(1<=k<=4)全部覆盖,矩形的边平行于坐标轴。当 k=2 时,可用如图二的两个矩形 sl,s2 覆盖,s1,s2 面积和为 4。问题是当 n 个点坐标和 k 给出后,怎样才能使得覆盖所有点的 k 个矩形的面积之和为最小呢。约定:覆盖一个点的矩形面积为 0;覆盖平行于坐标轴直线上点的矩形面积也为0。各个矩形必须完全分开(边线与顶点也都不能重合)。
【输入格式】
第一行n和k
下面n行为每一个矩形的坐标(0<=xi,yi<=500)
【输出格式】
一个整数,即满足条件的最小的矩形面积之和。
【样例输入】
4 2
1 1
2 2
3 6
0 7
【样例输出】
4
【分析】
本题目本人写的方法有问题。但是碰巧AC。想看正解的请无视这个题解。
动归。
首先将所有的点从左向右排序。
f[i][j]代表前i个点用了j个矩形。f[i][j] = min{f[k][j – 1] + s[k + 1][i]}。其中s[i][j]代表第i个点到第j个点放入一个矩形所需要的最小面积。
代码
第一题
#include <stdio.h>
#define MAXN 110
int tot,ave,ans,n;
int a[MAXN];
int main() {
scanf("%d",&n);
for (int i = 1;i <= n;++i) {
scanf("%d",&a[i]);
tot += a[i];
}
ave = tot / n;
for (int i = 1;i <= n;++i)
if (a[i] < ave) {
tot = ave - a[i];
a[i] = ave;
++ans;
a[i + 1] -= tot;
} else {
if (a[i] > ave) {
tot = a[i] - ave;
++ans;
a[i + 1] += tot;
}
}
printf("%d\n",ans);
return 0;
}
第三题
var n,g,s1,s2,s0:integer; h,s,v,l,k,t00,SEVE,t01,t1,t2,d1,d2:real; begin readln(h,s,v,l,k,n); g:=10; s0:=0; t00:=sqrt(2*h/g); t01:=sqrt(2*(h-k)/g); s1:=trunc(s-t00*v); s2:=trunc(s-t01*v+l); if s1<0 then s1:=0; if s2<0 then s2:=0; if (n-1<s1)then s0:=0 else if(n-1<s2) then s0:=n-s1 else s0:=s2-s1; writeln(s0); end.
第四题
#include <stdio.h>
#include <stdlib.h>
#define MAXN 60
#define MAXINT 1000010
struct node {
int x,y;
} a[MAXN];
int f[MAXN][5],s[MAXN][MAXN];
int n,m,high,low;
int cmp(const void *a,const void *b) {
node c = *(node *)a,d = *(node *)b;
if (c.x < d.x)
return -1;
if (c.x > d.x)
return 1;
if (c.y < d.y)
return -1;
if (c.y > d.y)
return 1;
return 0;
}
int main() {
scanf("%d%d",&n,&m);
for (int i = 1;i <= n;++i)
scanf("%d%d",&a[i].y,&a[i].x);
qsort(a + 1,n,sizeof(node),cmp);
for (int i = 1;i <= n;++i) {
high = a[i].y;
low = a[i].y;
for (int j = i;j <= n;++j) {
if (a[j].y > high)
high = a[j].y;
if (a[j].y < low)
low = a[j].y;
s[i][j] = (high - low) * (a[j].x - a[i].x);
}
}
for (int i = 1;i <= n;++i) {
f[i][1] = s[1][i];
for (int k = 2;k <= m;++k) {
f[i][k] = MAXINT;
for (int j = k - 1;j < i;++j)
if (f[j][k - 1] + s[j + 1][i] < f[i][k])
f[i][k] = f[j][k - 1] + s[j + 1][i];
}
}
printf("%d\n",f[n][m]);
return 0;
}