CRC(Cyclic Redundancy Check)循环冗余校验码与海明码的计算题
(17)采用CRC进行差错校验,生成多项式为G(X)=X4+X+1,信息码字为10111,则计算出的CRC校验码是 (17) 。
A.0000 B.0100 C.0010 D.1100
试题解析:
答案:(17)D
CRC(Cyclic Redundancy Check)循环冗余校验码 是常用的校验码,在早期的通信中运用广泛,因为早期的通信技术不够可靠(不可靠性的来源是通信技术决定的,比如电磁波通信时受雷电等因素的影响),不可靠的通信就会带来‘确认信息’的困惑,书上提到红军和蓝军通信联合进攻山下的敌军的例子,第一天红军发了条信息要蓝军第二天一起进攻,蓝军收到之后,发一条确认信息,但是蓝军担心的是‘确认信息’如果也不可靠而没有成功到达红军那里,那自己不是很危险?于是红军再发一条‘对确认的确认信息’,但同样的问题还是不能解决,红军仍然不敢冒然行动。 对通信的可靠性检查就需要‘校验’,校验是从数据本身进行检查,它依靠某种数学上约定的形式进行检查,校验的结果是可靠或不可靠,如果可靠就对数据进行处理,如果不可靠,就丢弃重发或者进行修复。 CRC码是由两部分组成,前部分是信息码,就是需要校验的信息,后部分是校验码,如果CRC码共长n个bit,信息码长k个bit,就称为(n,k)码。 它的编码规则是: 1、首先将原信息码(kbit)左移r位(k+r=n) 2、运用一个生成多项式g(x)(也可看成二进制数)用模2除上面的式子,得到的余数就是校验码。 非常简单,要说明的:模2除就是在除的过程中用模2加,模2加实际上就是我们熟悉的异或运算,就是加法不考虑进位,公式是: 0+0=1+1=0,1+0=0+1=1 即‘异’则真,‘非异’则假。 由此得到定理:a+b+b=a 也就是‘模2减’和‘模2加’直值表完全相同。 有了加减法就可以用来定义模2除法,于是就可以用生成多项式g(x)生成CRC校验码。 例如: g(x)=x4+x3+x2+1,(7,3)码,信息码110产生的CRC码就是: 101 11101 | 110,0000 111 01 1 0100 1 1101 1001 余数是1001,所以CRC码是110,1001 标准的CRC码是,CRC-CCITT和CRC-16,它们的生成多项式是: CRC-CCITT=x16+x12+x5+1 CRC-16=x16+x15+x2+1
一、CRC编码
1、已知多项式和原报文,求CRC编码,如:使用多项式G(x)=x^5 + x^4 + x +1,对报文10100110进行CRC编码,则编码后的报文是什么?
方法与步骤:
步骤1:对报文10100110,在末尾添加所给多项式的最高次阶个0,如本题为x^5,则添加5个0,变为:1010011000000。
步骤2:由多项式G(x)=x^5 + x^4 + x +1,得其阶数为1的二进制编码为:110011。
步骤3:步骤1中求得的1010011000000对步骤2中求得的110011进行模二除法,所得到的余数即为校验码,把校验码添加在原报文尾部即为所求的编码报文1010011011000,具体如下:
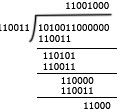
2.已知道接收到的CRC编码,求原编码或判断是否出错,如:已知G(x)=x^5 + x^4 + x +1,接收的为1010011011001,问是否出错?
步骤一:由多项式G(x)=x^5 + x^4 + x +1,得其阶数为1的二进制编码为:110011。
x +1,得其阶数为1的二进制编码为:110011。
步骤二:用接收的报文1010011011001对步骤一的110011进行模二除法,看余数是否为0,如为0则正确,如不为0,则出错,计算余数为1,则出错。如下图:
二、海明码
1.求海明码,如:求1011海明码。
步骤一:求校验码位数r,公式为:2^r ≥r+k+1的最小r。题目中为2^3≥3+4+1,所以取r=3,即校验码为3位。
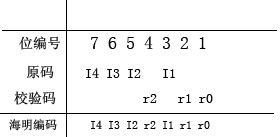
步骤二:画图,并把原码的位编号写成2的指数求和的方式,其中位编号长度为原码和校验码个数之和,从1开始。校验码插在2的阶码次方的位编号下,且阶小于r。如下:
原码的位编号写成2的指数求和:
7=2^2+2^1+2^0;
6=2^2+2^1;
5=2^2+2^0;
3=2^1+2^0;
步骤三:求校验位,即每个校验位的值为步骤二中“原码的位编号写成2的指数求和”式子中相应2的阶出现的位编号下原码的值异或。即:
r0=I4异或I2异或I1=1; (2^0次出现在7,5,3位,其对应的值为I4,I2,I1)
r1=I4异或I3异或I1=0; (2^1次出现在7,6,3位,其对应的值为I4,I3,I1)
r2=I4异或I3异或I2=0; (2^0次出现在7,6,5位,其对应的值为I4,I3,I2)
把r0,r1,r2带入海明码,得所求的海明码为:1010101
2.已知海明码,求原码或判断是否出错并改正错位,如:信息位8位的海明码,接收110010100000时,判断是否出错,并求出发送端信息位。
步骤一:求校验码位数r,公式为:2^r ≥r+k+1的最小r。题目中为2^4≥4+8+1,所以取k=4,即校验码为4位。
步骤二:根据作图,求得信息位编码和发过来的校验码记为r,并由原编码从新计算出新的校验码与发来的校验码r进行异或运算,具体如下:
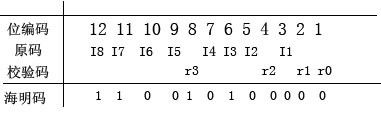
得到,原码11000100,发送来的校验码r为1000
再根据求R,把原码的位编号写成2的指数求和:
12=2^3+2^2;
11=2^3+2^1+2^0;
10=2^3+2^0;
9=2^3+2^0;
7=2^2+2^1+2^0;
6=2^2+2^1;
5=2^2+2^0;
3=2^1+2^0;
求得:
S3=r3异或(I8异或I7异或I6异或I5)
S2=r2异或(I8异或I4异或I3异或I2)
S1=r1异或(I7异或I6异或I4异或I3异或I1)
S0=r0异或(I7异或I5异或I4异或I2异或I1)
S3S2S1S0,其十进制为0,表示没出错,如果不为零,则其十进制数即为出错的位。
本题S3S2S1S0=1001,十进制为9,即第九位出错。改过来既为:11010100
注:不管用海明还是CRC编码,如果不是有必要或学密码学,不用想办法搞清原理,就拿它当像勾股定理一样使用就ok,否则,对一般来讲,的确有点痛苦。