SPOJ AMR10E Stocks Prediction --二分求和+矩阵快速幂

题意：给一个递推式S(n) = a1*S(n-1)+...+aR*S(n-R),要求S(k)+S(2k)+...+S(nk)的值。

分析：看到n的大小和递推式，容易想到矩阵快速幂。但是如何转化呢？

首先看到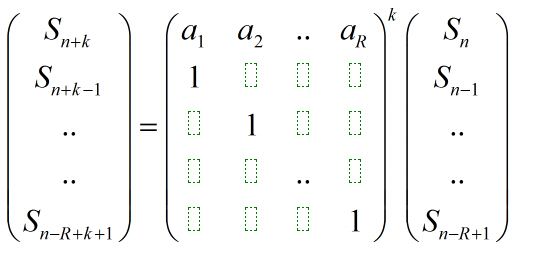

我们用A表示上面的递推式中的R*R的那个矩阵，那么对于前面那个向量，每次乘上A^k之后都会变成(S(n + k)...)
那么对于初始的向量( S(R) S(R - 1) ... S(1) ) 如果这个向量当中包括 S(k) 我们可以直接对于每次要算的 S( i * k) 求和
也就是说这个向量乘上( I + A^k + (A^k)^2 + (A^k)^3 + ... + (A^k)^(N - 1))之后对应的 S(k) 所在的那个位置就变成了要求的和
而对于那个矩阵型的等比数列求和可以直接用二分求和(常用的技巧)，这样就可以在限制的时间内完成计算了  （Gatevin）

代码：

#include <iostream>

#include <cstdio>

#include <cstring>

#include <cmath>

#include <algorithm>

#define Mod 1000000007

#define ll long long

using namespace std;

#define N 100007



ll s[11],a[11];

ll n;

int r;



struct Matrix

{

    ll m[11][11];

    Matrix()

    {

        memset(m,0,sizeof(m));

        for(int i=1;i<=10;i++)

            m[i][i] = 1;

    }

};



Matrix Mul(Matrix a,Matrix b)

{

    Matrix res;

    int i,j,k;

    for(i=1;i<=r;i++)

    {

        for(j=1;j<=r;j++)

        {

            res.m[i][j] = 0;

            for(k=1;k<=r;k++)

                res.m[i][j] = (res.m[i][j]+(a.m[i][k]*b.m[k][j]%Mod))%Mod;

        }

    }

    return res;

}



Matrix add(Matrix a,Matrix b)

{

    Matrix res;

    memset(res.m,0,sizeof(res.m));

    int i,j;

    for(i=1;i<=r;i++)

        for(j=1;j<=r;j++)

            res.m[i][j] = (a.m[i][j]+b.m[i][j])%Mod;

    return res;

}



Matrix fastm(Matrix a,ll b)

{

    Matrix res;

    while(b)

    {

        if(b&1LL)

            res = Mul(res,a);

        a = Mul(a,a);

        b >>= 1;

    }

    return res;

}



Matrix getsum(Matrix a,ll b)     //二分求矩阵等比数列和

{

    Matrix I;  //单位阵

    if(b == 1LL)

        return I;

    if(b&1LL)

        return add(getsum(a,b-1LL),fastm(a,b-1LL));

    else

        return Mul(getsum(a,b/2LL),add(I,fastm(a,b/2LL)));  // (I+A^k+...+A^(n/2)k)*(I+A^(n/2)k)

}



int main()

{

    int t,i,j,k;

    scanf("%d",&t);

    while(t--)

    {

        scanf("%lld%d%d",&n,&r,&k);

        for(i=1;i<=r;i++)

            scanf("%lld",&s[i]);

        for(i=1;i<=r;i++)

            scanf("%lld",&a[i]);

        Matrix A;

        memset(A.m,0,sizeof(A.m));

        for(i=1;i<=r;i++)  //构造矩阵

        {

            A.m[1][i] = a[i];

            if(i < r)

                A.m[i+1][i] = 1;

        }

        //求 I+A^k+A^(2k)+...+A^(n-1)k

        Matrix base = fastm(A,k);

        Matrix ans = getsum(base,n);

        ll res = 0;

        if(k <= r)    //第k项在给出的数内

        {

            for(i=1;i<=r;i++)

                res = (res + (s[i]*ans.m[r-k+1][r-i+1]%Mod))%Mod;

            printf("%lld\n",res%Mod);

        }

        else      //否则先算出s[r+1]...s[k]

        {

            for(i=r+1;i<=k;i++)

            {

                s[i] = 0;

                for(j=1;j<=r;j++)

                    s[i] = (s[i]+s[i-j]*a[j]%Mod)%Mod;

            }

            for(i=1;i<=r;i++)

                res = (res + (s[k-i+1]*ans.m[1][i])%Mod)%Mod;

            printf("%lld\n",res%Mod);

        }

    }

    return 0;

}

View Code