bellman－ford算法

给定图G(V, E)（其中V、E分别为图G的顶点集与边集），源点s，

 

• 数组Distant[i]记录从源点s到顶点i的路径长度，初始化数组Distant[n]为, Distant[s]为0；
•  
  以下操作循环执行至多n-1次，n为顶点数：
  对于每一条边e(u, v)，如果Distant[u] + w(u, v) < Distant[v]，则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值；
  若上述操作没有对Distant进行更新，说明最短路径已经查找完毕，或者部分点不可达，跳出循环。否则执行下次循环；
• 为了检测图中是否存在负环路，即权值之和小于0的环路。对于每一条边e(u, v)，如果存在Distant[u] + w(u, v) < Distant[v]的边，则图中存在负环路，即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。

可知，Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).

首先介绍一下松弛计算。如下图：

 

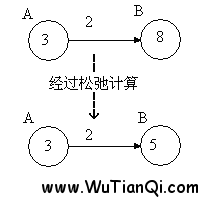
松弛计算之前，点B的值是8，但是点A的值加上边上的权重2，得到5，比点B的值（8）小，所以，点B的值减小为5。这个过程的意义是，找到了一条通向B点更短的路线，且该路线是先经过点A，然后通过权重为2的边，到达点B。
当然，如果出现一下情况

 

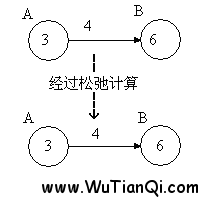
则不会修改点B的值，因为3＋4>6。
 
Bellman－Ford算法可以大致分为三个部分
第一，初始化所有点。每一个点保存一个值，表示从原点到达这个点的距离，将原点的值设为0，其它的点的值设为无穷大（表示不可达）。
第二，进行循环，循环下标为从1到n－1（n等于图中点的个数）。在循环内部，遍历所有的边，进行松弛计算。
第三，遍历途中所有的边（edge（u，v）），判断是否存在这样情况：
d（v） > d (u) + w(u,v)
则返回false，表示途中存在从源点可达的权为负的回路。
 
之所以需要第三部分的原因，是因为，如果存在从源点可达的权为负的回路。则 应为无法收敛而导致不能求出最短路径。
考虑如下的图：
 

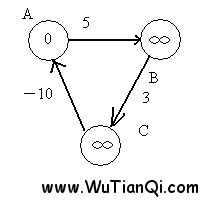
经过第一次遍历后，点B的值变为5，点C的值变为8，这时，注意权重为－10的边，这条边的存在，导致点A的值变为－2。（8＋ －10＝－2）
 
 

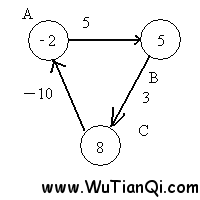
第二次遍历后，点B的值变为3，点C变为6，点A变为－4。正是因为有一条负边在回路中，导致每次遍历后，各个点的值不断变小。
 
在回过来看一下bellman－ford算法的第三部分，遍历所有边，检查是否存在d（v） > d (u) + w(u,v)。因为第二部分循环的次数是定长的，所以如果存在无法收敛的情况，则肯定能够在第三部分中检查出来。比如
 

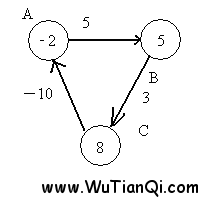
此时，点A的值为－2，点B的值为5，边AB的权重为5，5 > -2 + 5. 检查出来这条边没有收敛。
 
所以，Bellman－Ford算法可以解决图中有权为负数的边的单源最短路径问。

考虑：为什么要循环V-1次？
答：因为最短路径肯定是个简单路径，不可能包含回路的，
如果包含回路，且回路的权值和为正的，那么去掉这个回路，可以得到更短的路径
如果回路的权值是负的，那么肯定没有解了

图有n个点，又不能有回路
所以最短路径最多n-1边

又因为每次循环，至少relax一边
所以最多n-1次就行了

 1 #include <iostream>

 2 using namespace std;

 3 const int maxnum = 100;

 4 const int maxint = 99999;

 5 

 6 // 边，

 7 typedef struct Edge{

 8     int u, v;    // 起点，重点

 9     int weight;  // 边的权值

10 }Edge;

11 

12 Edge edge[maxnum];     // 保存边的值

13 int  dist[maxnum];     // 结点到源点最小距离

14 

15 int nodenum, edgenum, source;    // 结点数，边数，源点

16 

17 // 初始化图

18 void init()

19 {

20     // 输入结点数，边数，源点

21     cin >> nodenum >> edgenum >> source;

22     for(int i=1; i<=nodenum; ++i)

23         dist[i] = maxint;

24     dist[source] = 0;

25     for(int i=1; i<=edgenum; ++i)

26     {

27         cin >> edge[i].u >> edge[i].v >> edge[i].weight;

28         if(edge[i].u == source)          //注意这里设置初始情况

29             dist[edge[i].v] = edge[i].weight;

30     }

31 }

32 

33 // 松弛计算

34 void relax(int u, int v, int weight)

35 {

36     if(dist[v] > dist[u] + weight)

37         dist[v] = dist[u] + weight;

38 }

39 

40 bool Bellman_Ford()

41 {

42     for(int i=1; i<=nodenum-1; ++i)

43         for(int j=1; j<=edgenum; ++j)

44             relax(edge[j].u, edge[j].v, edge[j].weight);

45     bool flag = 1;

46     // 判断是否有负环路

47     for(int i=1; i<=edgenum; ++i)

48         if(dist[edge[i].v] > dist[edge[i].u] + edge[i].weight)

49         {

50             flag = 0;

51             break;

52         }

53     return flag;

54 }

55 int main()

56 {

57     //freopen("input3.txt", "r", stdin);

58     init();

59     if(Bellman_Ford())

60         for(int i = 1 ;i <= nodenum; i++)

61             cout << dist[i] << endl;

62     return 0;

63 }

View Code