堆排序

堆的定义如下：

n个元素的序列{k0,k1,...,ki,…,k(n-1)}当且仅当满足下关系时，称之为堆。

"ki<=k(2i),ki<=k(2i+1);或ki>=k(2i),ki>=k(2i+1).（i=1,2,…,[n/2])"

若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，

若完全二叉树中每一个节点的值都大于或等于任意一个子节点的值（如果有的话），称之为大顶堆。

若完全二叉树中每一个节点的值都小于或等于任意一个子节点的值（如果有的话），称之为小顶堆。

由此，若序列{k0,k1,…,k(n-1)}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。

倘若给堆中每一个节点都赋予一个整数值标签，根节点被标记为0，对于每一个标记为i的节点，其左子节点（若存在的话）被标记为2*i+1，其右子节点（若存在的话）被标记为2*i+2，对于一个标记为i的非根节点，其父节点被标记为（i-1）/2。使用这个标记，我们能够将堆存储在数组中，节点存储在数据中的位置就使其标签。

堆排序示例：

规则：

1.初始化i=0，先后查看节点i的左子节点2*i+1、右子节点2*i+2，如果发现违反了堆的定义，则交换2个节点的值（编号只跟位置有关，也就是数组中的下标），置i=0

2.如果没有发现违反堆的定义，则置i=i+1，返回步骤1

3.当i==n的时候，将0号位置上的元素放置到n号位置上，置i=0，置n=n-1，返回步骤1，对位置为[0, n]范围内的元素重复上述操作

示意图如下：数组中的值依次是17,8,45,84,2,94，这次排序的最终结果是把最大的94放到了序列末尾

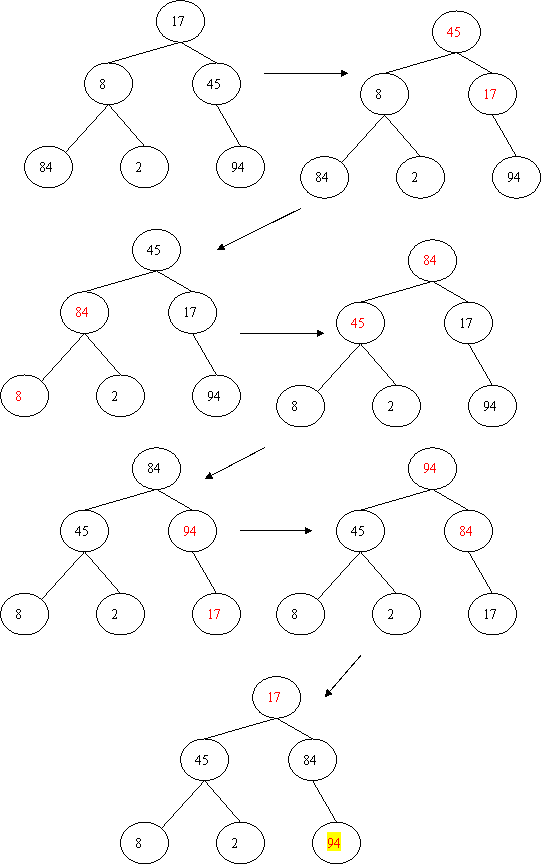
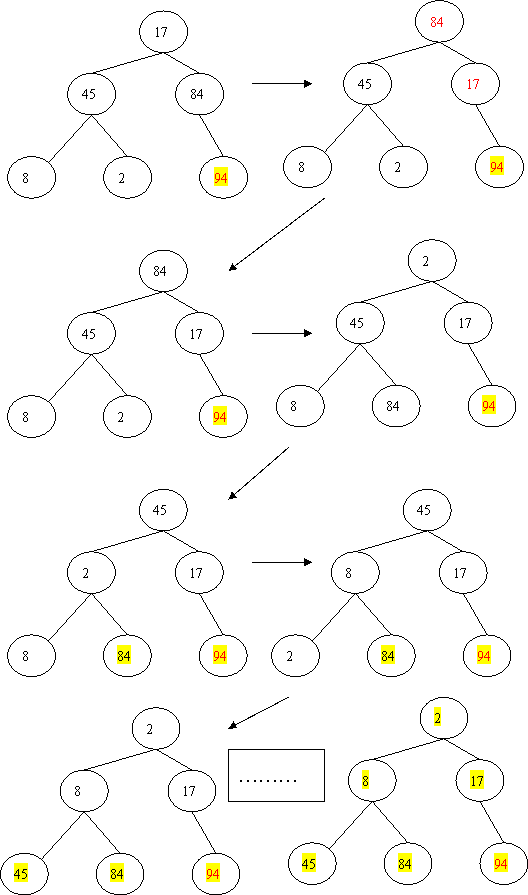
下面是剩下的元素的排序过程：

代码如下：

 1 package sorts;

 2 

 3 import java.util.Arrays;

 4 

 5 public class  Heap<T extends Comparable<T>> // 小顶堆，也就是说小的数据在堆顶部

 6 {

 7     // index starts from 0

 8     private int parent(int index) {

 9         if (index%2==0) {

10             return ( index / 2 ) - 1;

11         } else {

12             return index / 2;

13         }

14     }

15     

16     private int lchild(int index) {

17         return index * 2 + 1;

18     }

19     

20     private int rchild(int index) {

21         return index * 2 + 2;

22     }

23     

24     

25     public void heap_sort(T[] a,int n){

26         if(n>0){

27             init_sort(a,n);//初始化堆，找出最大的放在堆顶

28             swap(a, 0, n);

29             heap_sort(a, n-1); // recursively

30         }

31     }

32     

33     private void swap(T[] a, int index1, int index2) {

34         T temp = a[index1];

35         a[index1] = a[index2];

36         a[index2] = temp;

37     }

38 

39     private void init_sort(T[] a,int n){        

40         int m=(n+1)/2;    

41         for(int i=0;i<m;i++){

42             boolean flag=min_heapify(a,n,i);

43             //如果孩子之间有交换，就要重新开始

44             if(flag){

45                 i=-1;

46             }

47         }

48     }

49     

50     //返回一个标记，如果有根与孩子交换就要重新从顶根开始查找不满足最大堆树结构

51     private boolean min_heapify(T a[],int n,int i){

52         int l_child=lchild(i);//左孩子

53         int r_child=rchild(i);//右孩子

54         if(r_child>n){           //判断是否有右孩子，没有的话直接比较，小于右孩子则交换

55             if(a[i].compareTo(a[l_child])<0){

56                 swap(a, i, l_child);

57                 return true;

58             }else{

59                 return false;

60             }

61         }

62         //在根与两个孩子之间找出最大的那个值进行交换

63         if(a[i].compareTo(a[l_child])<0){

64             if(a[l_child].compareTo(a[r_child])>0){

65                 //交换根与左孩子的值

66                 swap(a, i, l_child);

67                 return true;

68             }else{

69                 //交换根与右孩子的值

70                 swap(a, i, r_child);

71                 return true;

72             }

73         }else if(a[i].compareTo(a[r_child])<0){

74             //交换根与右孩子的值

75             swap(a, i, r_child);

76             return true;

77         }

78         return false;

79             

80     }

81     public static void main(String[] args) 

82     {

83         Heap h = new Heap();

84         Integer [] a={17,8,45,84,2,94};

85         h.heap_sort(a,a.length-1);

86         System.out.println(Arrays.toString(a));

87     }

88 }