【Golang】手搓RSA加密 大素数生成（完整代码）

---

完整系列代码已上传至：

github仓库地址 自取 by preciouswxe/GoCipher

各位大佬不吝star⭐鸣谢

---

一 项目结构

二 所有函数功能和源码

rsa.go内的函数

一、Calculate_n 函数

功能：计算 n = p * q，p 和 q 为 RSA 算法中的大素数。
实现：
创建 big.Int 类型的 result 存储结果。
用 Mul 方法计算 HugeP 和 HugeQ 的乘积存入 result。
打印结果并返回。

二、Calculate_varphi 函数

功能：计算 varphi(n) = (p - 1) * (q - 1)。
实现：
先创建值为 1 的 big.Int 常量 one。
分别计算 p - 1 和 q - 1。
相乘得到结果并返回。

三、Extended_gcd 函数

功能：实现扩展欧几里得算法，求 a * x + b * y = gcd(a, b) 的 gcd、x、y。
实现：
当 b == 0，返回 a、1、0。
递归调用自身，根据递归结果计算当前 x 和 y 并返回。

四、GetPrivate_d 函数

功能：计算私钥 d，即 e 对 varphi(n) 的模反元素。
实现：
初始化 x 和 y，调用 Extended_gcd 计算。
检查 gcd 是否为 1，若不是则报错。
确保 x 为正且小于 varphi(n)。
验证 ed ≡ 1 mod φ(n)，满足则返回 x，否则报错。

五、stringToIntArray 函数

功能：将字符串转换为 big.Int 数组，并找到最大数字对应的 big.Int。
实现：
遍历字符串，将每个字符的 ASCII 码转换为 big.Int 存入数组 mArray。
比较找到最大的 big.Int，最后返回数组和最大的 big.Int。

六、Encrypt 函数

功能：使用公钥 (e, n) 对字符串加密。
实现：
将字符串转换为 big.Int 数组 mArray。
对每个 m，用加密公式 c = m^e mod n 计算密文，存入 cipherArray 并返回。

七、Decrypt 函数

功能：使用私钥 (d, n) 对密文解密。
实现：
对密文数组每个 c，用解密公式 m = c^d mod n 计算明文数字，转换为字符拼接成字符串返回。

rsa.go代码

package main

import (
	"fmt"
	"math/big"
)

func Calculate_n(HugeP *big.Int, HugeQ *big.Int) *big.Int {
	result := new(big.Int)
	// 使用Mul方法进行乘法运算，将num1和num2相乘的结果存储在result变量中
	result.Mul(HugeP, HugeQ)
	fmt.Println("计算n=p*q结果为:", result)
	return result
}

func Calculate_varphi(HugeP *big.Int, HugeQ *big.Int) *big.Int {
	one := big.NewInt(1)
	// 计算p - 1
	pSubOne := new(big.Int).Sub(HugeP, one)
	// 计算q - 1
	qSubOne := new(big.Int).Sub(HugeQ, one)

	result := new(big.Int)
	// 计算(p - 1) * (q - 1)
	result.Mul(pSubOne, qSubOne)

	return result
}

// 扩展欧几里得蒜法 ，返回 gcd, x, y 使得 a * x + b * y = gcd
func Extended_gcd(a, b, x, y *big.Int) (*big.Int, *big.Int, *big.Int) {
	// 基本情况，如果 b == 0，则返回 a 和 1, 0
	if b.Cmp(big.NewInt(0)) == 0 {
		return a, big.NewInt(1), big.NewInt(0)
	}

	// 递归调用
	gcd, x1, y1 := Extended_gcd(b, new(big.Int).Mod(a, b), x, y)

	// 计算当前的 x 和 y
	xResult := y1
	yResult := new(big.Int).Sub(x1, new(big.Int).Mul(new(big.Int).Div(a, b), y1))

	// 打印当前的 gcd 和 x, y
	fmt.Println("本轮gcd=", gcd, " x=", xResult, " y=", yResult)

	return gcd, xResult, yResult
}

// 计算私钥 d，计算 e 对于 φ(n) 的模反元素 d
func GetPrivate_d(e, varphi *big.Int) (*big.Int, error) {
	fmt.Println("传入的参数e=", e, " , varphi=", varphi)

	// 初始化x和yds
	x := big.NewInt(1)
	y := big.NewInt(0)

	gcd, x, y := Extended_gcd(e, varphi, x, y)
	if gcd.Cmp(big.NewInt(1)) != 0 {
		return nil, fmt.Errorf("e和varphi不互质，无法计算私钥！")
	}

	fmt.Println("扩展欧几里得算法结果：gcd = ", gcd, ", x = ", x, " y = ", y)

	// 确保结果为正
	if x.Cmp(big.NewInt(0)) < 0 {
		x.Add(x, varphi) // 如果 x 是负数，转为正数，通过加上 varphi (n = p * q)
		fmt.Println("x 计算为负数，正在加上 varphi 后为：", x)
	}

	// 确保私钥 d 小于 varphi(n)
	if x.Cmp(varphi) >= 0 {
		x.Sub(x, varphi)
	}

	// 验证 ed ≡ 1 mod φ(n)
	ed := new(big.Int).Mul(e, x)
	ed.Mod(ed, varphi)
	if ed.Cmp(big.NewInt(1)) == 0 {
		fmt.Println("公钥 e 和 私钥 d 满足 ed ≡ 1 mod φ(n)")
	} else {
		fmt.Println("公钥 e 和 私钥 d 不满足 ed ≡ 1 mod φ(n)")
		return nil, fmt.Errorf("ed ≡ 1 mod φ(n) 不成立")
	}

	fmt.Println("最终计算出的私钥 d = ", x)

	return x, nil
}

// 将字符串转化为数字
func stringToIntArray(input string) ([]*big.Int, *big.Int) {
	var mArray []*big.Int
	var maxDigitLen int64 = 0
	for _, char := range input {
		// 计算每个字符的ASCII码值
		m := big.NewInt(int64(char))
		mArray = append(mArray, m)
		// 寻找最大值来判断n的大小
		if m.Cmp(big.NewInt(maxDigitLen)) > 0 {
			maxDigitLen = m.Int64()
		}
	}
	return mArray, big.NewInt(maxDigitLen)
}

// 加密函数
func Encrypt(e, n *big.Int, input string) ([]*big.Int, error) {
	mArray, _ := stringToIntArray(input)
	var cipherArray []*big.Int
	for _, m := range mArray {
		// 加密公式 c = m^e mod n
		c := new(big.Int).Exp(m, e, n)
		cipherArray = append(cipherArray, c)
	}
	return cipherArray, nil
}

// 解密函数
func Decrypt(d, n *big.Int, cipherArray []*big.Int) (string, error) {
	var decryptedMessage string
	for _, c := range cipherArray {
		// 解密公式 m = c^d mod n
		m := new(big.Int).Exp(c, d, n)
		decryptedMessage += string(m.Int64())
	}
	return decryptedMessage, nil
}

---

millerabin.go内的函数

八、fmod 函数（费马素性检验辅助函数）

功能：基于费马小定理判断一个数是否可能为素数。
实现：计算 (p ^ (a - 1)) % a 是否等于 1，是则返回 true，否则返回 false。

九、MillerRabbin 函数（米勒 - 拉宾素性检验）

功能：对一个数进行米勒 - 拉宾素性检验，判断其是否可能为素数。
实现：
设置循环进行多次检验。

生成随机数 n，调用 fmod 函数检验，若不通过则返回 false，全部通过则返回 true。

十、GenerateBigRange 函数

功能：生成一个指定长度的大整数范围。
实现：根据传入的长度 n，创建一个值为 10 的 big.Int，并计算其 n 次方作为范围返回。

十一、GenerateBigPrimeP 函数

功能：生成一个大素数。
实现：
先调用 GenerateBigRange 得到一个大整数范围。
使用随机数生成器在范围内生成随机数 p。
用 MillerRabbin 函数检验，若不是素数则重新生成，直到得到素数并返回。

millerabin.go代码

package main

import (
	"math/big"
	"math/rand"
	"time"
)

// 1.费马
// 如果a是素数，则(p ^ (a - 1)) % a恒等于1
func fmod(a *big.Int, p int64) bool {
	one, _ := new(big.Int).SetString("1", 10)
	a_ := new(big.Int).Sub(a, one)
	result := new(big.Int).Exp(new(big.Int).SetInt64(p), a_, a)
	if result.String() != "1" {
		return false //此时出错 返回false 结果必须要为1
	}
	return true
}
package main

import (
	"math/big"
	"math/rand"
	"time"
)

// 1.费马
// 如果a是素数，则(p ^ (a - 1)) % a恒等于1
func fmod(a *big.Int, p int64) bool {
	one, _ := new(big.Int).SetString("1", 10)
	a_ := new(big.Int).Sub(a, one)
	result := new(big.Int).Exp(new(big.Int).SetInt64(p), a_, a)
	if result.String() != "1" {
		return false //此时出错 返回false 结果必须要为1
	}
	return true
}

// 2. MillerRabbin 素性检验
func MillerRabbin(a *big.Int) bool {
	p := new(big.Int).Set(a)

	// 1. 将 p-1 拆分为 2^s * d
	d := new(big.Int).Sub(p, big.NewInt(1))
	s := int64(0)
	for d.Bit(0) == 0 {
		s++
		d.Div(d, big.NewInt(2)) // d 被 2 除尽，直到 d 变为奇数
	}

	rand.Seed(time.Now().UnixNano())

	// 2. 进行 100 次检验
	for i := 0; i < 100; i++ {
		// 随机选择基数 a，满足 1 < a < p-1
		n := rand.Int63()
		if new(big.Int).SetInt64(n).Cmp(p) >= 0 || n <= 1 {
			n = rand.Int63n(p.Int64()-1) + 1
		}
		a := new(big.Int).SetInt64(n)

		// 3. 计算 a^d % p 结果儿是不是1和 p-1 是就通过~
		x := new(big.Int).Exp(a, d, p)
		if x.Cmp(big.NewInt(1)) == 0 || x.Cmp(new(big.Int).Sub(p, big.NewInt(1))) == 0 {
			continue // 该次检验通过，继续测试下一个基数
		}

		// 4. 计算 a^(2^r * d) % p
		passed := false
		for r := int64(0); r < s; r++ {
			x = new(big.Int).Exp(x, big.NewInt(2), p) // x = x^2 % p
			if x.Cmp(big.NewInt(1)) == 0 {
				return false // 如果中途 x 变为 1，则 p 不是素数
			}
			if x.Cmp(new(big.Int).Sub(p, big.NewInt(1))) == 0 {
				passed = true
				break // x 成为 p-1，说明通过了该基数的检验
			}
		}

		if !passed {
			return false // 没有通过检验，p 不是素数
		}
	}
	return true
}

/*
3. 用于提供长度为n的数，用于提取大素数
*/
func GenerateBigRange(n int64) *big.Int {
	length := new(big.Int).SetInt64(n)
	re, _ := new(big.Int).SetString("10", 10) // 比如10的几次
	re.Exp(re, length, nil)
	return re
}

/*
4. 用于生成大素数
*/
func GenerateBigPrimeP(n int64) *big.Int {
	numRange := GenerateBigRange(n)
	ran := rand.New(rand.NewSource(time.Now().UnixNano())) //创建的时候需要初始化其中一个值 用于生成随机数
	ran.Seed(time.Now().UnixNano())

	p := new(big.Int).Rand(ran, numRange)
	for !MillerRabbin(p) {
		p.Rand(ran, numRange) //更新p
	}

	return p
}


/*
3. 用于提供长度为n的数，用于提取大素数
*/
func GenerateBigRange(n int64) *big.Int {
	length := new(big.Int).SetInt64(n)
	re, _ := new(big.Int).SetString("10", 10)
	re.Exp(re, length, nil)
	return re
}

/*
4. 用于生成大素数
*/
func GenerateBigPrimeP(n int64) *big.Int {
	numRange := GenerateBigRange(n)
	ran := rand.New(rand.NewSource(time.Now().UnixNano())) //创建的时候需要初始化其中一个值 用于生成随机数
	ran.Seed(time.Now().UnixNano())

	p := new(big.Int).Rand(ran, numRange)
	for !MillerRabbin(p) {
		p.Rand(ran, numRange) //更新p
	}

	return p
}

main.go代码

功能不必多说，就是调用生成

package main

import (
	"bufio"
	"fmt"
	"math/big"
	"os"
)

func main() {
	reader := bufio.NewReader(os.Stdin)
	println("请输入要加密的明文：")
	input, err := reader.ReadString('\n')
	if err != nil {
		panic("输入报错！")
	}
	input = input[:len(input)-1] // 去除换行符
	fmt.Println("明文为：", input)

	var p int64
	var q int64

	print("请输入要生成的p的位数: ")
	fmt.Scanf("%d", &p)
	fmt.Scanln() //吸收回车符

	print("请输入要生成的q的位数: ")
	fmt.Scanf("%d", &q)

	HugeP := GenerateBigPrimeP(p)
	HugeQ := GenerateBigPrimeP(q)
	fmt.Println("生成的p：", HugeP)
	fmt.Println("生成的q：", HugeQ)

	n := Calculate_n(HugeP, HugeQ)
	varphi := Calculate_varphi(HugeP, HugeQ)
	fmt.Println("计算varphi = (p-1)*(q-1)结果为:", varphi)

	e := big.NewInt(65537)
	fmt.Println("公钥是：", e)

	// 开始加密
	ciphertext, err := Encrypt(e, n, input)
	if err != nil {
		fmt.Println("加密失败:", err)
		return
	}

	// 输出密文
	fmt.Println("密文为：")
	for _, c := range ciphertext {
		fmt.Print(c, " ")
	}
	fmt.Println()

	// 开始解密
	fmt.Println("----------------------\n")
	fmt.Println("解密验证之\n")
	d, err := GetPrivate_d(e, varphi)
	if err != nil {
		fmt.Println(err)
	}

	// 解密
	decryptedMessage, err := Decrypt(d, n, ciphertext)
	if err != nil {
		fmt.Println("解密失败:", err)
		return
	}

	fmt.Println("\n解密后的明文是：", decryptedMessage, "\n")

}

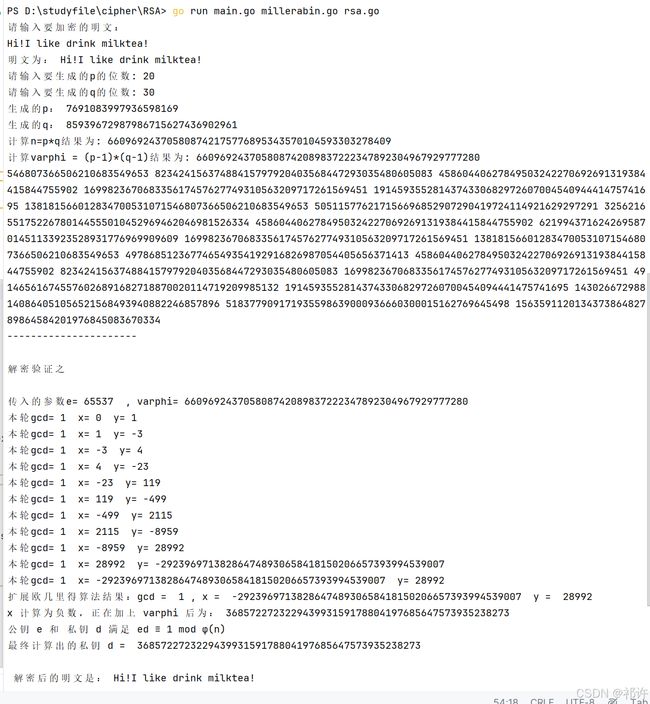
三 实现效果

可以实现字符串加解密，支持英文、汉字

效果图1



效果图2

---

参考文章 ：

1. go语言生成大素数
2. 米勒-拉宾素性检验(MillerRabbin)算法详解
3. RSA加密解密算法原理以及实现