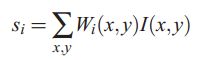一些知识点的初步理解_9(独立成分分析-ICA,ing...)
独立成分分析(后面都用ICA代替)在维基百科中的解释是:一种利用统计原理进行计算的方法它是一个线性变换。这个变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。独立成分分析是盲信号分离(Blind source separation)的一种特例。
可以感性上对比下ICA和PCA的区别,PCA是将原始数据降维并提取出不相关的属性,可以参考前面博文的介绍:PCA算法学习_1(OpenCV中PCA实现人脸降维)和PCA算法学习_2(PCA理论的matlab实现),而ICA是将原始数据降维并提取出相互独立的属性。我们知道两个随机变量独立则它们一定不相关,但2个随机变量不相关则不能保证它们不独立,因为独立是表示没有任何关系,而不相关只能表明是没有线性关系。且PCA目的是找到这样一组分量表示,使得重构误差最小,即最能代表原事物的特征。ICA的目的是找到这样一组分量表示,使得每个分量最大化独立,能够发现一些隐藏因素。由此可见,ICA的条件比PCA更强些。
另外,对任意两个相互独立的随机变量s1和s2,有下面的关系式成立:
其中的函数g1和g2是任意的非线性变换(当然也包括了线性变换),也就是说任意的相互独立的随机变量的任意非线性变换后是不相关的。
ICA的理解可以首先看下面的公式:
我们的目的就是要根据已知向量X(可以把矩阵转换成向量)来求出变换矩阵A和对应的系数列向量s。此时这里只已知了X。并且在求A和s的过程中有下面几个假设:
1. s中的每个元素是相互统计独立的。
2. s中的每个元素是非高斯分布的。
3. 变换矩阵A是可逆方阵。
4. s中元素的平方和为1.
至于具体怎么去求解A和s,都是一些数学优化的东西,没怎么看懂,这节就不介绍了(本节目标也只是初步理解下ICA)。
下面来看看ICA模型在图片分析中的理解:
一般情况下我们的图片都是基于像素表示的,即图片中的每个位置给出一个像素值,然后保存这些像素值即可。不过这里我们采用基于图片basis的表示方法,即对一张图片用少数几个系数和对应的一组basis images表示。Basis image指的是基图片,即其它的图片可以用这些basis image线性组合表示,有点类似基坐标系这一概念。如下图所示,一副图片可以用几个basis image表示:
其数学上的表示可以表示如下:
其中Ai就可以看做是basis image,Si可以看成是basis images图片的系数。当然了经过一系列的数学分析,Si是可以从原图像I(x,y)中求到的,公式如下:
参考文献:
A. Hyvarinen, J. Hurri, and P. Hoyer. Natural Image Statis-tics. Springer, 2009
独立成分分析Independent Component Analysis (ICA).ppt