基于麻雀优化算法的路径优化问题（Matlab代码实现）

    欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

1. 引言

2. 麻雀搜索算法（SSA）原理

3. 改进策略

4. 实验与结果展示

5. 考虑几何约束条件的路径优化

6. 结论与展望

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

      路径规划是移动机器人技术研究领域中非常重要的部分。面对愈渐复杂的工作环境，传统的路径规划技术存在各种难以解决的问题，如计算量大、完备性差、需要环境精确建模等，难以满足现代的实际需求。因此，无需环境精确建模、结构简单且通用性高的智能优化算法便成为路径规划研究的新兴热点。

麻雀搜索算法是2019年提出的群智能优化算法，其思想来源是麻雀种群的觅食行为和反捕食行为。麻雀搜索算法由于其结构简单、收敛速度快等优点，已经在一些实际工程问题上得到应用。因此，本研究基于麻雀搜索算法对移动机器人路径规划问题进行研究。

1. 引言

路径规划是智能车行驶控制领域的研究热点之一，其目标是在搜索空间内找到一条连接起点到终点的安全无碰撞且能量损耗低的车辆行驶路径。当前，大多数路径规划的研究成果都是通过调整和改进路径规划算法得到的。本文将麻雀搜索算法（Sparrow Search Algorithm，SSA）应用于求解路径优化问题，并对其进行了改进以解决应用过程中存在的问题。

2. 麻雀搜索算法（SSA）原理

麻雀搜索算法是一种新兴的群体智能优化算法，它基于自然界麻雀觅食行为的启发式优化策略，通过模拟麻雀在搜索食物时的行为来解决各种优化问题。在路径优化问题中，SSA可以用于寻找最优路径，使得路径的总长度最短或满足一定的约束条件。

3. 改进策略

针对SSA在路径优化问题中存在的收敛精度低和易陷入局部最优等问题，本文提出了以下改进策略：

• 引入混沌映射：为了提高算法的收敛能力和遍历性，引入混沌映射（如Adaptive-Tent混沌映射）来进行种群初始化，以增加初始种群中的多样性和随机性。
• 改进位置更新公式：优化麻雀位置更新公式，并优化种群冗余操作，以增强算法跳出局部最优的能力。
• 引入多策略增强：结合多种策略（如自适应正弦行走策略、轮盘赌选择学习策略、两阶段演化策略等）来增强SSA的性能，提高搜索的多样性和全局搜索能力。

4. 实验与结果展示

为了验证改进后的麻雀搜索算法在路径优化问题中的性能，本文进行了以下实验：

• 构建不同大小的地图：构建空间大小不同的两组环境，每组分别设置三个障碍物数量依次递增的地图。
• 应用改进算法求解：使用改进后的麻雀搜索算法在这些地图上求解路径规划问题。
• 结果对比：将改进后的算法与原始算法进行对比，分析最优路径长度、最优路径的拐点数目和收敛速度等指标。

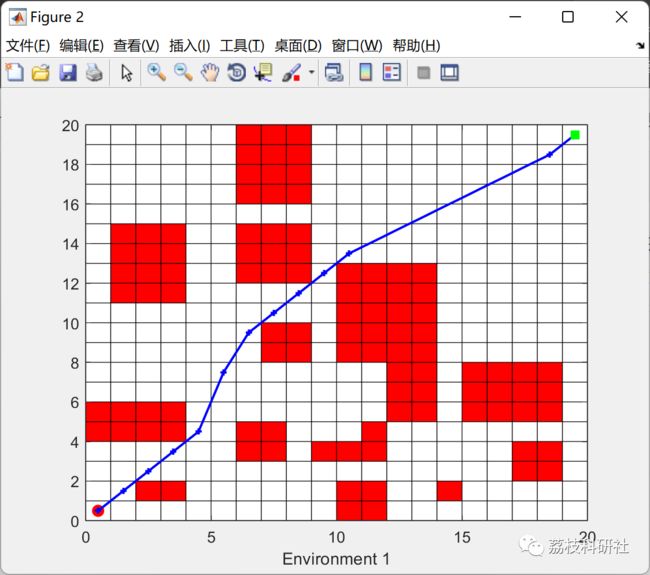
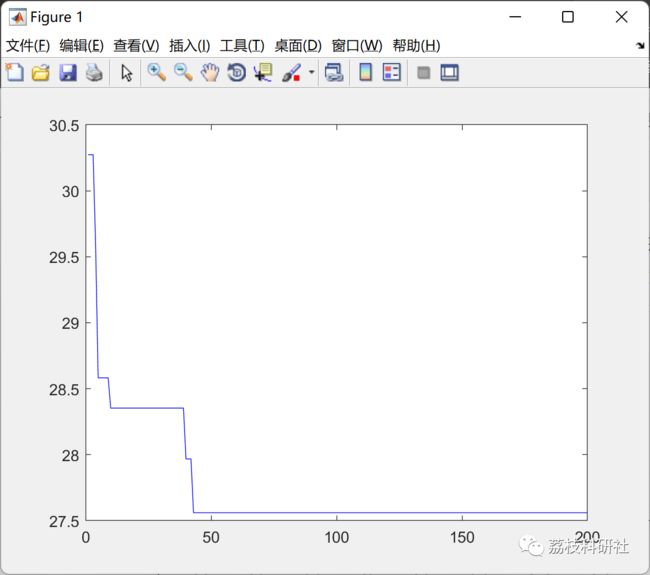
实验结果表明，在不同大小的地图中，改进后的麻雀搜索算法相较于原始算法在最优路径长度、拐点数目和收敛速度等方面均有所改善，说明在求解路径规划问题中有更好的表现。

5. 考虑几何约束条件的路径优化

在进一步考虑几何约束条件对路径规划造成的影响时，发现最优路径并不足以满足车辆几何尺寸和行驶特征的要求。为了解决这一问题，本文提出了一种融合优化算法的路径规划方法，使用贝塞尔曲线对路径进行优化，以确保最优路径可以满足车辆的几何约束条件，从而有效保证行驶安全。

6. 结论与展望

本文提出了一种基于改进麻雀搜索算法的智能车路径规划方法，并通过实验验证了其有效性。未来工作可以进一步探索如何结合其他优化算法和技术来提高路径规划的性能和鲁棒性。

2 运行结果

部分代码：

%% 参数设置
max_gen = 200;    % 最大迭代次数
num_polution = 50;         % 种群数量
soft_value = 0.8;        %安全值
recover_Percent = 0.3;  %%发现者比例
scout_Percent = 0.2;  %%侦查者比例
recover_Num = round( num_polution * recover_Percent );    % %发现者
scout_Num = round(num_polution * scout_Percent);      %%侦查者数量
X_min = 1;  

%% 初始化
X = zeros(num_polution,dimensions);
for i = 1:num_polution
    for j = 1:dimensions
       column = G(:,j+1);      % 地图的一列
       id = find(column == 0); % 该列自由栅格的位置
       X(i,j) =  id(randi(length(id))); % 随机选择一个自由栅格
       id = [];
    end 
    fit( i ) = fitness(X( i, : ),G);%%%行向量
end
fit_person_best = fit;   % 个体最优适应度
person_best = X;      % 个体最优位置
[fit_global_best, best_person_Index] = min( fit );        % 全局最优适应度
global_best = X(best_person_Index, : );    % 全局最优位置
[fit_max,B]=max(fit);
worse_person= X(B,:);  
%%
for gene = 1:max_gen
    gene
    [ans1,sort_Index] = sort(fit);   %适应值度从小到大排序
    [fit_max,B] = max(fit);
    worse_person = X(B,:);           %找出适应度最差的个体
    [~,Index] = sort(fit_person_best);
    r2 = rand(1);
    if r2 < soft_value

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

        for i = 1:recover_Num                                                  
            r1 = rand(1);  
            X(Index(i),:) = person_best(Index(i),:)*exp(-(i)/(r1*max_gen));         %%%%%发现者广泛进行搜索操作
            X(Index(i),:) = Bounds(X(Index(i),:), X_min,Xmax);                      %%%%输出整数路径
            fit(Index(i)) = fitness(X(Index(i),:),G);
        end
    else
            X(Index(i),:) = person_best(Index(i),:) + randn(1)*ones(1,dimensions);  %%%%%%%飞往其他地方觅食
            X(Index(i),:) = Bounds(X(Index(i),:),X_min,Xmax);    
            fit(Index(i)) = fitness(X(Index(i),:),G);
    end

3 参考文献

[1]张恩浩. 基于麻雀搜索算法的移动机器人路径规划算法研究[D].重庆理工大学,2022.DOI:10.27753/d.cnki.gcqgx.2022.000820.

‍4 Matlab代码