代码随想录算法训练营第三天 | 链表理论基础，203.移除链表元素，707.设计链表，206.反转链表

代码随想录算法训练营第三天 | 链表理论基础，203.移除链表元素，707.设计链表，206.反转链表

203.移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

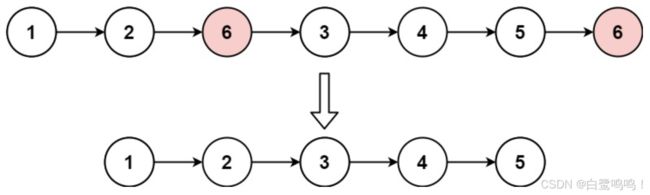
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

提示：

• 列表中的节点数目在范围 [0, 104] 内
• 1 <= Node.val <= 50
• 0 <= val <= 50

1.不使用虚拟头节点，在原链表中进行操作

思想：在删除目标节点时，由于链表是单向链表，只能通过寻找到目标节点的上一个节点，并改变上一个节点的指向（指向目标节点的下一个节点）来实现。对于头节点，由于没有前置节点，因此需要特殊考虑。并且在寻找的过程中应当注意要寻找的节点是否为空，为空的话需要停止寻找。

注意：头节点的指向不能改变，要定义一个临时节点，因为最后要靠头节点获取列表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //考虑目标节点是头节点的情况
        while(head != null && head.val == val){
            head = head.next;
        }
        //一般情况,头节点保持不动
        ListNode cur = head;
        while(cur != null && cur.next != null){
            if(cur.next.val == val){
                cur.next = cur.next.next;
            }else{
                cur = cur.next;
            }
        }
        return head;
    }
}

2.使用虚拟头节点

思想：定义一个虚拟头节点指向真实头节点，使得头节点不需要特殊考虑，减少代码量。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummyHead = new ListNode();
        dummyHead.next = head;
        ListNode cur = dummyHead;
        while(cur.next != null){
            if(cur.next.val == val){
                cur.next = cur.next.next;
            }else{
                cur = cur.next;
            }
        }
        return dummyHead.next;
    }
}

707.设计链表

你可以选择使用单链表或者双链表，设计并实现自己的链表。

单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。

如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。

实现 MyLinkedList 类：

• MyLinkedList() 初始化 MyLinkedList 对象。
• int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
• void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
• void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
• void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。
• void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

示例：

• 输入
  [“MyLinkedList”, “addAtHead”, “addAtTail”, “addAtIndex”, “get”, “deleteAtIndex”, “get”]
  [[], [1], [3], [1, 2], [1], [1], [1]]
  输出
  [null, null, null, null, 2, null, 3]
• 解释
  MyLinkedList myLinkedList = new MyLinkedList();
  myLinkedList.addAtHead(1);
  myLinkedList.addAtTail(3);
  myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3
  myLinkedList.get(1); // 返回 2
  myLinkedList.deleteAtIndex(1); // 现在，链表变为 1->3
  myLinkedList.get(1); // 返回 3

提示：

• 0 <= index, val <= 1000
• 请不要使用内置的 LinkedList 库。
• 调用 get、addAtHead、addAtTail、addAtIndex 和 deleteAtIndex 的次数不超过 2000 。

思考：这里使用了虚拟头节点，因此在考虑所有操作的时候注意都要考虑虚拟头节点（虚拟头节点的实现通过无参构造函数实现，每新建一个对象的时候，就默认生成一个值为0的虚拟头节点）。

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */
class ListNode{
    int val;
    ListNode next;
    public ListNode(int val){
        this.val = val;
    }
}
class MyLinkedList {
    ListNode head;
    int size;
    //这里的构造函数表明，只要新建一个对象的时候，就会默认生成一个节点（充当虚拟头节点）
    public MyLinkedList() {
        this.size = 0;
        this.head = new ListNode(0);
    }
    //有虚拟头节点，那么第一个节点的下标就是从1开始的,那么size就是记录的个数
    public int get(int index) {
        if(index < 0 || index >= size ){
            return -1;
        }
        //现在寻找的就是第index+1个节点,当index=0时，也就是要获取第一个节点，此时由于虚拟头节点的存在，需要往后移一位
        ListNode cur = this.head;
        while(index >= 0){
            cur = cur.next;
            index--;
        }
        return cur.val;
    }

    public void addAtHead(int val) {
        ListNode newNode = new ListNode(val);
        ListNode cur = this.head;
        newNode.next = cur.next;
        cur.next = newNode;
        size++;
    }

    public void addAtTail(int val) {
        ListNode newNode = new ListNode(val);
        ListNode cur = this.head;
        //也就是找到最后一个节点,此时一共有size个节点
        int index = size;
        while(index > 0){
            cur = cur.next;
            index--;
        }
        cur.next = newNode;
        size++;
    }

    public void addAtIndex(int index, int val) {
        if(index < 0 || index > size){
            return;
        }
        ListNode pre = this.head;
        //当index=0时，很明显已经找到前驱，不需要循环
        for(int i = 0;i < index;i++){
            pre = pre.next;
        }
        ListNode newNode = new ListNode(val);
        newNode.next = pre.next;
        pre.next = newNode;
        size++;
    }

    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        //找到前驱节点后，改变指向即可
        ListNode pre = this.head;
        //当index=0时,已经找到前驱，所以不需要循环
        for(int i = 0;i < index;i++){
            pre = pre.next;
        }
        pre.next = pre.next.next;
        size--;
    }
}

注意：在赋值的时候，要注意是改变本身的值还是自己指向的下一个值。

206.反转链表

1.双指针

思想：

• 在原链表操作，原链表中，原先是当前节点指向自己身后的节点，现在需要指向自己身前的节点。反转后，尾节点为头节点，原先的头节点为尾节点。为方便操作，需要定义cur指向当前节点，并定义pre之前身前的节点，方便操作，并且由于反转后，原先的头节点的下一个节点为null，所以可以给pre赋予初值null；
• 在操作时循环的终止条件为当前节点的指向为null。（可以考虑极端情况，当cur=cur-next=null时，null就不需要再指向pre了）

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        while(cur != null){
            ListNode node = cur;
            cur = cur.next;
            node.next = pre;
            pre = node;
        }
        return pre;
    }
}

2.递归

思想：参考双指针法的思想。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        return reverse(head,null);
    }

    public ListNode reverse(ListNode cur,ListNode pre){
        //终止条件
        if(cur == null){
            return pre;
        }
        ListNode temp = cur.next;
        cur.next = pre;
        //在改变cur以及pre的时候进行递归操作
        //cur = cur.next;
        //pre = cur;
        return reverse(temp,cur);
    }
}

注意：在递归过程中，应当用return返回递归函数的值，否则中间计算的值无法保存均会丢失。（通过阶乘理解）

示例：计算阶乘

假设我们要计算一个数的阶乘，使用递归的方法。

正确的实现

这里是一个正确实现的阶乘计算函数：

class Solution {
    public int factorial(int n) {
        return calculateFactorial(n); // 正确返回结果
    }

    private int calculateFactorial(int n) {
        if (n == 0) {
            return 1; // 基本情况
        }
        return n * calculateFactorial(n - 1); // 递归调用并返回结果
    }
}

执行流程

• 如果我们调用

  factorial(5)
  

  ，执行流程如下：

  1. calculateFactorial(5) 返回 5 * calculateFactorial(4)
  2. calculateFactorial(4) 返回 4 * calculateFactorial(3)
  3. calculateFactorial(3) 返回 3 * calculateFactorial(2)
  4. calculateFactorial(2) 返回 2 * calculateFactorial(1)
  5. calculateFactorial(1) 返回 1 * calculateFactorial(0)
  6. calculateFactorial(0) 返回 1

最终，factorial(5) 返回 120，结果正确。

错误的实现

现在，我们看一下如果在递归调用中不返回结果会发生什么：

class Solution {
    public int factorial(int n) {
        return calculateFactorial(n); // 正确返回结果
    }

    private int calculateFactorial(int n) {
        if (n == 0) {
            return 1; // 基本情况
        }
        calculateFactorial(n - 1); // 忽略返回值
        return n; // 这里只返回当前 n，没有计算完整的阶乘
    }
}

执行流程

• 如果我们调用

  factorial(5)
  

  ，执行流程如下：

  1. calculateFactorial(5) 调用 calculateFactorial(4)，但不处理返回值。
  2. calculateFactorial(4) 调用 calculateFactorial(3)，同样不处理返回值。
  3. 这个过程一直继续到 calculateFactorial(0)，返回 1。
  4. 然后返回到 calculateFactorial(1)，这时返回的是 1（未乘以任何值）。
  5. 最终，calculateFactorial(5) 返回 5，而不是 120。

最终结果

• 在错误的实现中，factorial(5) 返回 5，这是不正确的，因为没有将递归的返回值用于计算最终的阶乘结果。

总结

这个例子清楚地说明了：

• 如果在递归中不返回值，最终结果可能会是错误的。
• 计算的中间结果不会被有效利用，导致最终的输出不正确。

通过这个简单的阶乘例子，可以很容易地理解返回值在递归中的重要性。