数位dp模板简单解析
数位dp题目及其模板简单解析
题目
数字游戏II
题目描述
由于科协里最近真的很流行数字游戏。
某人又命名了一种取模数,这种数字必须满足各位数字之和 mod N 为 0。
现在大家又要玩游戏了,指定一个整数闭区间 [a.b],问这个区间内有多少个取模数。
输入格式
输入包含多组测试数据,每组数据占一行。
每组数据包含三个整数 a,b,N。
输出格式
对于每个测试数据输出一行结果,表示区间内各位数字和 mod N 为 0 的数的个数。
数据范围
1 ≤ \le ≤ a, b ≤ \le ≤ 2 31 2^{31} 231,
1 ≤ \le ≤ N < < < 100
输入样例
1 19 9
输出样例
2
解析
写在前面
数位dp中的概念介绍-----限定值
对于一个一共有5位的数 xxxxx,我们对其进行填写,假设最高位的限定值是6,则这个5位数的最高位只能填1—6中的一个数(假设不存在前导0)
即 这个5位数只能填 6xxxx、5xxxx、4xxxx、3xxxx、2xxxx、1xxxx说法
某个数(num)的某位的限定值是x
问题分析
设一个数,十进制表示为 a n − 1 a n − 2 a n − 3 . . . a 2 a 1 a 0 ⏟ n 位 \underbrace {a_{n-1}a_{n-2}a_{n-3}...a_{2}a_{1}a_{0}}_{n位} n位 an−1an−2an−3...a2a1a0
对于一个数,满足取模数的条件是 ( a n − 1 + a n − 2 + a n − 3 + . . . + a 2 + a 1 + a 0 ) (a_{n-1} + a_{n-2} + a_{n-3} + ... + a_{2} + a_{1} + a_{0}) (an−1+an−2+an−3+...+a2+a1+a0) % N == 0
分析填数,计算从0~ a n − 1 a n − 2 a n − 3 . . . a 2 a 1 a 0 a_{n-1}a_{n-2}a_{n-3}...a_{2}a_{1}a_{0} an−1an−2an−3...a2a1a0中满足取模数的个数
分析填数一般从高位开始填写,最先填写的位为 第n - 1位
则依题意 十进制表示为 a n − 1 a n − 2 a n − 3 . . . a 2 a 1 a 0 a_{n-1}a_{n-2}a_{n-3}...a_{2}a_{1}a_{0} an−1an−2an−3...a2a1a0 则第n-1位的限定值为 a n − 1 a_{n - 1} an−1
按如下的这种填法
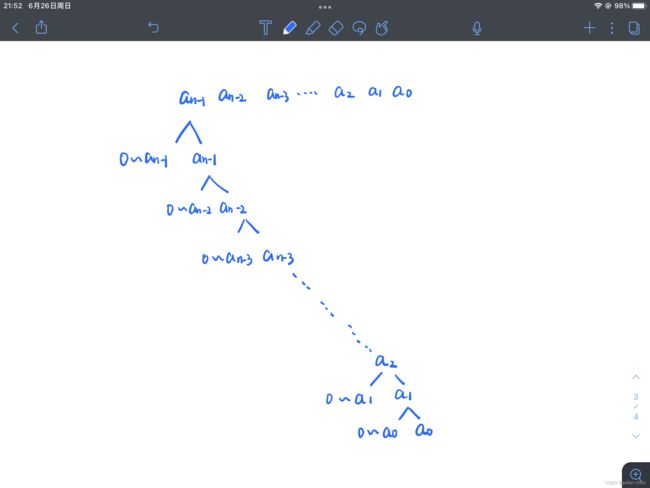
最高位的填法我们将其分为以下两种状况 填 a n − 1 a_{n - 1} an−1 、填0~ a n − 1 a_{n-1} an−1
1.填 0~ a n − 1 a_{n - 1} an−1 我们将用dp的方式进行计算,稍后会讲
2.填 a n − 1 a_{n - 1} an−1,表示该位已填完,我们填写下一位
次高位的填法我们也将其分为两种状况填 a n − 2 a_{n - 2} an−2 、填0~ a n − 2 a_{n-2} an−2
1.填 0~ a n − 2 a_{n - 2} an−2 我们将用dp的方式进行计算,稍后会讲
2.填 a n − 2 a_{n - 2} an−2,表示该位已填完,我们填写下一位
···
第2位的填法我们也将其分为两种状况填 a 2 a_{2} a2 、填0~ a 2 a_{2} a2
1.填 0~ a 2 a_{2} a2 我们将用dp的方式进行计算,稍后会讲
2.填 a 2 a_{2} a2,表示该位已填完,我们填写下一位
第1位的填法我们也将其分为两种状况填 a 1 a_{1} a1 、填0~ a 1 a_{1} a1
1.填 0~ a 1 a_{1} a1 我们将用dp的方式进行计算,稍后会讲
2.填 a 1 a_{1} a1,表示该位已填完,我们填写下一位
第0位的填法我们也将其分为两种状况填 a 0 a_{0} a0 、填0~ a 0 a_{0} a0
1.填 0~ a 0 a_{0} a0 我们将用dp的方式进行计算,稍后会讲
2.填 a 0 a_{0} a0,表示该位已填完,我们填写下一位
如此满足从 0~ a n − 1 a n − 2 a n − 3 . . . a 2 a 1 a 0 a_{n-1}a_{n-2}a_{n-3}...a_{2}a_{1}a_{0} an−1an−2an−3...a2a1a0 取模数的所有个数可以表示为:每位填法中的填第一种状况的方案数(每位中填0 ~ a n − i a_{n - i} an−i的方案数 )之和 + { 特判 ( a n − 1 + a n − 2 + a n − 3 + . . . + a 2 + a 1 + a 0 ) (a_{n-1} + a_{n-2} + a_{n-3} + ... + a_{2} + a_{1} + a_{0}) (an−1+an−2+an−3+...+a2+a1+a0) % N == 0, 为 true 则为1,否则为0}
计数计算
现在介绍 每位填法中的填第一种状况的方案数的算法,这个是数位dp的难点
对于数 a n − 1 a n − 2 a n − 3 . . . a 2 a 1 a 0 a_{n-1}a_{n-2}a_{n-3}...a_{2}a_{1}a_{0} an−1an−2an−3...a2a1a0 假设我们填写第k位 即 a n − 1 a n − 2 a n − 3 . . . a k . . . a 2 a 1 a 0 a_{n-1}a_{n-2}a_{n-3}...a_{k}...a_{2}a_{1}a_{0} an−1an−2an−3...ak...a2a1a0
我们需要计算 填0~ a k a_{k} ak 这种情况中的方案数
即我们填写限定数是 a k − 1 a_{k} - 1 ak−1 中的方案
我们依次在该位枚举0~ a k − 1 a_{k} - 1 ak−1 计算其方案数即可
我们采用动态规划的思想
则该计算转化为动态规划的计算
采用闫氏dp分析法
状态表示 f[i][j][k] :表示枚举到第i位,且第i位数是j,且 所有位数之和 %N 的余数是k的方案数
/
状态表示
\
属性:nums(方案数)
/
dp
\
状态计算
根据状态表示,第i位已经填好,因此只考虑第i - 1位 设第i - 1位填x, 所有位数之和的余数是k
则有 { (前i - 1位的和) + j + (剩下的位数之和) } % N = k
我们解得 { (前i - 1位的和) + (剩下的位数之和) } % N = (k - j) % N
于是只要余数为 (k - j) % N,则表示可以进行状态转移
于是我们得到状态转移方程
f[i][j][k] += f[i - 1][x][(k - j) % N]
参考代码
import java.util.Scanner;
import java.util.ArrayList;
import java.util.Arrays;
class Main{
static int N = 11, M = 110;
static int p, l, r;
static int f[][][] = new int[N][10][M];
static int mod(int x, int y){
return (x % y + y) % y;
}
static void init(){
for (int i = 0 ; i < N; i ++)
for (int j = 0; j <= 9; j ++)
Arrays.fill(f[i][j], 0);
for (int i = 0; i <= 9; i ++) f[1][i][mod(i, p)] ++;
for (int i = 2; i < N; i ++)
for (int j = 0; j <= 9; j ++)
for (int k = 0; k < p; k ++)
for (int x = 0; x <= 9; x ++)
f[i][j][k] += f[i - 1][x][mod(k - j, p)];
}
static int dp(int n){
if (n == 0) return 1;
ArrayList nums = new ArrayList<>();
while (n > 0){
nums.add(n % 10);
n /= 10;
}
int res = 0, last = 0;
for (int i = nums.size() - 1; i >= 0; i -- ){
int x = nums.get(i);
for (int j = 0; j < x; j ++)
res += f[i + 1][j][mod(-last, p)];
last += x;
if (i == 0 && last % p == 0) res ++;
}
return res;
}
public static void main(String[]args){
Scanner sc = new Scanner(System.in);
while (sc.hasNext())
{
l = sc.nextInt(); r = sc.nextInt(); p = sc.nextInt();
init();
System.out.println(dp(r) - dp(l - 1));
}
sc.close();
}
}