七大排序算法详解:从原理到实现(希尔/堆排/快排/冒泡等)
目录
引言
1. 希尔排序(Shell Sort)
2. 堆排序(Heap Sort)
3. 快速排序(Quick Sort)
(1)PartSort1(快排原型)
(2)PartSort2(挖坑法)
(3)PartSort3(前后指针法)
4. 快速排序(Quick-random Sort)
(1).随机取key
(2)三数取中
5.非递归快速排序(Non-Recursive Quick Sort)
6.三路划分快速排序(3-Way Quick Sort)
7. 冒泡排序(Bubble Sort)
8. 插入排序(Insertion Sort)
9. 归并排序(Merge Sort)
10.非递归归并排序(Non-Recursive Merge Sort)
11. 选择排序(Selection Sort)
引言
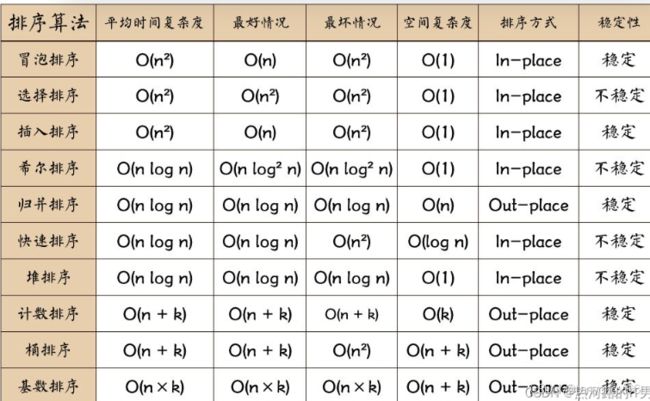
排序算法是计算机科学的基石之一。本文将系统讲解7种经典排序算法,通过:
✅ 分步图解算法流程
✅ 语言代码实现
✅ 实测性能对比
帮助你彻底掌握排序算法的核心原理与应用场景。
1. 希尔排序(Shell Sort)
原理:
插入排序的改进版,通过将数组按增量序列分组(如间隔 gap = length/2),对每组进行插入排序,逐步缩小增量直至为1,最终进行一次全数组插入排序。
关键点:
-
增量序列的选择影响效率(常用
gap = gap/3 + 1)。 -
时间复杂度:平均O(n log n) ~ O(n²)。
代码:
void ShellSort(int* a, int n)//希尔排序
{
int gap = 10;
while (gap > 1)
{
gap /= 2;
for (int j = 0;j < gap;j++)
{
for (int i = j;i < n - gap;i = i + gap)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp 2. 堆排序(Heap Sort)
原理:
-
建堆:将数组视为完全二叉树,调整成最大堆(父节点值 ≥ 子节点)。
-
排序:交换堆顶元素(最大值)与末尾元素,缩小堆范围并重新调整堆,重复直至有序。
关键点: -
时间复杂度:O(n log n),且是原地排序。
-
不稳定排序。
实现该代码需要我们把堆建立起来
堆代码:
//这是stack.h的代码
#pragma once
#include
#include
#include
#include
typedef int STDataType;
typedef struct Stack
{
STDataType * a;
int capacity;
int top;
}ST;
void STInit(ST*ps);
void STPush(ST* ps,STDataType x);
void STPop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
void STDestroy(ST* ps);
STDataType STTop(ST* ps);
//这是stack.c的代码
#include"stack.h"
void STInit(ST* ps)
{
assert(ps);
ps->a = malloc(sizeof(STDataType) * 4);
if (ps->a == NULL)
{
perror("malloc fail");
return;
}
ps-> capacity = 4;
ps->top = 0;
}
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);//新建一个变量加进去,需要我进行空间创建,然后扩容
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ps->a = tmp;
ps->capacity *= 2;
}
ps->a[ps->top] = x;
ps->top++;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
void STPop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));//等于空就报错
ps->top--;
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));//空的话咱们就不能取值了
return ps->a[ps->top - 1];//是空的话就越界了,哥们
}//访问栈顶元素 堆排序代码:
void HeapSort(int* a, int n)//栈排序
{
for (int i = (n - 1 - 1) / 2;i >= 0;--i)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
}3. 快速排序(Quick Sort)
原理:
-
分治策略:选基准值(pivot),将数组分为“小于pivot”和“大于pivot”两部分。
-
递归排序:对左右子数组递归执行快排。
关键点: -
时间复杂度:平均O(n log n),最坏O(n²)(可通过随机选pivot优化)。
-
不稳定排序。
代码:
(1)PartSort1(快排原型)
int PartSort1(int* a, int left, int right)//快速排序
{
int begin = left, end = right;
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//注意是>=不是<=
--right;
while (left < right && a[left] <= a[keyi])//注意是<=不是>=
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
return keyi;
}(2)PartSort2(挖坑法)
//挖坑法
int PartSort2(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right)
{
while (left < right && a[right] >= key)//注意是>=不是<=
--right;
a[hole] = a[right];
//hole = left;
hole = right;
while (left < right && a[left] <= key)
++left;
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}(3)PartSort3(前后指针法)
//前后指针法
int PartSort3(int* a, int left, int right)//快速排序
{
//int key = a[left]; 这样写是有错误的,与全局变量有关
int prev = left;
int cur = left + 1;
int keyi=left;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)//++prev!=cur 这是防止自我交换
Swap(&a[prev], &a[cur]);
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}4. 快速排序(Quick-random Sort)
原理:分治策略:随机选择基准值(pivot),将数组分为“小于pivot”和“大于pivot”两部分。
递归排序:对左右子数组递归执行快排。
关键点:
- 时间复杂度:平均 O(n log n),最坏 O(n²)(但通过随机选pivot可避免最坏情况,实际效率接近平均复杂度)。
- 不稳定排序(元素相对位置可能改变)。
- 核心优化:随机选择pivot能大幅降低最坏情况出现概率(如有序数组排序时,避免固定选首元素导致的性能退化)。
优化的代码:用PartSort1举例
(1).随机取key
//随机选key
int randi = (rand() % (right - left)) + left;
Swap(&a[left], &a[left]);优化后
int PartSort1(int* a, int left, int right)//快速排序
{
int begin = left, end = right;
//随机选key
int randi = (rand() % (right - left)) + left;
Swap(&a[left], &a[left]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//注意是>=不是<=
--right;
while (left < right && a[left] <= a[keyi])//注意是<=不是>=
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
return keyi;
}(2)三数取中
int GetMidNumi(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return right;
}
else
{
return left;
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
}优化后
int PartSort1(int* a, int left, int right)//快速排序
{
int begin = left, end = right;
//三数取中
int midi = GetMidNumi(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right)
{
while (left < right && a[right] >= a[keyi])//注意是>=不是<=
--right;
while (left < right && a[left] <= a[keyi])//注意是<=不是>=
++left;
Swap(&a[right], &a[left]);
}
Swap(&a[keyi], &a[left]);
keyi = left;
return keyi;
}5.非递归快速排序(Non-Recursive Quick Sort)
原理
- 栈模拟递归:用栈(或队列)存储待排序子数组的起止索引,替代递归调用栈。
- 分割操作:每次从栈中取出一个区间,用基准值(如首元素)分割为左右两部分。
- 循环处理:将分割后的左右子区间重新入栈,直到栈为空。
关键点
- 时间复杂度:平均 O(n log n),最坏 O(n²)(与递归版本一致)。
- 不稳定排序(分割可能改变相等元素的顺序)。
- 空间复杂度:最坏 O(n)(栈深度),平均 O(log n)。
- 原地排序(无需额外内存,仅需栈空间)。
堆代码:
//这是stack.h的代码
#pragma once
#include
#include
#include
#include
typedef int STDataType;
typedef struct Stack
{
STDataType * a;
int capacity;
int top;
}ST;
void STInit(ST*ps);
void STPush(ST* ps,STDataType x);
void STPop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
void STDestroy(ST* ps);
STDataType STTop(ST* ps);
//这是stack.c的代码
#include"stack.h"
void STInit(ST* ps)
{
assert(ps);
ps->a = malloc(sizeof(STDataType) * 4);
if (ps->a == NULL)
{
perror("malloc fail");
return;
}
ps-> capacity = 4;
ps->top = 0;
}
void STPush(ST* ps, STDataType x)
{
assert(ps);
if (ps->top == ps->capacity)
{
STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * ps->capacity * 2);//新建一个变量加进去,需要我进行空间创建,然后扩容
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ps->a = tmp;
ps->capacity *= 2;
}
ps->a[ps->top] = x;
ps->top++;
}
void STDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
void STPop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));//等于空就报错
ps->top--;
}
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
STDataType STTop(ST* ps)
{
assert(ps);
assert(!STEmpty(ps));//空的话咱们就不能取值了
return ps->a[ps->top - 1];//是空的话就越界了,哥们
}//访问栈顶元素 非递归快速排序代码:
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
//STDestroy(&st);这里就是有问题,搞不懂为什么要放在zui'hou'mian
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
int keyi = PartSort3(a, begin, end);
if (end - (keyi + 1) > 0)
{
STPush(&st, end);
STPush(&st, keyi+1);
}
if ((keyi - 1) - begin > 0)
{
STPush(&st, keyi-1);
STPush(&st, begin);
}
}
}6.三路划分快速排序(3-Way Quick Sort)
原理
- 重复元素优化:将数组划分为三部分:
< 基准值、= 基准值、> 基准值,减少对重复元素的重复比较。 - 三指针操作:使用
lt(less than)、i(当前遍历指针)、gt(greater than)动态分割区间。 - 跳过重复值:将等于基准值的元素集中在中间,仅对左右两侧递归排序。
关键点
- 时间复杂度:
- 平均 O(n log n),最坏 O(n²)(与常规快排一致)。
- 对重复元素多的数组效率显著提升(避免重复分割中间段)。
- 不稳定排序(元素交换可能破坏原始顺序)。
- 空间复杂度:最坏 O(n)(递归栈),平均 O(log n)。
- 原地排序(无需额外内存)。
//三路划分
void ThreeRoad(int* a, int left, int right)//快速排序
{
if (left >= right)
{
return 0;
}
随机选key
int randi = (rand() % (right - left)) + left;
Swap(&a[left], &a[left]);
int begin=left, end=right;
//int key = a[left]; 这样写是有错误的,与全局变量有关
int key = a[begin];
int cur = begin + 1;
while (cur<=right)
{
if (a[cur] < key)//++prev!=cur 这是防止自我交换
{
Swap(&a[left], &a[cur]);
++left;
cur++;
}
else if (a[cur] > key )//++prev!=cur 这是防止自我交换
{
Swap(&a[right], &a[cur]);
--right;
}
else
{
cur++;
}
}
ThreeRoad(a, begin, left - 1);
ThreeRoad(a, right + 1, end);
return 0;
}7. 冒泡排序(Bubble Sort)
原理:
重复遍历数组,比较相邻元素,若顺序错误则交换,每轮遍历将最大值“冒泡”到末尾。
关键点:
-
可优化:若某轮无交换,提前终止。
-
时间复杂度:最好O(n)(已有序),平均O(n²)。
代码:
void BubbleSort(int* a, int n)//冒泡排序
{
for (int j = 0;j < n;j++)
{
for (int i = 0;i < n-j-1;i++)
{
if (a[i ]> a[i+1])
{
Swap(&a[i + 1], &a[i]);
}
}
}
}8. 插入排序(Insertion Sort)
原理:
将数组分为 已排序 和 未排序 两部分,每次从未排序部分取出第一个元素,在已排序部分从后向前扫描,找到合适的位置插入。类似整理扑克牌的过程。
关键点:
-
原地排序(无需额外空间)。
-
时间复杂度:最好O(n)(已有序),平均O(n²)。
代码:
void InsertSort(int* a, int n)//插入排序
{
for (int i = 1;i < n;i++)
{
int end=i-1;
int tmp=a[i];
//将tmp插入[0,end]区间中,保持有序
while (end >= 0)
{
if (tmp 9. 归并排序(Merge Sort)
原理:
分治策略:将数组递归分解为两半,直到子数组长度为1(天然有序)。
合并阶段:将两个有序子数组按大小顺序合并为一个有序数组。
- 时间复杂度:始终为 O(n log n)(无论数据初始状态,稳定高效)。
- 稳定排序(合并时保留相等元素的原始顺序)。
- 空间复杂度:O(n)(需额外空间存储合并后的数组)。
- 非原地排序(依赖额外内存空间,适用于外部排序场景)。
代码:
void _MergeSort(int* a, int begin,int end,int * tmp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
//子区间递归排序 [begin,mid][mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//[begin,mid] [mid+1,end]归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;//这里不是
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));//这里是闭区间,所以是end-begin+1,开区间是end-begin
}
void MergeSort(int* a, int n)//归并排序//这个可以既称内排序又称外排序(外排序就是再磁盘中排序)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc is fail!");
return;
}
_MergeSort(a, 0,n-1,tmp);//前面加一个杠一般是程序的局部
free(tmp);
}10.非递归归并排序(Non-Recursive Merge Sort)
原理
- 自底向上合并:从单个元素开始,逐步合并相邻有序子数组。
- 步长倍增:按步长 1, 2, 4, 8... 合并,直到覆盖整个数组。
- 显式控制循环:无需递归分解,直接通过循环控制合并范围。
关键点
- 时间复杂度:稳定 O(n log n)(与递归版本一致)。
- 稳定排序(合并时保留相等元素顺序)。
- 空间复杂度:O(n)(需额外临时数组)。
- 非原地排序(依赖临时内存空间)。
代码:
void MergeSortNonR(int* a, int n) {
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//_MergeSort(a, 0, n - 1, tmp);
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2*gap - 1;
int j = begin1;
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if(begin2 >= n){
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n) {
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[j++] = a[begin1++];
else
tmp[j++] = a[begin2++];
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
memcpy(a, tmp, n * sizeof(int));
gap *= 2;
}
free(tmp);
}11. 选择排序(Selection Sort)
原理:
每次从未排序部分找到最小值,与未排序部分的第一个元素交换,逐步将最小值“选择”到左侧。
关键点:
-
不稳定排序(可能破坏相同元素顺序)。
-
时间复杂度:固定O(n²)。
代码:
void SelectSort(int* a, int n)//选择排序
{
int left = 0;
int right = n - 1;
while (left < right)
{
int mini = left, maxi = right;
for (int i = left; i <= right;i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
if (maxi == left)
{
maxi = mini;
}
Swap(&a[left], &a[mini]);
Swap(&a[right], &a[maxi]);
++left;
--right;
}
}