LeetCode热题100JS（37/100）第七天|排序链表|合并K个升序链表|LRU缓存|二叉树的中序遍历|二叉树的最大深度|对称二叉树

 148. 排序链表

题目链接：​​​​​​​148. 排序链表

难度：中等

刷题状态：1刷

新知识：

- `dic.reduceRight((t,c)=>(c.next=t,c),null)`  方法从数组的末尾开始执行

解题过程

思考

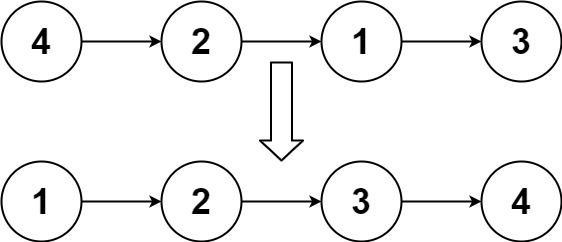
示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

当然可以转成数组排序再生成链表，但我感觉这考点应该不是这个

题解分析

参考题解链接：240. 搜索二维矩阵 II（贪心，清晰图解）

好吧，可以这么写，，而且速度还挺快

详细分析如下

var sortList = function(head) {
    let dic=[]
    while(head){
        //将当前节点压入数组中
        dic.push(head)
        head=head.next
    }    
    dic.sort((a,b)=>a.val-b.val)
//reduceRight 方法从数组的末尾开始执行，逐步向数组的开头移动。
//reduceRight 的回调函数接受两个参数：累加器 t 和当前值 c。

//t（累加器）：在每次迭代中，t 代表已经连接好的链表部分。在第一次迭代时，t 是 null，因为链表的最后一个节点的 next 应该是 null。

//(c.next = t, c) 是一个使用逗号运算符的表达式。
//c.next = t：将当前节点 c 的 next 指针指向累加器 t。这样就将当前节点连接到了已经连接好的链表部分。
//c：逗号运算符会返回其第二个操作数的结果，因此这里返回的是当前节点 c。这个返回值将成为下一次迭代中的累加器 t。
    return dic.reduceRight((t,c)=>(c.next=t,c),null)
}

手搓答案（无非废话版）

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
  
var sortList = function(head) {
    let dic=[]
    while(head){
        dic.push(head)
        head=head.next
    }
    dic.sort((a,b)=>a.val-b.val)
    return dic.reduceRight((t,c)=>(c.next=t,c),null)
}

总结

 done

  ​​​​​​​23. 合并 K 个升序链表

题目链接：​​​​​​​23. 合并 K 个升序链表

难度：困难

刷题状态：1刷

新知识：

- `lists.flat()`

- `const flatArray = nestedArray.reduce((accumulator, currentValue) => {
    return accumulator.concat(currentValue);
}, []);` 拍平数组

解题过程

思考

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

注意这里是链表数组

还是转换成数组处理好了再生成链表

题解分析

参考题解链接：​​​​​​​合并K个排序链表

手搓答案（无非废话版）

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    let dic=[]
    for(let l of lists){
        while(l){
            dic.push(l.val)
            l=l.next
        }
    }
    dic.sort((a,b)=>a-b)
    
    let dum=new ListNode(dic[0]),cur=dum
    if(!dic.length) return dum.next
    for(let i=1;i

总结

done

  ​​​​​​​146. LRU 缓存

题目链接：​​​​​​​146. LRU 缓存

难度：中等

刷题状态：1刷

新知识：

- `this.cache.keys().next().value;`  这行代码用于获取 Map 对象中最旧的键（即第一个插入的键）

解题过程

思考

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

一看就没刷过，直接看答案

题解分析

参考题解链接：240. 搜索二维矩阵 II（贪心，清晰图解）

详细分析如下

/**
 * @param {number} capacity
 */
 //LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
var LRUCache = function(capacity) {
    this.capacity = capacity; // 初始化缓存的最大容量
    this.cache = new Map();   // 使用 Map 对象来存储缓存的键值对
};


/** 
 * @param {number} key
 * @return {number}
 */
 //int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
LRUCache.prototype.get = function(key) {
    if (!this.cache.has(key)) {
        return -1; // 如果缓存中没有这个key，返回-1
    }
    // 获取值，并将该键值对移到 Map 的末尾，表示最近使用
    const value = this.cache.get(key);
    this.cache.delete(key);
    this.cache.set(key, value);
    return value;
};

/** 
 * @param {number} key 
 * @param {number} value
 * @return {void}
 */
 //void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。
LRUCache.prototype.put = function(key, value) {
    if (this.cache.has(key)) {
        // 如果键已经存在，删除旧记录
        this.cache.delete(key);
    } else if (this.cache.size >= this.capacity) {
        // 如果缓存已满，删除最旧的记录
        //this.cache 是一个 Map 对象。
        // keys() 方法返回一个迭代器对象，该迭代器对象按插入顺序包含 Map 对象中所有的键。
        // .next():
        // next() 方法被调用在迭代器对象上，用于获取迭代器中的下一个值。
        // next() 返回一个对象，该对象具有两个属性：value 和 done。
        // value 是当前迭代的值（在这个情况下是一个键）。
        const oldestKey = this.cache.keys().next().value;
        this.cache.delete(oldestKey);
    }
        // 插入新记录
    this.cache.set(key, value);
};

/** 
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */

手搓答案（无非废话版）

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */

var searchMatrix = function(matrix, target) {
    let tag=matrix[0].length-1
    for(let i=0;itarget) return false
        if(matrix[i][matrix[i].length-1]=0;j--){
            if(matrix[i][j]==target) return true
            if(matrix[i][j]>target){
                tag--
            }else{
                break
            }
        }
    }
    return false
}

总结

 难死了，不好理解，多看几遍

  ​​​​​​​94. 二叉树的中序遍历

题目链接：​​​​​​​​​​​​​​94. 二叉树的中序遍历

难度：简单

刷题状态：1刷

新知识：

解题过程

思考

示例 1：

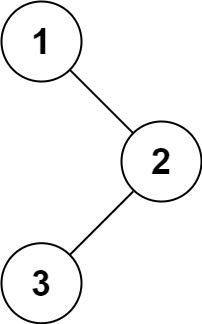
输入：root = [1,null,2,3]
输出：[1,3,2]

二叉树经典问题，就是我忘了

题解分析

参考题解链接：​​​​​​​二叉树的中序遍历

详细分析如下

var inorderTraversal = function(root) {
    let res=[]
    //箭头函数
    function inorder(root){
        if(!root) return 
        //体现了中序遍历的“先遍历左子树”的原则。
        inorder(root.left)
        //体现了中序遍历的“访问根节点”的步骤。
        res.push(root.val)
        //体现了中序遍历的“再遍历右子树”的原则。
        inorder(root.right)
    }
    inorder(root)
    return res
};

手搓答案（无非废话版）

/**
 * @param {TreeNode} root
 * @return {TreeNode} 
 */
 var inorderTraversal = function(root) {
    let res=[]
    function inorder(root){
        if(!root) return
        inorder(root.left)
        res.push(root.val)
        inorder(root.right)
    }
    inorder(root)
    return res
}

总结

 拿下

  ​​​​​​​104. 二叉树的最大深度

题目链接：​​​​​​​​​​​​​​​​​​​​​104. 二叉树的最大深度

难度：简单

刷题状态：2刷

新知识：

解题过程

思考

示例 1：

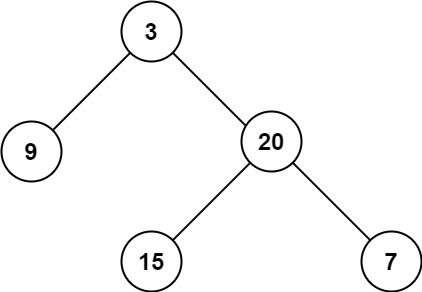
输入：root = [3,9,20,null,null,15,7]
输出：3

也是2刷了，放下1刷过程在题解

题解分析

参考题解链接：​​​​​​​画解算法：104. 二叉树的最大深度

详细分析如下

/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if(root){
        // console.log('root.left',root.left)
        // console.log('root.right',root.right)
        let left=maxDepth(root.left)
        let right=maxDepth(root.right)
        return Math.max(left,right) +1
    }else{
        return 0
    }
};

手搓答案（无非废话版）

/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    let res=0,i=0
    function depth(root){
        if(!root){
            res=Math.max(res,i)
            return 
        }
        i++
        let tmp=i
        depth(root.left)
        i=tmp
        depth(root.right)
    }
    depth(root)
    return res
};

总结

 emm,我用的是套路

  ​​​​​​​101. 对称二叉树

题目链接：​​​​​​​​​​​​​​​​​​​​​​​​​​​​101. 对称二叉树

难度：简单

刷题状态：2刷

新知识：

解题过程

思考

示例 1：

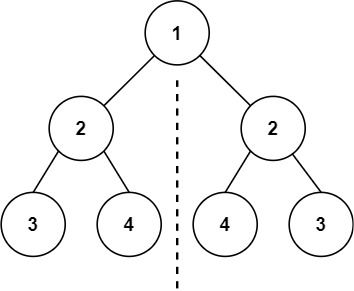
输入：root = [1,2,2,3,4,4,3]
输出：true

也是2刷了，放下1刷过程在题解

没写出来555

题解分析

参考题解链接：​​​​​​​对称二叉树

详细分析如下

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
function check(L,R){
        if(!L&&!R) return true
        if(!L||!R) return false
        let ret=L.val==R.val
        return ret&&check(L.left,R.right)&&check(L.right,R.left)
    }
var isSymmetric = function(root) {
    let res=check(root.left,root.right)
    return !root||res
};

手搓答案（无非废话版）

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */

var isSymmetric = function(root) {
    function check(l,r){
        if(!l&&!r) return true
        if(!l||!r) return false
        return l.val==r.val&&check(l.left,r.right)&&check(l.right,r.left)
    }
    return root?check(root.left,root.right):true
};

总结

 emm,我用的是套路