AtCoder Beginner Contest 275 A-D题解

比赛名称：AtCoder Beginner Contest 275

A - Find Takahashi

找出最大的元素并输出下标
使用两个变量一个存储当前找到的最大值一个存储找到的最大值对应的下标，若当前数大于最大值更新最大值和下标

AC代码

// Problem: A - Find Takahashi
// Contest: AtCoder - AtCoder Beginner Contest 275
// URL: https://atcoder.jp/contests/abc275/tasks/abc275_a
// Memory Limit: 1024 MB
// Time Limit: 2000 ms

#include 
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
const int N = 2e5 + 10;
const int MOD = 1e9 + 7;
#define endl '\n'
#define PY puts("Yes")
#define PN puts("No")
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    int ans = 0, max = 0;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        int x;
        cin >> x;
        if (x > max)
        {
            max = x;
            ans = i + 1;
        }
    }
    cout << ans;
    return 0;
}

---

B - ABC-DEF

（同余定理的应用）
$(a+b)\mathrm{mod}c=((a\mathrm{mod}c)+(b\mathrm{mod}c))\mathrm{mod}c$
$(a\times b)\mathrm{mod}c=((a\mathrm{mod}c)\times (b\mathrm{mod}c))\mathrm{mod}c$
但是我用Cpp写的代码始终过不去不懂为什么
于是选择python，直接暴力运算就好

AC代码

a,b,c,d,e,f = map(int,input().split())
ans = (a*b*c-d*e*f)%998244353
print(ans)

---

C - Counting Squares

题意

给出一个$9\times 9$的平面，上面有若干个点，判断它们能组成多少个正方形

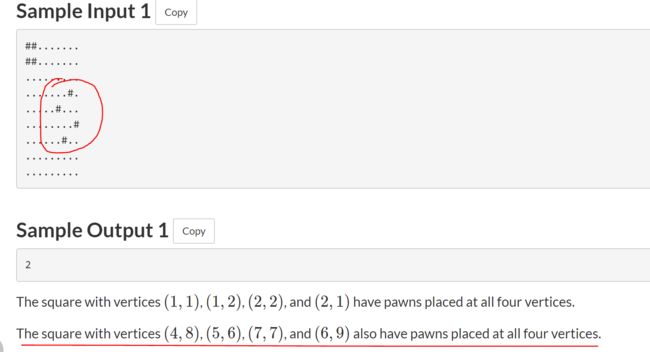
读题时候看到square还不太确定指的是正方形还是平行四边形，因为下面给出的样例打印出来的结果有一定误导性（笑哭），下图中圈出来的四个点其实组成了一个正方形，当时我看到这个还以为要求的平行四边形，导致写出了一个判断是否能组成平行四边形的函数，后面改成判断正方形的函数又花了不少时间

思路

这个题情况比较特殊，正方形的顶点可以不在同一行或者同一列，因此直接枚举每个点然后枚举边长来构造正方形很麻烦
这样子直接记录点的坐标，然后判断这些点组成正方形的可行性
由于棋盘大小为$9\times 9$的，最多有$81$个点，所以直接考虑暴力枚举四个顶点，最多$O(81^4)$的时间复杂度还是可以接受的，于是就有了平常很少看到的四重循环
使用四重循环枚举出所有的点组成四边形的情况后，对这些四边形（四个顶点）进行判断，如果是，答案加一
那么如何判断四个点可以组成正方形
暴力枚举四个点中的两个点，计算它们两两点之间的长度，将它们存起来然后排序，这样子会得到 $6$ 条边的长度，如果是正方形，其中排序后前 $4$ 条是它们边的长度，它们是相等的，后 $2$ 条是对角线的长度，他们也是相等的，排序后检查是否满足
下面的代码除了判断正方形的函数$issquare$外，还有一个$print$函数可以输出正方形四个顶点坐标，可以供调试使用

AC代码

// Problem: C - Counting Squares
// Contest: AtCoder - AtCoder Beginner Contest 275
// URL: https://atcoder.jp/contests/abc275/tasks/abc275_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms

#include 
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
const int N = 2e5 + 10;
const int MOD = 1e9 + 7;
#define endl '\n'
#define PY puts("Yes")
#define PN puts("No")
vector<pi> cord;
int len(pi a, pi b)
{
    return (a.first - b.first) * (a.first - b.first) + (a.second - b.second) * (a.second - b.second);
}
bool issquare(vector<pi> tojudge)
{
    vector<int> edgelen;
    for (int i = 0; i < 4; i++)
    {
        for (int j = i + 1; j < 4; j++)
        {
            edgelen.push_back(len(tojudge[i], tojudge[j]));
        }
    }
    sort(edgelen.begin(), edgelen.end());
    for (int i = 1; i < 4; i++)
        if (edgelen[i] != edgelen[0])
            return false;
    if (edgelen[4] != edgelen[5])
        return false;
    return true;
}
void print(vector<pi> tojudge)
{
    for (int i = 0; i < 4; i++)
    {
        cout << "( " << tojudge[i].first << " " << tojudge[i].second << " )" << endl;
    }
    cout << "make a square" << endl;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    string s;
    for (int i = 1; i <= 9; i++)
    {
        cin >> s;
        for (int j = 1; j <= 9; j++)
        {
            if (s[j - 1] == '#')
                cord.push_back({i, j});
        }
    }
    int ans = 0;
    for (int i = 0; i < cord.size(); i++)
    {
        for (int j = i + 1; j < cord.size(); j++)
        {
            for (int k = j + 1; k < cord.size(); k++)
            {
                for (int l = k + 1; l < cord.size(); l++)
                {
                    if (issquare({cord[i], cord[j], cord[k], cord[l]}))
                    {
                        // print({cord[i], cord[j], cord[k], cord[l]});
                        ans++;
                    }
                }
            }
        }
    }
    cout << ans;
    return 0;
}

---

D - Yet Another Recursive Function

记忆化搜索可过，因为$n$ 实在是太大了($1e18$)，所以即使是线性复杂度也会超时，由于对于每一个 $x$,其对应的值由 $\lfloor x/3\rfloor$和 $\lfloor x/2\rfloor$决定，这会有很多重复运算的过程。
从正面想，每一个$x$，可以决定 $[x\times 2,x\times 3)$和 $[x\times 3,x\times 4)$ 这两个区间内的元素，所以我们在计算 $f(n)$时候只要将已经求出的值存起来来减少重复计算，这能减少相当的时间

由于数据很大，不能开数组，需要使用map来实现

AC代码

// Problem: D - Yet Another Recursive Function
// Contest: AtCoder - AtCoder Beginner Contest 275
// URL: https://atcoder.jp/contests/abc275/tasks/abc275_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms

#include 
using namespace std;
typedef long long ll;
typedef pair<int, int> pi;
const int N = 2e5 + 10;
const int MOD = 1e9 + 7;
#define endl '\n'
#define PY puts("Yes")
#define PN puts("No")
map<ll, ll> mp;
ll calc(ll x)
{
    if (mp[x])
        return mp[x];
    if (!x)
        return 1;
    return mp[x] = calc(x / 2) + calc(x / 3);
}
int main()
{
    // 1,3,4,7,7,11,11
    ios::sync_with_stdio(false);
    cin.tie(0);
    // f[0] = 1;
    ll n;
    cin >> n;
    cout << calc(n);
    return 0;
}

---

先写到这里有空再更后面的题