RSA加密算法

RSA加密算法：数学魔术背后的安全守护者

RSA加密算法（Rivest-Shamir-Adleman）是一种广泛使用的公钥加密算法，它在信息安全领域具有重要作用。 RSA是由 罗纳德·李维斯特 （Ron Rivest）、 阿迪·萨莫尔 （Adi Shamir）和 伦纳德·阿德曼 （Leonard Adleman）在1977年一起提出的。 当时他们三人都在麻省理工学院工作。 RSA 就是他们三人姓氏开头字母拼在一起组成的。

RSA算法基于数论中的一些重要概念，如大数分解和欧拉函数。它的安全性依赖于大数分解的难度，即从一个大整数的乘积中推导出其因子的困难性。下面是RSA加密算法的基本原理和过程。

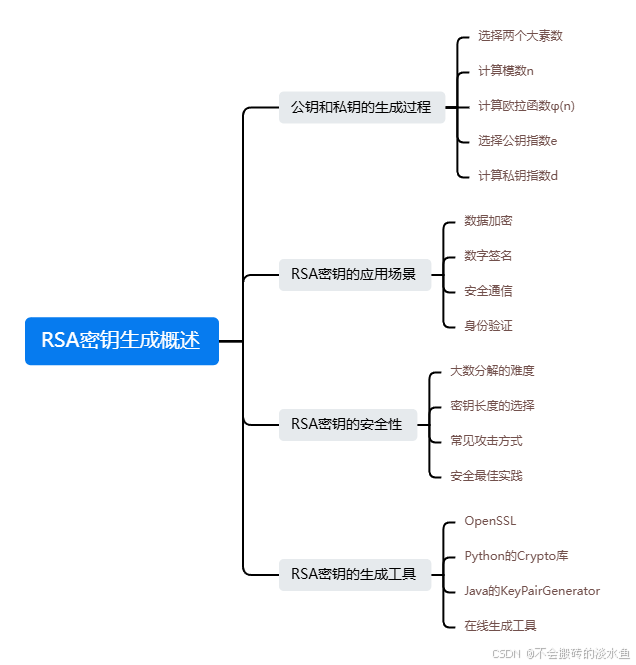
1. 公钥和私钥的生成

RSA加密算法的核心在于生成一对密钥：公钥和私钥。

• 选择两个大素数：首先选择选两个超级大的素数 p 和 q 。

• 计算 n：计算 $n=p\times q$，这个值 n 将作为公钥和私钥的一部分。这个数字 n 在加密和解密过程中非常重要。

• 计算欧拉函数$\varphi (n)$：欧拉函数 $\varphi (n)$ 表示小于 n 且与 n 互质的数的个数。对于$n=p\times q$，有：
  $$\varphi (n)=(p-1)\times (q-1)$$
  参考： $\varphi (n)=n\cdot \left(1-\frac{1}{p_1}\right)\cdot \left(1-\frac{1}{p_2}\right)\cdot \dots \cdot \left(1-\frac{1}{p_k}\right)$

• 选择公钥指数 e：选择一个整数 e ，使得 $\varphi (n)$，并且 e 与 $\varphi (n)$ 互质。通常，选择常用的值，例如 3 或 65537。

• 计算私钥指数 d：通过扩展欧几里得算法计算 d ，使得：
  $$e\times d\equiv 1(\text{mod}\varphi (n))$$
  即 d 是 e 在模 $\varphi (n)$下的逆元。

符号 ≡ 在数学中表示 同余（congruence），它通常用于表示两个数在某个模数下具有相同的余数。
举个例子:
  假设a = 17, b = 5, m = 6。
  可以计算：
   17 ÷ 6 = 2 余5
   5 ÷ 6 = 0 余5
  因此，17 ≡ 5 (mod 6)，因为它们在模6下的余数相同，都是5。

最终，公钥为 (e, n) ，私钥为 (d, n) 。

2. 加密过程

假设发送者使用接收者的公钥加密消息。

• 将消息 M 转换为一个整数 m ，使得 $0\le m<n$。

• 使用公钥 (e, n) 进行加密：
  $$c=m^e(\text{mod}n)$$
  其中 c 是密文。

3. 解密过程

接收者使用私钥进行解密。

• 使用私钥 (d, n) 解密密文 c ：
  $$m=c^d(\text{mod}n)$$
  解密得到的 m 就是原始消息的整数表示，接收者可以将其转换回原始消息 M 。
  下面通过一个简单的例子来展示RSA加密算法的工作原理。为了简化计算，我们将使用较小的数字，但在实际应用中，所使用的数字通常会非常大。

4. 举例

4.1. 选择两个素数 p 和 q

假设我们选择以下两个小素数（实际使用中常达1024位以上）：

• p = 61 （实际中比宇宙原子数还大）
• q = 53

4.2. 计算 n 和 $\varphi (n)$

• 计算 n ：
  $$n=p\times q=61\times 53=3233$$

• 计算欧拉函数 $\varphi (n)$：
  $$\varphi (n)=(p-1)\times (q-1)=(61-1)\times (53-1)=60\times 52=3120$$

4.3. 选择公钥指数 e

我们选择 e = 17(实际中常选择e = 65537) ，它必须满足 1 < e < $\varphi (n)$ 且与 $\varphi (n)$ 互质。显然，17与3120互质。

4.4. 计算私钥指数 d

我们需要找到 d 使得：
$$e\times d\equiv 1(\text{mod}\varphi (n))$$
也就是找到 d ，使得 $17\times d\equiv 1(\text{mod}3120)$。

通过扩展欧几里得算法，我们计算得到：
$$d=2753$$

4.5. 公钥和私钥

现在我们有了公钥和私钥：

• 公钥 (e, n) = (17, 3233)
• 私钥 (d, n) = (2753, 3233)

4.6. 加密过程

假设发送者想要发送消息 “HELLO”，我们先将其转换为数字。例如，将每个字母转换为ASCII值：

• H = 72
• E = 69
• L = 76
• L = 76
• O = 79

因此，消息 “HELLO” 可以表示为数字序列 ( 72, 69, 76, 76, 79 )。

我们选择加密第一个字母 m = 72 ：

使用公钥 (e, n) = (17, 3233) 进行加密：
$$c=m^e(\text{mod}n)=72^{17}(\text{mod}3233)$$

计算得到：
$$c=72^{17}(\text{mod}3233)=2201$$

所以，字母 “H” 的加密密文是 2201。

4.7. 解密过程

接收者使用私钥 (d, n) = (2753, 3233) 来解密密文 c = 2201 。

使用私钥进行解密：
$$m=c^d(\text{mod}n)=2201^{2753}(\text{mod}3233)$$

计算得到：
$$m=2201^{2753}(\text{mod}3233)=72$$

接收者得到的结果是 72，这正是字母 “H” 的ASCII值。

4.8. 解密其他字母

同样的方法可以用于解密其他字母。通过公钥加密和私钥解密，接收者可以还原完整的消息。

5. ️RSA算法的安全性

RSA算法的安全性基于大数分解的困难性。具体来说，给定一个大的 n 和公钥 e ，很难从密文 c 直接计算出原始消息 m 。RSA的安全性依赖于 n 的因子化问题，即从 $n=p\times q$ 中恢复出 p 和 q 是非常困难的，特别是当 p 和 q 是非常大的素数时。

6. ⚖️RSA的优缺点

优点：

• 非常安全：RSA依赖于大数分解问题的困难性，目前没有有效的解法。
• 公钥加密：用户可以公开公钥，只要保持私钥的安全性，任何人都可以加密消息，只有私钥拥有者可以解密。

缺点：

• 计算量大：RSA加密和解密的计算量相对较大，尤其是对于非常大的密钥。对于较长的消息，通常需要使用对称加密算法（如AES）进行加密，RSA用于加密对称密钥。
• 密钥管理：密钥的生成和管理非常重要，公钥需要公开，私钥需要保密。对于大规模系统，密钥的管理可能比较复杂。

7. RSA的应用

• 数据加密：RSA可用于对敏感数据的加密保护。
• 数字签名：RSA可以用来生成数字签名，验证消息的完整性和发送者的身份。
• SSL/TLS协议：RSA是SSL/TLS协议中的核心算法之一，用于加密通信中的密钥交换。

总结来说，RSA加密算法是基于数论的公钥加密算法，通过大数分解的困难性提供安全性，广泛应用于数字通信和网络安全中。

参考文献：

[1] https://zh.wikipedia.org/zh-cn/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95
[2] Rivest R L , Shamir A , Adleman L .A method for obtaining digital signatures and public-key cryptosystems[J].Communications of the Acm, 1978, 21(2):120-126.DOI:10.1145/359340.359342.