HDU 4069 Squiggly Sudoku（DLX）（The 36th ACM/ICPC Asia Regional Fuzhou Site —— Online Contest）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4069

Problem Description

Today we play a squiggly  sudoku, The objective is to fill a 9*9 grid with digits so that each column, each row, and each of the nine Connecting-sub-grids that compose the grid contains all of the digits from 1 to 9.
Left figure is the puzzle and right figure is one solution.

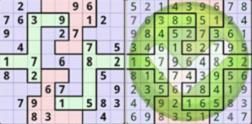
Now, give you the information of the puzzle, please tell me is there no solution or multiple solution or one solution.

 

Input

The first line is a number T(1<=T<=2500), represents the number of case. The next T blocks follow each indicates a case.
Each case contains nine lines, Each line contains nine integers.
Each module number tells the information of the gird and is the sum of up to five integers:
0~9: '0' means this gird is empty, '1' - '9' means the gird is already filled in.
16: wall to the up
32: wall to the right
64: wall to the down
128: wall to the left
I promise there must be nine Connecting-sub-grids, and each contains nine girds.

 

Output

For each case, if there are Multiple Solutions or no solution just output "Multiple Solutions" or "No solution". Else output the exclusive solution.(as shown in the sample output)

 

题目大意：给一个不规则的9阶数独，问是否有唯一解，是则输出。

思路：先DFS一下，找出每个格子对应的块号，再套DLX的模板。

 

代码（1203MS）：

  1 #include <iostream>

  2 #include <cstdio>

  3 #include <algorithm>

  4 #include <cstring>

  5 #include <vector>

  6 using namespace std;

  7 typedef long long LL;

  8 

  9 const int MAXN = 10;

 10 const int MAXC = 9 * 9 * 4 + 10;

 11 const int MAXR = 9 * 9 * 9 + 10;

 12 const int MAXP = MAXR * 4 + MAXC;

 13 

 14 struct DLX {

 15     int sz;

 16     int sum[MAXC];

 17     int row[MAXP], col[MAXP];

 18     int left[MAXP], right[MAXP], up[MAXP], down[MAXP];

 19     int ansd, ans[MAXR], anscnt;

 20 

 21     void init(int n) {

 22         for(int i = 0; i <= n; ++i) {

 23             up[i] = down[i] = i;

 24             left[i] = i - 1; right[i] = i + 1;

 25         }

 26         left[0] = n; right[n] = 0;

 27         sz = n + 1;

 28         memset(sum, 0, sizeof(sum));

 29     }

 30 

 31     void add_row(int r, vector<int> &func) {

 32         int first = sz;

 33         for(size_t i = 0; i < func.size(); ++i) {

 34             int c = func[i];

 35             left[sz] = sz - 1; right[sz] = sz + 1; up[sz] = up[c]; down[sz] = c;

 36             down[up[c]] = sz; up[c] = sz;

 37             row[sz] = r; col[sz] = c;

 38             ++sum[c], ++sz;

 39         }

 40         left[first] = sz - 1; right[sz - 1] = first;

 41     }

 42 

 43     void remove(int c) {

 44         left[right[c]] = left[c];

 45         right[left[c]] = right[c];

 46         for(int i = down[c]; i != c; i = down[i]) {

 47             for(int j = right[i]; j != i; j = right[j])

 48                 up[down[j]] = up[j], down[up[j]] = down[j], --sum[col[j]];

 49         }

 50     }

 51 

 52     void restore(int c) {

 53         for(int i = up[c]; i != c; i = up[i]) {

 54             for(int j = left[i]; j != i; j = left[j])

 55                 up[down[j]] = j, down[up[j]] = j, ++sum[col[j]];

 56         }

 57         left[right[c]] = c;

 58         right[left[c]] = c;

 59     }

 60 

 61     bool dfs(int d) {

 62         if(!right[0]) {

 63             ansd = d;

 64             return ++anscnt == 2;

 65         }

 66         int c = right[0];

 67         for(int i = right[0]; i != 0; i = right[i]) if(sum[i] < sum[c]) c = i;

 68         remove(c);

 69         for(int i = down[c]; i != c; i = down[i]) {

 70             if(!anscnt) ans[d] = row[i];

 71             for(int j = right[i]; j != i; j = right[j]) remove(col[j]);

 72             if(dfs(d + 1)) return true;

 73             for(int j = left[i]; j != i; j = left[j]) restore(col[j]);

 74         }

 75         restore(c);

 76         return false;

 77     }

 78 

 79     int solve(vector<int> &v) {

 80         v.clear();

 81         anscnt = 0;

 82         dfs(0);

 83         if(anscnt == 1) for(int i = 0; i < ansd; ++i) v.push_back(ans[i]);

 84         return anscnt;

 85     }

 86 } solver;

 87 

 88 const int SLOT = 0;

 89 const int ROW = 1;

 90 const int COL = 2;

 91 const int SUB = 3;

 92 

 93 int fr[] = {-1, 0, 1, 0};

 94 int fc[] = {0, 1, 0, -1};

 95 int fp[] = {16, 32, 64, 128};

 96 

 97 int mat[MAXN][MAXN];

 98 int val[MAXN][MAXN], cnt;

 99 int T, n = 9;

100 

101 bool in_n(int x) {

102     return 0 <= x && x < n;

103 }

104 

105 void dfs(int r, int c, int p) {

106     val[r][c] = p;

107     for(int i = 0; i < 4; ++i) {

108         int nr = r + fr[i], nc = c + fc[i];

109         if(in_n(nr) && in_n(nc) && ((fp[i] & mat[r][c]) == 0) && !val[nr][nc])

110             dfs(nr, nc, p);

111     }

112 }

113 

114 void print(int mat[MAXN][MAXN]) {

115     for(int i = 0; i < n; ++i) {

116         for(int j = 0; j < n; ++j) printf("%d", mat[i][j]);

117         puts("");

118     }

119 }

120 

121 int encode(int a, int b, int c) {

122     return a * 81 + b * 9 + c + 1;

123 }

124 

125 void decode(int code, int &a, int &b, int &c) {

126     --code;

127     c = code % 9; code /= 9;

128     b = code % 9; code /= 9;

129     a = code;

130 }

131 

132 int main() {

133     scanf("%d", &T);

134     for(int kase = 1; kase <= T; ++kase) {

135         for(int i = 0; i < n; ++i)

136             for(int j = 0; j < n; ++j) scanf("%d", &mat[i][j]);

137         memset(val, 0, sizeof(val));

138         cnt = 0;

139         for(int i = 0; i < n; ++i)

140             for(int j = 0; j < n; ++j) if(!val[i][j]) dfs(i, j, ++cnt);

141         printf("Case %d:\n", kase);

142         //print(val);

143         solver.init(9 * 9 * 4);

144         for(int r = 0; r < n; ++r)

145             for(int c = 0; c < n; ++c)

146                 for(int i = 0; i < 4; ++i) mat[r][c] &= ~fp[i];

147         //print(mat);

148         for(int r = 0; r < n; ++r) for(int c = 0; c < n; ++c) for(int v = 0; v < n; ++v) {

149             if(!mat[r][c] || mat[r][c] == 1 + v) {

150                 vector<int> func;

151                 func.push_back(encode(SLOT, r, c));

152                 func.push_back(encode(ROW, r, v));

153                 func.push_back(encode(COL, c, v));

154                 func.push_back(encode(SUB, val[r][c] - 1, v));

155                 solver.add_row(encode(r, c, v), func);

156             }

157         }

158         vector<int> ans;

159         int res = solver.solve(ans);

160         if(res == 0) puts("No solution");

161         if(res == 1) {

162             int r, c, v;

163             for(size_t i = 0; i < ans.size(); ++i) {

164                 decode(ans[i], r, c, v);

165                 mat[r][c] = 1 + v;

166             }

167             print(mat);

168         }

169         if(res == 2) puts("Multiple Solutions");

170     }

171 }

View Code